【Open AI】Large Language Monkeys- Scaling Inference Compute with Repeated Sampling 大型语言猴子：重复采样以扩展推理计算

这篇论文探讨了在语言模型推理过程中增加样本数量以提高覆盖范围的方法。作者通过多个任务和模型的研究发现，在自动验证领域中，随着样本数量的增加，问题解决率也相应地提高。例如，在SWE-bench Lite中使用DeepSeek-V2-Coder-Instruct模型进行重复采样，可以将解决问题的比例从15.9%提高到56%，超过了单次尝试的最先进方法。此外，作者还发现了关于采样数量与覆盖范围之间存在指

禅与计算机程序设计艺术

1701人浏览 · 2024-09-15 10:16:40

禅与计算机程序设计艺术 · 2024-09-15 10:16:40 发布

摘要

figure_1

论文速读

论文方法

方法描述

本文主要研究了如何通过重复采样来提高模型在不同任务上的表现。具体来说，作者考虑了五个不同的任务：GSM8K、MATH、MiniF2F-MATH、CodeContests和SWE-bench Lite，并针对每个任务设计了一种自动验证方法，以确保模型生成的候选解决方案是正确的。作者使用了不同的预训练模型（如Llama-3-8B-Instruct、Llama-3-70B-Instruct、Gemma-2B、Gemma-7B和Pythia）以及不同的样本预算来进行实验，并观察到随着样本数量的增加，模型的覆盖范围也随之增加。

方法改进

本文的主要贡献在于提出了重复采样的方法，并证明了这种方法可以显著提高模型的表现。具体来说，作者使用了多次独立的采样过程来生成多个候选解决方案，并根据这些方案的正确性来计算模型的成功率。此外，作者还针对不同的任务设计了不同的自动验证方法，以便更好地评估模型的表现。

解决的问题

本文的研究旨在解决机器学习模型在处理复杂问题时所面临的挑战。具体来说，作者关注的是那些需要生成正确答案的任务，例如数学问题、编程问题等。传统的单次采样方法往往无法保证生成的候选解决方案是正确的，因此难以获得可靠的结果。而本文提出的重复采样方法则可以通过多次独立的采样过程来生成更多的正确答案，从而提高了模型的表现。

figure_2

figure_3

论文实验

本文主要介绍了在自然语言处理和软件开发任务中，重复采样（repeated sampling）的应用及其效果，并通过一系列对比实验来验证其有效性。具体来说，文章分为以下几个部分：

重复采样的概念与优势：首先，文章介绍了什么是重复采样以及它在提高模型性能方面的优势。例如，在解决编程问题时，使用较弱的模型多次采样可以比单次采样更有效率。
重复采样在不同任务中的表现：接着，文章通过对 MiniF2F、CodeContests、MATH 和 GSM8K 四个任务的数据分析，展示了重复采样在不同任务中的表现差异。例如，在 GSM8K 和 MATH 上，使用较小的模型（Llama-3-8B-Instruct）反复采样可以获得更高的覆盖率，而在 CodeContests 上则需要更大的模型（Llama-3-70B-Instruct）才能取得更好的效果。
基于复杂数学公式的关系：然后，文章基于数学关系对重复采样进行了建模，并提出了一个幂律函数来描述覆盖面积与样本数量之间的关系。此外，文章还发现，对于同一类别的模型，在相同任务上的覆盖曲线具有相似的斜率，但不同的水平偏移量。
精度和可靠性的问题：最后，文章讨论了重复采样面临的精度和可靠性问题。例如，在 GSM8K 和 MATH 上，正确的解决方案可能只占总样本数的一小部分，因此如何识别出这些正确方案是一个挑战。此外，文章还提到了一些关于软件开发任务中测试工具不完善所导致的问题，如测试结果不稳定和假阴性等。

总的来说，本文通过多个实验数据和案例，论证了重复采样在不同任务中的应用价值，并指出了其中存在的精度和可靠性问题。这对于研究人员和开发者来说都是有参考意义的。

table_1

table_2

论文总结

文章优点

本文提出了重复采样这一新的计算模型，用于在推理时提高模型性能。通过实验证明，在多个任务和模型中，重复采样可以显著提高解决问题的能力，并且当正确解决方案能够被自动验证工具或其他验证算法识别时，重复采样可以在推理过程中放大模型能力。此外，文章还探讨了如何改进重复采样的效果，包括增加样本多样性、引入多轮交互以及学习之前的尝试等方向。

方法创新点

本文提出的方法是基于重复采样的，这是一种不同于聊天机器人请求的推理工作负载。与生产环境中的聊天机器人部署相比，重复采样更注重整体吞吐量和最大化硬件利用率，而不是低延迟响应。因此，使用重复采样可以在更低的成本下完成推断任务，进一步促进选择使用较少次数但较便宜的模型来代替更多的次但更昂贵的模型。

未来展望

该文提出的方法为解决一些现有问题提供了新思路，例如缺乏自动验证的问题。然而，目前仍需要开发更强大的验证器以实现更广泛的应用。此外，作者还提到了一些可能的方向，如设计将非结构化任务转化为可验证的任务的转换器。这些研究可能会在未来的研究中得到应用和发展。

2024年7月30日

摘要

通过增加用于训练语言模型的计算量，其能力得到了显著提高。然而，在推理方面，我们通常只允许每个问题进行一次尝试。在这里，我们将探索推理计算作为另一个扩展轴，通过增加生成样本的数量来实现。在多个任务和模型上，我们观察到覆盖率——任何尝试解决的问题比例——随着样本数量的增长而呈指数级增长。在像编程和正式证明这样的领域中，所有答案都可以自动验证，这些增加的覆盖率直接转化为性能改进。当我们在SWE-bench Lite上应用重复采样时，使用DeepSeek-V2-Coder-Instruct的覆盖率从一个样本中的15.9％增加到250个样本中的56％，超过了单次尝试的最佳状态（43％），该最佳状态使用了更强大的前沿模型。此外，使用当前API定价，用五个样本放大便宜的DeepSeek模型比支付GPT-4o或Claude 3.5 Sonnet的一个样本的溢价更具成本效益，并且解决了更多的问题。有趣的是，覆盖率与样本数之间的关系往往呈对数线性关系，并可以用幂律指数化来建模，这表明存在推理时间缩放定律。最后，我们发现识别出许多世代中的正确样本仍然是没有自动验证器领域的未来研究的重要方向。在解决来自GSM8K和MATH的数学文字问题时，Llama-3模型的覆盖率在1万个样本时达到超过95％。然而，常见的从样本集合中选择正确解决方案的方法，如多数投票或奖励模型，在几百个样本后就会停滞不前，并无法完全随样本预算扩展。

1.介绍

大语言模型 (LLM) 解决编码、数学和其他推理任务的能力在过去几年中有了显著提高 [42，11]。扩大模型训练规模一直是这些收益的一致驱动因素。对更大模型的投资、更大的预训练数据集和更广泛的后训练投资（例如通过收集人类偏好标签）导致了非常有能力的通用系统 [2，3，4，47] 。

第 2 页

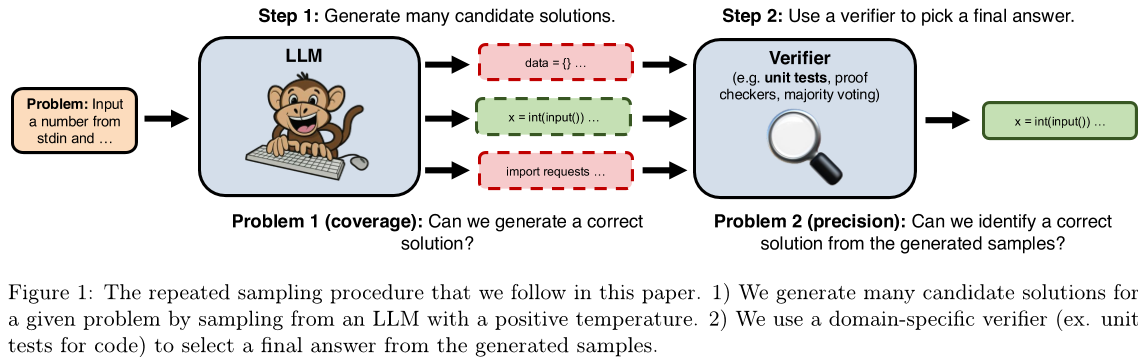
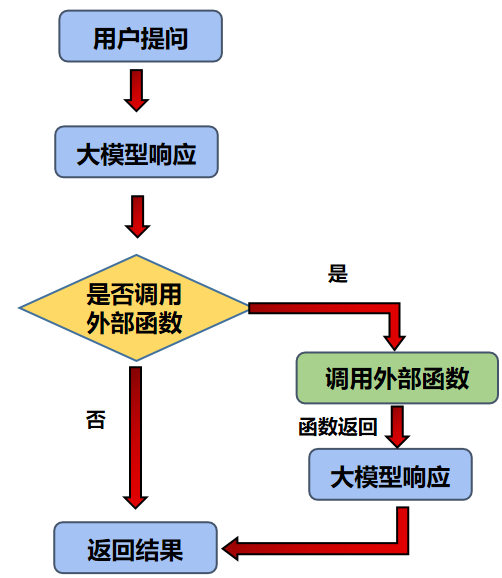
相比之下，用于推理的计算量规模有限。较大的模型确实需要比较小的模型更多的推理计算，并且提示技术（如链式思维）可以提高答案质量，但代价是更长的输出（因此更昂贵）。然而，在与LLM交互时，用户和开发人员通常会限制模型仅在解决一个问题时进行一次尝试。在这项工作中，我们研究重复采样（图1所示）作为扩展推理计算的替代轴来改善LLM推理性能。

重复抽样的有效性取决于两个关键属性：

覆盖范围：随着样本数量的增加，我们能用任何生成的样本解决多少问题？

精度：在我们必须从生成的样本集合中选择最终答案的情况下，我们可以识别出正确的样本吗？

无限次尝试，任何将每个序列分配非零概率的模型都将实现完美的覆盖。然而，重复采样只有在我们能够通过可行预算提高覆盖率时才具有实际意义。此外，在没有决定样本之间差异的能力的情况下，重复采样的应用是有限的。现有工作提供了这两个方向上的鼓舞人心的证据，显示了重复采样在数学、编码和解谜场景中改善性能的例子 [55, 43, 22] 。值得注意的是，AlphaCode 是一种最先进的竞争编程系统，发现每道题一千万个样本可以继续提高性能。

在这里，我们展示重复采样是一种有效的方法，在一系列任务、模型和样本预算中提高覆盖范围。例如，当使用Gemma-2B[48]解决CodeContests[37]编程问题时，随着样本数量的增加（从一次尝试中的0.02％到10,000次尝试中的7.1％），覆盖率增加了超过300倍。有趣的是，log (覆盖率) 和样本数之间的关系通常遵循一个近似幂律。在Llama-3[3]和Gemma模型上，我们观察到随着样本数量的增加，覆盖率以近乎对数线性的方式增长几个数量级。

在所有模型解决方案都可以自动验证的环境中，例如使用证明检查器或单元测试，这些覆盖率增加直接转化为改进的任务性能。当应用于竞争性编程和编写Lean证明时，像Llama-3-8B-Instruct这样的模型可以超过单次尝试表现更强的GPT-4o[2]。这种放大较弱模型的能力也扩展到GitHub问题的真实生活SWE-bench Lite数据集，其中当前单次尝试状态的最新技术（SOTA），由 |

第 3 页

混合了GPT-4o和Claude 3.5 Sonnet模型的DeepSeek-Coder-V2-Instruct在基准测试中仅达到15.9%，而通过将尝试次数增加到250次，我们解决了问题的比例达到了56%，超过了单次尝试的最佳水平。

除了提高模型质量外，重复采样还提供了一种新的机制来最小化LLM推理成本。当保持总推理FLOPS数量不变时，我们发现，在某些数据集（例如MATH）中，使用较小的模型和更多的尝试可以达到最大的覆盖范围，而在其他数据集（例如CodeContests）中，则应使用较大的模型。此外，我们在解决SWE-bench Lite问题的情况下比较了DeepSeek-V2-Coder-Instruct、GPT-4o和Claude Sonnet 3.5的API价格。在保持代理框架（Moatless Tools [62]）不变的情况下，从较弱且更便宜的DeepSeek模型中抽取五次比单次尝试从Claude或GPT中解决更多问题，并且也比后者便宜超过三倍。

最后，在数学文字问题设置中，答案不能由现有工具自动验证，我们发现覆盖范围和常见方法的性能之间存在很大的差距。在使用Llama-3-8B-Instruct解决MATH[24]问题时，覆盖率从100个样本中的79.8％增加到10,000个样本中的95.3％。然而，诸如多数投票法和使用奖励模型的方法在较低的样本预算下达到上限，并且仅在相同范围内从38.7％扩展到39.8％。这些结果表明构建稳健的验证器仍然是一个开放的问题。

总之，我们的主要观察结果是：

我们证明，通过重复采样进行推理计算的缩放导致在各种任务、模型和样本预算上覆盖范围大幅提高。这使得可能，并且有时成本效益更高，可以放大许多样本的较弱模型并超过更强大模型的一次尝试。值得注意的是，我们能够从DeepSeek-V2-Coder-Instruct中抽取250次来解决SWE-bench Lite中的56％的问题，超过了单次尝试的SOTA为43％。

我们表明，覆盖与样本数量之间的关系通常可以使用指数幂律进行建模，这暗示了在推断时计算的缩放定律的形式。

在没有自动验证器的域中，我们表明，像多数投票和奖励模型评分这样的验证方法在大约100个样本时达到上限。这导致了这些方法实现性能与覆盖范围上界之间的差距越来越大。

2.重复抽样扩展

我们关注的是通过或失败的任务，其中候选解决方案可以被评分正确或错误。这些任务的主要兴趣指标是成功率：我们能够解决的问题的百分比。在重复采样中，我们考虑一个模型可以生成许多候选解决方案以尝试解决问题的情况。因此，成功率不仅受到产生许多问题的正确样本的能力（即覆盖范围）的影响，而且还受到识别这些正确样本的能力（即精度）。

精确问题的难度取决于样本验证工具的可用性。在Lean中证明正式陈述时，证明检查器可以快速确定候选解决方案是否正确。同样，单元测试也可以用于验证编码任务中的候选解决方案。

第 4 页

在这些情况下，精度会自动处理，并且提高覆盖范围直接转化为更高的成功率。相比之下，用于验证来自GSM8K和MATH的数学文字问题解决方案的工具有限，需要额外的验证方法来决定从许多（通常相互矛盾）样本中选择唯一的最终答案。

我们考虑以下五个任务：

1.GSM8K：一个小学数学问题的语料库。我们对GSM8K测试集中的随机子集（128个问题）进行评估。

2.MATH：另一个比GSM8K[13]更难的数学问题数据集。同样，我们从这个数据集测试集中随机抽取了128个问题进行评估。

MiniF2F-MATH：一个数学问题的集合，这些数学问题已经被正式化为证明检查语言。我们使用Lean4作为我们的语言，并在从MATH数据集中形式化的130个测试集问题上进行评估。

4.CodeContests：一个竞争性编程问题的数据集[37]。每个问题都有文本描述，以及一组输入输出测试用例（隐藏在模型中），可以用来验证候选解决方案的正确性。我们强制要求模型使用Python3编写其解决方案。

5.SWE-bench Lite：一个由Github问题构成的现实世界数据集，每个问题都包含描述和代码库快照。要解决一个问题，模型必须编辑代码库中的文件（在我们使用的SWE-bench Lite子集中，只需要修改单个文件）。候选解决方案可以使用代码库的单元测试套件自动检查。

在这些任务中，MiniF2F-MATH、CodeContests和SWE-bench Lite具有自动验证器（形式为Lean4证明检查器、测试用例和单元测试套件）。我们首先研究重复采样如何提高模型覆盖率。覆盖率的改进直接对应于带有自动验证器的任务的成功率增加，并且在一般情况下提供成功概率的上限。在编码设置中，我们的覆盖率定义与常用通过@k指标等价[15]，其中k表示每个问题的样本数。我们在评估CodeContests和SWE-bench Lite时直接使用该指标。对于MiniF2F，该指标类似，根据Lean4证明检查器来定义“通过”。对于GSM8K和MATH，覆盖率对应于使用oracle验证器，它检查输出是否正确最终答案以确定任何样本是否“通过”。为了减少计算覆盖率时的方差，我们采用Chen等人提出的无偏估计公式[15]。在每次实验中，我们首先对每个问题索引i生成N个样本，并计算正确的样本数量Ci。然后根据k≤N感兴趣的所有k值计算通过@k分数：

我们使用了Chen等人[15]中建议的上述公式中的数值稳定实现。结果和代码将在https://scalyresearch.stanford.edu/pubs/large_language_monkeys/ 上提供。

第 5 页

SWE-bench Lite

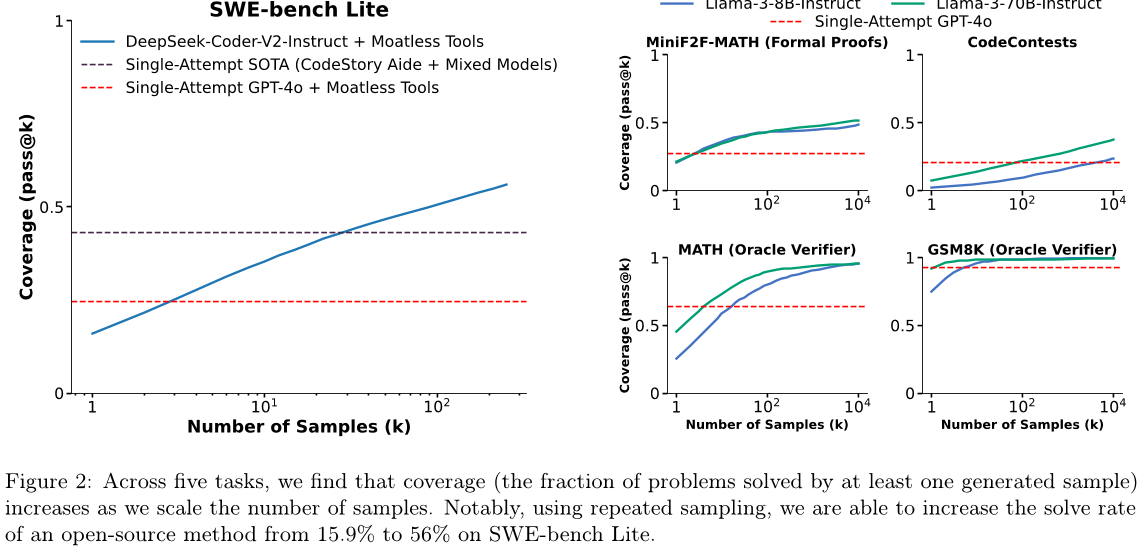
图2：在五个任务中，我们发现覆盖率（至少有一个生成样本解决的问题比例）随着样本数量的增加而增加。值得注意的是，在使用重复采样时，我们可以将开源方法SWE-bench Lite的解决率从15.9％提高到56％。

2.1 在任务中重复采样是有效的。

在这里，我们证明了重复采样可以提高多个任务和一系列样本预算的覆盖范围。我们评估Llama-3-8B-Instruct和Llama-3-70B-Instruct在CodeContests、MiniF2F、GSM8K和MATH上生成10,000个独立样本，每个问题。对于SWE-bench Lite，我们使用DeepSeek-V2-Coder-Instruct[19]，因为此任务所需的上下文长度超过了Llama-3模型的限制。如解决SWE-bench问题的标准一样，我们在我们的LLM中配备了一个软件框架，为模型提供导航代码库并编辑工具。在我们的工作中，我们使用开源Moatless Tools库[62]。请注意，解决一个SWE-bench问题需要LLM与Moatless Tools之间进行来回交换。这个基准的一个样本/尝试是指整个多轮轨迹。为了降低成本，我们限制每个问题的尝试次数为250次，所有尝试都是相互独立的。

我们在图2中报告了我们的结果。我们还包括了GPT-4o在每个任务上的单次尝试性能，以及SWE-bench Lite的单次尝试最佳性能（CodeStory Aide[1]使用了GPT-4o和Claude 3.5 Sonnet的组合）。在所有五个任务上，我们发现覆盖率随着样本预算的增加而平稳地提高。当所有LLM都只进行一次尝试时，在每个任务上，GPT-4o的表现均优于Llama和DeepSeek模型。然而，随着样本数量的增加，这三个较弱的模型的单次尝试性能超过了GPT-4o。对于SWE-bench Lite，我们解决了56％的问题，超过了单次尝试的最佳性能43％。

2.2 反复采样在模型大小和家族中都是有效的。

Section 2.1的结果表明，重复采样可以提高覆盖范围。然而，我们仅展示了三种最近的、经过指令调优的模型（参数量为8B或更多）的趋势。现在，我们证明了这些趋势在其他模型大小、家族和后训练水平上仍然成立。我们将我们的评估扩展到包括更广泛的模型集：

• Llama 3：Llama-3-8B，Llama-3-8B-Instruct，Llama-3-70B-Instruct。

• Gemma：Gemma-2B，Gemma-7B [48]。

第 6 页

Llama-3-8B Llama-3-8B-Instruct Llama-3-70B-Instruct Gemma-2B Gemma-7B

•Pythia：通过Pythia-70M到Pythia-12B（总共8个模型）[9]。

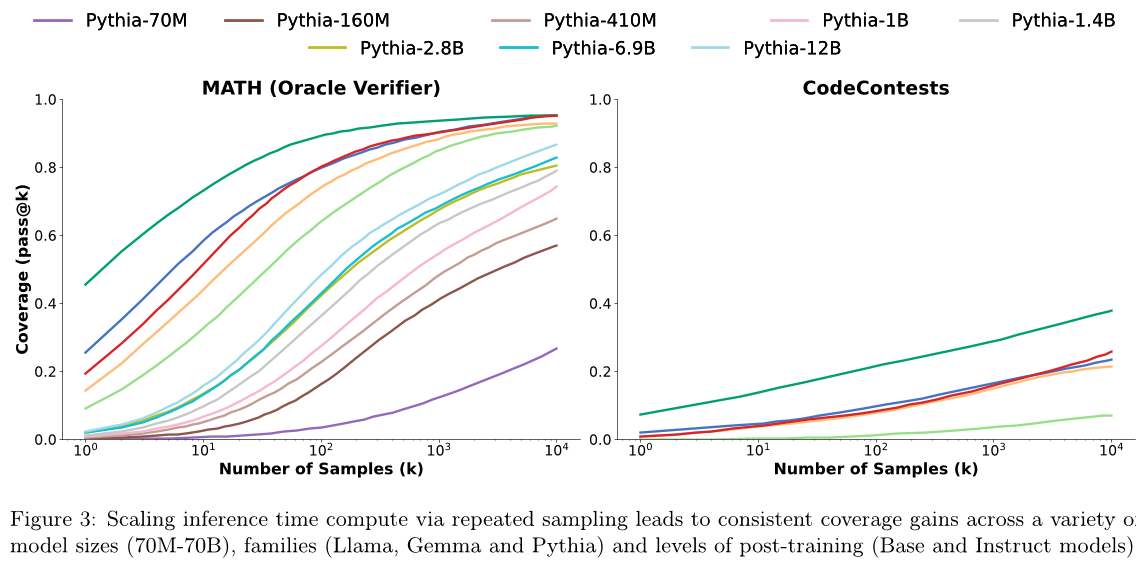
我们限制评估到 MATH 和 CodeContests 数据集，以最小化推理成本，并在图 3 中报告结果。几乎每个模型的覆盖范围都有所增加，较小的模型在重复采样时表现出一些最明显的覆盖范围增加。在 CodeContests 上，Gemma-2B 的覆盖范围增加了超过 300 倍，从通过率 @1 为 0.02% 到通过率 @10K 为 7.1%。同样，在使用 Pythia-160M 解决 MATH 问题时，覆盖范围从通过率 @1 为 0.27% 增加到通过率 @10K 为 57%。

这种模式的例外是，Pythia家族在CodeContests上评估时。所有Pythia模型在这个数据集上的覆盖率都为零，即使样本预算为10,000个样本。我们推测这可能是因为Pythia被训练在比Llama和Gemma更少的编码特定的数据上。

2.3 反复采样有助于平衡性能和成本

从第2.1节和第2.2节的结果中得出的一个重要结论是，重复采样使较弱模型的能力得以放大，并且可以超过单个样本的较强模型。在这里，我们证明了这种放大比使用更强、更昂贵的模型更加经济有效，为从业者在试图同时优化性能和成本时提供了一种新的自由度。

我们首先将FLOPS作为成本指标，分析第2节中的Llama-3结果。我们将图2的结果重新绘制，现在以总推理FLOPS为变量而不是样本预算来可视化覆盖范围。由于Llama-3模型是密集的变压器，在矩阵乘法中大多数参数被使用，我们用公式近似推理FLOPS：

每个令牌的FLOPS≈2∗（参数数+2∗层数×令牌维度×上下文长度）总推理FLOPS≈提示令牌数×每个令牌的FLOPS+解码令牌数×每个令牌的FLOPS×完成次数

第 7 页

我们在图4中展示了我们对MiniF2F、CodeContests、MATH和GSM8K的重新缩放结果。有趣的是，覆盖范围最大的模型随计算预算和任务而变化。在MiniF2F、GSM8K和MATH上，当固定FLOP预算时，Llama-3-8B-Instruct总是比更大的（且更昂贵）的70B模型具有更高的覆盖率。然而，在CodeContests上，70B模型几乎总是更具成本效益。值得注意的是，仅查看FLOPs可能会是一个粗略的成本度量标准，它忽略了系统效率的其他方面[20]。特别是重复采样可以利用大批次大小和专门优化，这些优化提高了系统的吞吐量相对于单次尝试推理工作负载[32, 6, 61]。我们在第5节详细讨论了这一点。

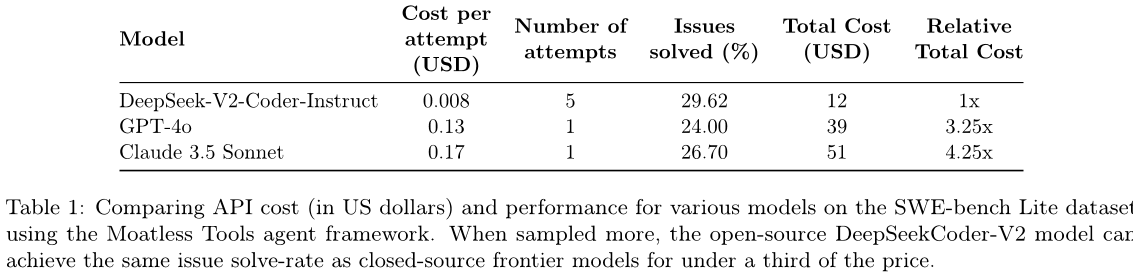
我们还研究了解决SWE-bench Lite问题时重复采样的美元成本，使用当前API定价。保持代理框架（Moatless Tools）不变，我们考虑对每个问题分别使用Claude 3.5 Sonnet和GPT-4o进行一次尝试，并且使用DeepSeek-V2-Coder-Instruct进行重复采样。我们在表1中报告了每种方法的平均成本和问题解决率。虽然DeepSeek模型不如GPT和Claude模型强大，但它也比这些模型便宜超过10倍。在这种情况下，重复采样提供了一种更便宜的选择，以支付访问强模型的溢价，同时实现更高的问题解决率。

3. 描述重复抽样的好处。

有关大型语言模型 (LLM) 的损失与训练计算之间的关系，已经通过训练缩放定律进行了很好的刻画 [25、33、26]。这些定律在许多数量级上都得到了验证，并且激励了模型开发人员对大规模投资进行训练的信心。受此启发

第 8 页

通过训练规模定律，我们旨在更好地刻画覆盖范围与样本预算（即推理计算量）之间的关系，并提出两个有趣观察：

覆盖率与样本数量之间的关系通常可以用幂指数模型表示。

对于给定的任务，来自同一族的不同模型的覆盖曲线类似于具有相似斜率但水平偏移不同的S型曲线。

3.1 反复抽样中的幂律

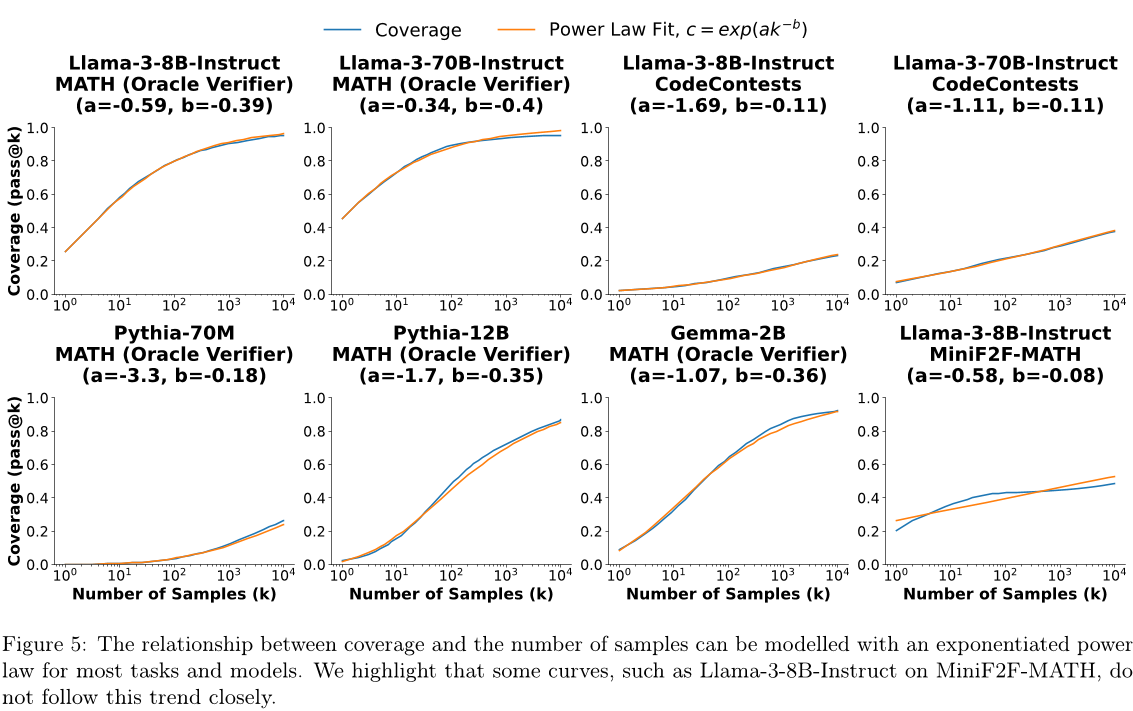
在这里，我们开发了一个明确的模型来描述覆盖范围和样本数量之间的关系。GPT-4技术报告[41]发现，一个模型在编码问题上的平均对数通过率与其训练计算量之间可以用幂律很好地建模。我们首先采用相同的函数类，但现在将对数覆盖c作为样本数量k的函数进行建模：

其中，a和b是拟合模型参数。为了直接预测覆盖范围，我们对两边进行指数运算，最终得到的模型为：

我们在图5中提供了拟合覆盖曲线的示例，并在附录C.2中提供了其他曲线。虽然这些定律不如训练缩放定律精确（特别是在MiniF2F-MATH上），但它们提供了一些令人鼓舞的早期证据，表明推理缩放的好处可以被刻画出来。

第 9 页

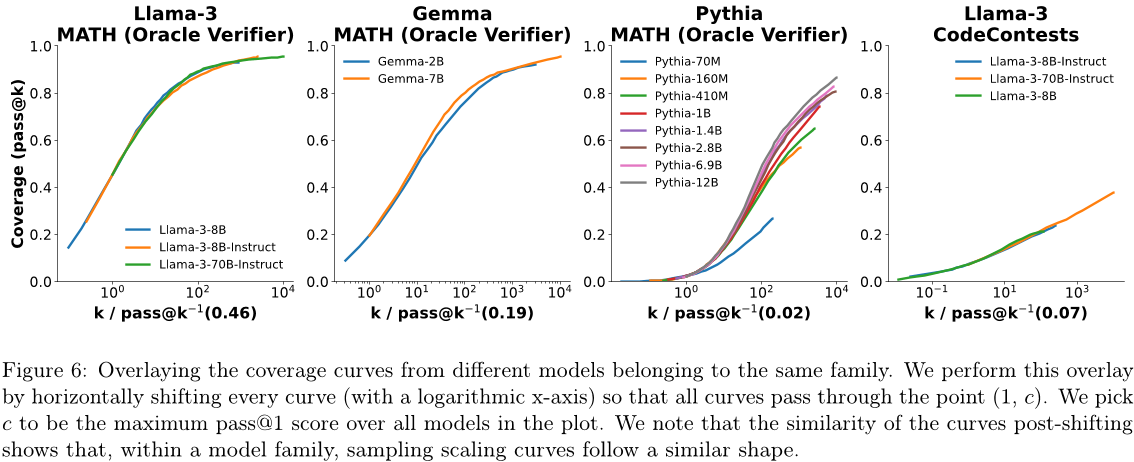
3.2 模型覆盖曲线的相似性

有趣的是，当比较同一任务上来自同一族的不同模型的覆盖曲线（x轴为对数坐标）时（见图3），似乎追踪S型曲线具有相同的斜率，但独特的水平偏移。为了进一步研究这一点，我们在图6中叠加了不同模型来自同一族的覆盖曲线。我们通过选择一个锚定的覆盖率值c，并将每个曲线向左移动（在对数空间中），使得每个曲线都经过点（1，c）。这对应于以log (pass@k-1(c)) 向左移动，其中pass@k-1(c)表示所有模型来自同一家族的最大自然数k，使得pass@k = c。我们将c设置为所有模型来自同一家族的最大pass@1得分。这些相似性表明，在同一族中的模型之间，从c到cc所需的增加的对数样本预算（或等效地，样本预算的乘法增加）来提高覆盖率是大约恒定的。

重复抽样需要精确度。

到目前为止，我们已经专注于测量模型覆盖范围，并在可以始终识别正确模型样本的最佳情况下，描述重复采样的好处。现在我们将转向精度的互补问题：给定一组模型样本，我们可以识别正确的吗？在第4.1节中，我们在GSM8K和MATH上评估了两种常见的验证方法（多数投票和奖励模型评分）。此外，在第4.2节中，我们讨论了依赖单元测试来识别正确软件程序时可能存在的陷阱。

4.1 公共验证方法并不总是与样本预算成比例。

我们评估的五个任务中，只有GSM8K和MATH没有自动验证解决方案的工具。在这里，我们评估了决定最终答案的两种常见方法：在样本之间计算多数投票，并使用奖励模型为每个样本分配分数。我们在第2节中生成了Llama-3-8B-Instruct和Llama-3-70B-Instruct的10,000个样本上测试这些技术，以识别正确的解决方案。我们基准测试三种方法：

多数投票：我们选择最常见最终答案[55]。

第 10 页

多数投票奖励模型 + 最佳的N个奖励模型 + 多数投票覆盖率（通过@k）

奖励模型 + 最佳的N：我们使用奖励模型 [17] 来为每个解决方案打分，并从得分最高的样本中选择答案。

奖励模型 + 多数投票：我们计算一个多数投票，其中每个样本的权重由其奖励模型得分决定。

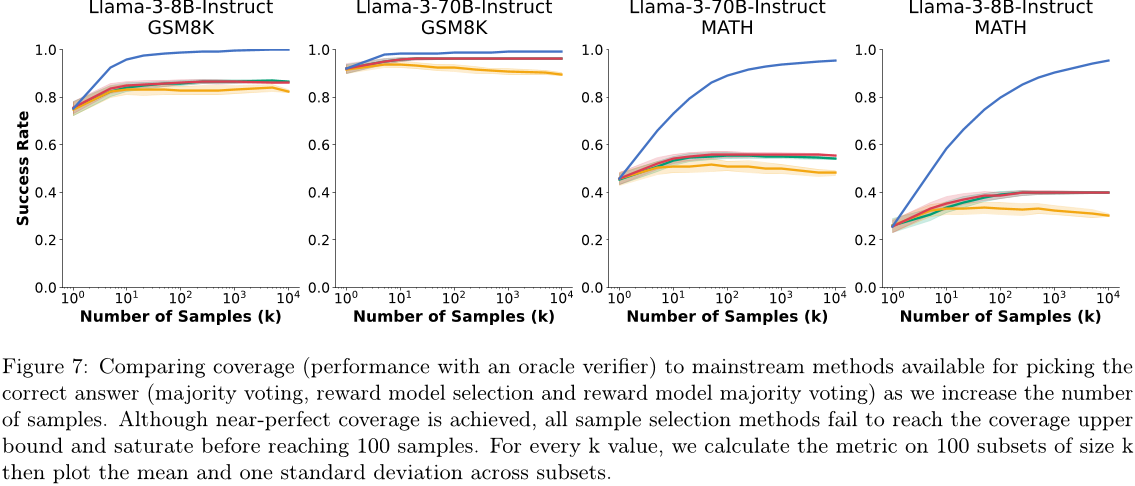
我们使用ArmoRM-Llama3-8B-v0.1作为奖励模型，目前在RewardBench排行榜上，它在开放权重模型中具有最高的推理得分。我们随着样本数量的增加，在图7中报告我们的结果。尽管对于三种方法而言，成功率最初会随着样本数量的增加而提高，但其会在大约100个样本时达到顶峰。同时，覆盖率也会随着样本数量的增加而继续增长，并超过95%。

在多数投票的情况下，这种成功率饱和现象很容易解释。随着样本数量的增加，每个答案所分配的选票比例趋于稳定，因此成功率趋于平缓。对于一些GSM8K和MATH问题，正确解决方案的概率低于百分之一（见图8），它们成为少数样本。随着样本数量的增加，将会有更多的问题出现稀有的正确解决方案，从而提高覆盖率但不提高多数投票的成功率。为了充分受益于重复采样，样本识别方法必须能够解决这些“大海捞针”的情况，并且识别出稀有、正确的样本。

鉴于奖励模型的糟糕表现，我们有理由怀疑验证候选解决方案有多“困难”。在GSM8K和MATH中，仅使用样本的最终答案来评估正确性，中间推理链被排除在外。如果模型在猜测正确的最终答案之前只生成了不合理的推理链，则验证可能不会比从一开始就解决这个问题更容易。通过手动评估Llama-3-8B-Instruct解决方案中的105条推理链，并将其与GSM8K问题进行比较，我们在表2中报告了我们的结果。我们发现，在正确答案很少出现的问题中，超过90％的我们评分的推理链是忠实的。这些正确的推理步骤表明，当识别正确的样本时，验证者可以利用信号。有趣的是，在这个过程中，我们也发现了GSM8K的一个错误的地面真相答案（见附录E）。这个错误的GSM8K问题是Llama-3-70B-Instruct在1万次尝试中没有生成一个“正确”的样本的唯一一个问题。

第 11 页

表2：对Llama-3-8B-Instruct在GSM8K问题上的链式推理的正确性的手动评估。每个问题有三个链式推理被评分。即使对于困难的问题，模型只得到≤10％的样本正确，CoT几乎总是遵循有效的逻辑步骤。有关模型生成和人类标签，请参见此处。

4.2 验证者和软件任务：两个警示故事

软件开发任务可以占据可用验证工具的中间位置。一方面，执行和测试代码的能力允许比使用无结构语言任务更高的自动验证程度。然而，像单元测试这样的工具采用黑盒方法来验证一段代码，并且不如证明检查器等方法全面。这些验证过程中的缺陷可能导致重要的重复采样时出现假阳性或假阴性结果。下面我们提供两个我们在生成第2.1节的结果时遇到的软件验证器缺陷的例子。

4.2.1 SWE-bench Lite中的雪花测试

在生产我们的SWE-bench Lite结果时，我们发现有11.3％的问题具有不一致的测试套件，在运行相同的候选解决方案时不会产生一致的结果。这些不一致的测试偶尔会将数据集的真实问题解决方案分类为错误。此外，某些问题的测试套件取决于候选解决方案而变得非确定性。例如，两个SWE-bench Lite问题涉及操纵Python集合，它们是自然无序的。这些问题的黄金解决方案明确地对集合中的项目进行排序，并且可靠地通过了测试套件。然而，一些模型生成的候选解决方案没有施加这样的排序，因此在某些“幸运”的运行中通过测试而在其他运行中未通过测试。在附录B中，我们列出了所有我们识别出不一致测试的问题ID。我们也报告了从图2中删除有问题的问题的SWE-bench Lite结果，发现与我们在整个数据集上的评估类似的结果。

4.2.2 在CodeContests中的假阴性

CodeContests数据集中的每个问题都附带一组输入输出测试用例，用于评估解决方案的正确性。这些测试用例比早期编码基准（如APPS [23]）更全面，减少了通过所有测试但无法完全解决描述问题的错误解决方案出现的频率。然而，CodeContests测试套件的构建导致了正确的但未能通过测试的虚假负解。

对于某些CodeContests问题，问题描述允许给定测试输入的多个不同正确输出。然而，相应的测试用例并未处理这些场景，而是要求发出特定正确的输出。此外，许多CodeContests测试用例是通过修改原始测试用例来程序生成的。一些被修改的输入违反了问题的输入规格（例如，一个被修改的输入为零而描述承诺的是正整数）。这些错误的测试用例可能导致不同的正确解决方案之间出现不一致的行为。

第 12 页

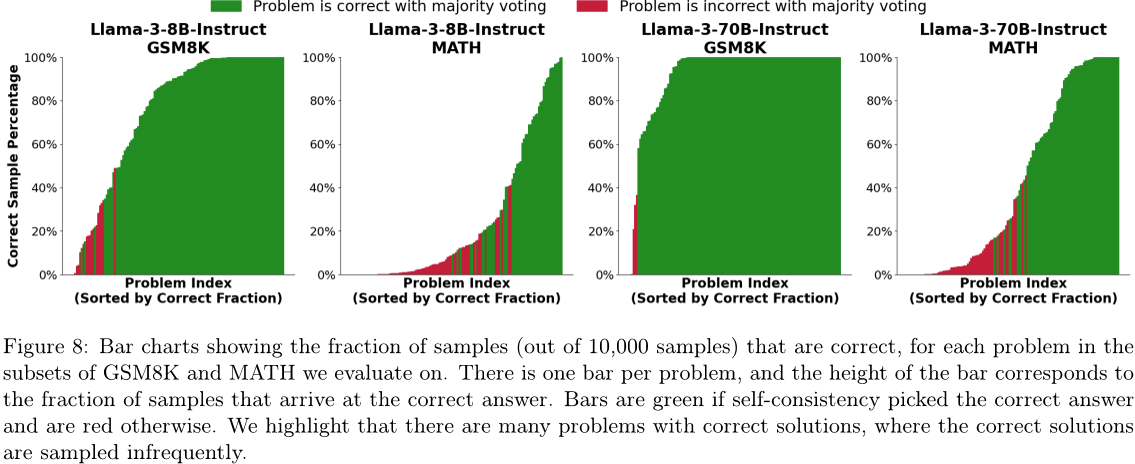
我们通过在CodeContests提供的正确解决方案列表上运行每个问题的测试套件来评估这些问题的普遍性。在包含Python3解决方案的测试集中，有122个问题，我们发现其中35个问题具有“正确的”解决方案，但这些解决方案无法通过相应的测试。由于我们不允许模型查看所有问题的测试用例（及其独特之处），因此对这些问题进行重复采样包含了一种“掷骰子”的元素，以生成不仅正确而且能够通过测试输出特定输出的解决方案。

5 讨论和局限性

在这项工作中，我们探索重复采样作为在推理时间扩展计算的轴心以提高模型性能。在一系列模型和任务中，重复采样可以显着改善使用任何生成样本解决的问题的比例（即覆盖）。当正确解决方案能够被识别时（无论是通过自动验证工具还是其他验证算法），重复采样可以在推理期间放大模型的能力。这种放大可以使较弱模型与许多样本的组合比从更强大、更昂贵的模型中尝试较少次数更加高效和成本效益。

改进重复采样：在我们的实验中，我们探索了重复采样的一个简单版本，在这个版本中，所有对问题的尝试都是使用相同的提示和超参数独立生成的。我们认为这种设置可以进一步优化以提高性能，特别是沿着以下方向进行优化：

解决方案多样性：我们目前依赖正采样温度作为创建样本之间多样性的唯一机制。将此单词级别的采样与其他更高层次的方法相结合，可能能够进一步增加多样性。例如，AlphaCode 使用不同的元数据标签对不同样本进行条件处理。

多轮交互：尽管在解决CodeContests和MiniF2F问题时有自动验证工具可用，但我们仅使用单轮设置，在该设置中模型生成解决方案而没有任何迭代能力。为这些工具提供执行反馈应该会提高解决方案的质量。我们对与这些工具相关的权衡感兴趣。

第 13 页

多轮交互，因为每次尝试都变得更加昂贵，但也可能更有可能成功。

3、从以前的尝试中学习：目前，我们的实验完全隔离了每个尝试。访问现有样本，特别是如果验证工具可以提供反馈时，这可能有助于生成未来的尝试。

重复采样和推断系统：重复采样是一种与服务聊天机器人请求的LLM推理工作负载不同的工作负载。生产聊天机器人的部署强调低响应延迟，遵守延迟目标可能会导致单个设备批次大小降低，并减少硬件利用率。相反，在对单个提示进行多次完成时，可以更注重整体吞吐量并最大化硬件利用率。此外，重复采样可以从利用序列之间提示重叠的专业化注意力优化中受益[32、6、61]。因此，重复采样推理的成本低于直接向聊天机器人API发送许多平行请求的成本。这些成本节省还可以进一步激励选择从便宜的模型中多次采样而不是从昂贵的模型中较少次数地采样。

验证者：我们的第4节结果强调了当无法使用自动工具时，改进样本验证方法的重要性。为模型配备评估其自身输出的能力将允许重复采样扩展到更多任务。特别感兴趣的是将重复采样应用于诸如创造性写作等无结构的任务，这可能需要对不同样本进行更主观的比较，而不是我们考虑的通过/失败任务。开发基于模型的验证器的一个替代方向是设计转换器，可以将一个无结构任务变成可验证的，例如将非正式数学陈述形式化成像Lean这样的语言，以便证明检查器可以应用。

致谢 7

我们感谢Together AI部分赞助了该项目的计算，以及Rahul Chalamala和Ben Athiwaratkun在管理该基础设施方面提供的帮助。我们感谢John Yang在运行我们的SWE-bench实验时给予的建议和支持。最后，我们对Mayee Chen、Neel Guha、Quinn McIntyre、Jon Saad-Falcon和Benjamin Spector在整个项目中提供有益讨论和反馈表示感激之情。

我们衷心感谢NIH在编号为U54EB020405（Mobilize）、NSF在编号CCF2247015（硬件感知）、CCF1763315（稀疏性之外）、CCF1563078（体积到速度）和1937301（RTML）；美国DEVCOM ARL在编号W911NF-23-2-0184（长上下文）和W911NF-21-2-0251（交互式人机团队合作）；ONR在编号N000142312633（深度信号处理）；斯坦福大学HAI在编号247183；NXP、Xilinx、LETI-CEA、Intel、IBM、Microsoft、NEC、Toshiba、TSMC、ARM、Hitachi、BASF、Accenture、Ericsson、Qualcomm、Analog Devices、Google云、Salesforce、Total，以及HAI-GCP云研究计划的赞助商：Meta、Google和VMWare。美国政府有权复制并分发此材料以供政府使用，即使有版权标记也不例外。本材料中表达的所有意见、发现、结论或建议均不代表NIH、ONR或美国政府的观点、政策或认可，无论是明示还是暗示。

这项工作是在克拉伦登奖学金的支持下完成的。

第 15 页

参考文献

[1]Aide.dev，2024。URL：Aide。

[2]你好，gpt-4o，2024。URL：https://openai.com/index/hello-gpt-4o/.

[3]Meta llama 3，2024。URL：https://llama.meta.com/llama3/.

[4] Claude 3.5 sonnet，2024。URL：Introducing Claude 3.5 Sonnet \ Anthropic。

[5] Voyage ai，2024。URL：Voyage.

[6] Ben Athiwaratkun，Sujan Kumar Gonugondla，Sanjay Krishna Gouda，Haifeng Qian，Hantian Ding，Qing Sun，Jun Wang，Jiacheng Guo，Liangfu Chen，Parminder Bhatia，Ramesh Nallapati，Sudipta Sengupta，and Bing Xiang. Bifurcated Attention: Accelerating Massive Parallel Decoding with Shared Prefixes in LLMs, 2024. URL：https://arxiv.org/abs/2403.08845。

[7] 白玉涛，萨鲁瓦·卡达瓦特，桑迪潘·孔杜，阿曼达·阿斯凯尔，杰克逊·肯尼翁，安德鲁·琼斯，安娜·陈，安娜·戈尔迪，阿扎莉亚·米尔霍西尼，卡梅伦·麦克金农，卡罗尔·陈，卡洛琳·奥利森，克里斯托弗·奥拉哈，丹尼·赫南德兹，黛恩·德拉因，深·甘古利，邓斯顿·李，艾力·特兰-约翰逊，埃森·佩雷斯，詹姆斯·柯林斯，贾里德·穆勒，杰夫·拉迪什，乔舒亚·兰道，卡马拉·内多苏，卡米莱·卢科斯维特，丽莲·劳维特，迈克尔·塞利托，纳撒尼尔·埃尔哈格，尼克拉斯·施费尔，诺米·马尔科，诺瓦·达萨玛，罗宾·拉森，萨姆·雷金，斯科特·约翰斯顿，肖娜·克拉韦克，谢尔·埃尔秀克，斯坦尼斯拉夫·福特，塔梅拉·兰汉姆，蒂莫西·泰勒伦-劳顿，汤姆·康瑞利，汤姆·亨尼根，特里斯坦·胡姆，萨姆·R·鲍曼，扎克·哈特菲尔德-多德斯，本·曼，达里奥·阿莫代伊，尼古拉斯·约瑟夫，萨姆·麦坎德利斯，汤姆·布朗和贾里德·卡普兰。宪法人工智能：从人工智能反馈中获得的无害性，2022年。

[8] 马切伊·贝斯塔，尼尔斯·布莱克，阿莱斯·库比切克，罗伯特·格斯特纳格尔，米哈尔·波德扎斯基，卢卡斯·吉安内齐，乔安娜·加尔达，托马什·莱赫曼，胡贝尔特·尼维亚多姆斯基，彼得·尼克齐克和托尔斯滕·霍弗勒。思想图：使用大型语言模型解决复杂问题。人工智能协会年会论文集，第38卷（16）：17682 - 17690，2024 年 3 月。ISSN2159-5399。doi：10.1609/aaai.v38i16.29720。URLGraph of Thoughts: Solving Elaborate Problems with Large Language Models| Proceedings of the AAAI Conference on Artificial Intelligence。

[9]Stella Biderman，Hailey Schoelkopf，Quentin Anthony，Herbie Bradley，Kyle O'Brien，Eric Hallahan，Mohammad Aflah Khan，Shivanshu Purohit，USVSN Sai Prashanth，Edward Raff，Aviya Skowron，Lintang Sutawika和Oskar van der Wal。Pythia：用于分析大型语言模型的套件，2023年。URLhttps://arxiv.org/abs/2304.01373。

[10] Noam Brown，Anton Bakhtin，Adam Lerer和Qucheng Gong。结合深度强化学习与信息不完全游戏的搜索。在第34届国际神经信息处理系统会议论文集上，NIPS'20，红钩，纽约州，美国，2020年。Curran Associates Inc. ISBN 978-1-7138-2954-6。

[11] Tom B. Brown，Benjamin Mann，Nick Ryder，Melanie Subbiah，Jared Kaplan，Prafulla Dhariwal，Arvind Neelakantan，Pranav Shyam，Girish Sastry，Amanda Askell，Sandhini Agarwal，Ariel Herbert-Voss，Gretchen Krueger，Tom Henighan，Rewon Child，Aditya Ramesh，Daniel M. Ziegler，Jeffrey Wu，Clemens Winter，Christopher Hesse，Mark Chen，Eric Sigler，Mateusz Litwin，Scott Gray，Benjamin Chess，Jack Clark，Christopher Berner，Sam McCandlish，Alec Radford，Ilya Sutskever 和 Dario Amodei。语言模型是少量样本学习者，2020年。URL：https://arxiv.org/abs/2005.14165。

第 16 页

[12] 沃尔特·坎贝尔，阿瑟·约瑟夫·霍恩和冯·希丰·胡。深蓝。人工智能，第134卷（1 - 2）：57 - 83，2002年1月。ISSN 0004-3702。DOI：10.1016/S0004-3702（01）00129-1。URL：https://doi.org/10.1016/S0004-3702（01）00129-1。

[13]陈国鑫，廖敏鹏，李成熙和范凯。AlphaMath几乎零：无过程的流程监控，2024年。

[14] Lingjiao Chen，Jared Quincy Davis，Boris Hanin，Peter Bailis，Ion Stoica，Matei Zaharia和James Zou。更多的llm调用是否就是你需要的？朝着复合推理系统的规模定律方向，2024年。URL：https://arxiv.org/abs/2403.02419。

[15] Mark Chen，Jerry Tworek，Heewoo Jun，Qiming Yuan，Henrique Ponde de Oliveira Pinto，Jared Kaplan，Harri Edwards，Yuri Burda，Nicholas Joseph，Greg Brockman，Alex Ray，Raul Puri，Gretchen Krueger，Michael Petrov，Heidy Khlaaf，Girish Sastry，Pamela Mishkin，Brooke Chan，Scott Gray，Nick Ryder，Mikhail Pavlov，Alethea Power，Lukasz Kaiser，Mohammad Bavarian，Clemens Winter，Philippe Tillet，Felipe Petroski Such，Dave Cummings，Matthias Plappert，Fotios Chantzis，Elizabeth Barnes，Ariel Herbert-Voss，William Hebgen Guss，Alex Nichol，Alex Paino，Nikolas Tezak，Jie Tang，Igor Babuschkin，Suchir Balaji，Shantanu Jain，William Saunders，Christopher Hesse，Andrew N. Carr，Jan Leike，Josh Achiam，Vedant Misra，Evan Morikawa，Alec Radford，Matthew Knight，Miles Brundage，Mira Murati，Katie Mayer，Peter Welinder，Bob McGrew，Dario Amodei，Sam McCandlish，Ilya Sutskever，Wojciech Zaremba。基于代码训练的大语言模型评估，2021年。URL：https://arxiv.org/abs/2107.03374。

[16]Fran¸cois Chollet。关于智能的度量，2019年。URL：https://arxiv.org/abs/1911.01547。

[17] Paul Christiano，Jan Leike，Tom B. Brown，Miljan Martic，Shane Legg和Dario Amodei。基于人类偏好的深度强化学习，2017年。URL：https://arxiv.org/abs/1706.03741。

[18]卡尔·科布，维尼特·科萨拉朱，穆罕默德·巴瓦里安，马克·陈，韩秀俊，卢卡斯·凯撒，马蒂亚斯·普拉珀特，杰瑞·图韦克，雅各布·希尔顿，雷伊奇罗·纳卡诺，克里斯托弗·赫塞和约翰·舒尔曼。训练验证者解决数学文字问题，2021年。

[19]DeepSeek-AI等。Deepseek-v2：一种强大的、经济的和高效的混合专家语言模型，2024年。URLhttps://arxiv.org/abs/2405.04434。

[20] Mostafa Dehghani，Anurag Arnab，Lucas Beyer，Ashish Vaswani和Yi Tay。效率的误称，2022年。URL：https://arxiv.org/abs/2110.12894。

[21] 高乐，托马斯·陶，巴伯·阿巴斯，斯塔拉·比德曼，西德·布莱克，安东尼·迪波菲，查尔斯·福斯特，劳伦斯·戈登，杰弗里·许，艾兰·勒诺阿克，李浩楠，凯尔·麦康奈尔，尼古拉斯·穆恩尼霍夫，克里斯·奥齐帕，杰森·方，拉里亚·雷诺兹，海莉·谢洛克福，阿维雅·斯科沃隆，林坦·苏塔威卡，埃里克·唐，安希什·提特，本·王，凯文·王和安迪·周。一种用于少量样本语言模型评估的框架，2023年12月。URL：EleutherAI/lm-evaluation-harness: Major refactor。

[22]Ryan Greenblatt。 Getting 50 Getting 50% (SoTA) on ARC-AGI with GPT-4o — LessWrong， 2024。

第 17 页

[23] Dan Hendrycks，Steven Basart，Saurav Kadavath，Mantas Mazeika，Akul Arora，Ethan Guo，Collin Burns，Samir Puranik，Horace He，Dawn Song，and Jacob Steinhardt。使用应用程序测量编码挑战能力，2021年。

[24]丹·亨德里克斯，科林·伯恩斯，萨鲁瓦·卡达瓦特，阿库尔·阿罗拉，史蒂文·巴斯，埃里克·唐，道恩·宋和雅各布·斯坦哈特。使用数学数据集测量数学问题解决能力，2021年。

[25] Joel Hestness，Sharan Narang，Newsha Ardalani，Gregory Diamos，Heewoo Jun，Hassan Kianinejad，Md。Mostofa Ali Patwary，Yang Yang和Yanqi Zhou。深度学习扩展是可预测的，经验上，2017年。URL：https://arxiv.org/abs/1712.00409。

[26] Jordan Hoffmann，Sebastian Borgeaud，Arthur Mensch，Elena Buchatskaya，Trevor Cai，Eliza Rutherford，Diego de las Casas，Lisa Anne Hendricks，Johannes Welbl，Aidan Clark，Tom Hennigan，Eric Noland，Katie Millican，George van den Driessche，Bogdan Damoc，Aurelia Guy，Simon Osindero，Karen Simonyan，Erich Elsen，Jack W. Rae，Oriol Vinyals，and Laurent Sifre。训练计算最优的大语言模型，2022。URL：https://arxiv.org/abs/2203.15556。

[27] Arian Hosseini，Xingdi Yuan，Nikolay Malkin，Aaron Courville，Alessandro Sordoni和Rishabh Agarwal。V-star：训练自教推理者的验证器，2024年。

[28] Robert Irvine，Douglas Boubert，Vyas Raina，Adian Liusie，Ziyi Zhu，Vineet Mudupalli，Aliaksei Korshuk，Zongyi Liu，Fritz Cremer，Valentin Assassi，Christie-Carol Beauchamp，Xiaoding Lu，Thomas Rialan，and William Beauchamp。奖励聊天机器人与数百万用户的真实世界互动，2023。URL：https://arxiv.org/abs/2303.06135。

[29] 江东福，任翔和林一尘。 Llm-blender：通过对齐和生成融合将大型语言模型进行组合，2023年。URL https://arxiv.org/abs/2306.02561。

[30]Carlos E. Jimenez，John Yang，Alexander Wettig，Shunyu Yao，Kexin Pei，Ofir Press，and Karthik Narasimhan。Swe-bench：Can language models resolve real-world GitHub issues？，2024. URL https://arxiv.org/abs/2310.06770。

[31]Andy L.Jones。用棋盘游戏扩展幂律，2021年。URL：https://arxiv.org/abs/2104.03113。

[32] Jordan Juravsky，Bradley Brown，Ryan Ehrlich，Daniel Y Fu，Christopher R´e和Azalia Mirhoseini。Hydragen：共享前缀的高通量llm推理。arXiv预印本arXiv：2402.05099，2024。

[33] Jared Kaplan，Sam McCandlish，Tom Henighan，Tom B. Brown，Benjamin Chess，Rewon Child，Scott Gray，Alec Radford，Jeffrey Wu和Dario Amodei。神经语言模型的规模定律，2020年。

[34] Sumith Kulal，Panupong Pasupat，Kartik Chandra，Mina Lee，Oded Padon，Alex Aiken，and Percy Liang。Spoc：基于搜索的伪代码到代码，2019年。URL https://arxiv.org/abs/1906.04908。

[35] Nathan Lambert，Valentina Pyatkin，Jacob Morrison，LJ Miranda，Bill Yuchen Lin，Khyathi Chandu，Nouha Dziri，Sachin Kumar，Tom Zick，Yejin Choi，Noah A. Smith，and Hannaneh Hajishirzi。Rewardbench：评估语言建模的奖励模型，2024。URL https://arxiv.org/abs/2403.13787。

第 18 页

[36]Aitor Lewkowycz，Anders Andreassen，David Dohan，Ethan Dyer，Henryk Michalewski，Vinay Ramasesh，Ambrose Slone，Cem Anil，Imanol Schlag，Theo Gutman-Solo，Yuhuai Wu，Behnam Neyshabur，Guy Gur-Ari，and Vedant Misra。使用语言模型解决定量推理问题，2022年。URL：https://arxiv.org/abs/2206.14858。

[37] 李玉佳，乔大卫，中俊英，卡斯曼奈特，施里特维瑟尔，勒布朗德，埃克尔斯，基林，吉梅诺，达拉戈，胡伯特，乔伊，德马森·杜阿托姆，巴布什金，陈新云，黄波森，韦尔布，戈瓦尔，切雷潘诺夫，莫洛伊，丹尼尔·J·曼科沃茨，艾丝美·苏瑟兰·罗宾逊，库霍利，纳多·德弗里斯，卡武丘格卢和奥里奥尔·维尼亚尔斯。与阿尔法代码竞争水平的代码生成。科学，378（6624）：1092-1097，2022年12月。ISSN 1095-9203。doi：10.1126/science.abq1158。URL http://dx.doi.org/10.1126/science.abq1158。

[38] Hunter Lightman，Vineet Kosaraju，Yura Burda，Harri Edwards，Bowen Baker，Teddy Lee，Jan Leike，John Schulman，Ilya Sutskever和Karl Cobbe。让我们一步一步验证，2023年。

[39] Aman Madaan，Niket Tandon，Prakhar Gupta，Skyler Hallinan，Luyu Gao，Sarah Wiegreffe，Uri Alon，Nouha Dziri，Shrimai Prabhumoye，Yiming Yang，Shashank Gupta，Bodhisattwa Prasad Majumder，Katherine Hermann，Sean Welleck，Amir Yazdanbakhsh，and Peter Clark。Self-refine：Iterative refinement with self-feedback，2023. URL https://arxiv.org/abs/2303.17651。

[40] Isaac Ong，Amjad Almahairi，Vincent Wu，Wei-Lin Chiang，Tianhao Wu，Joseph E. Gonzalez，M Waleed Kadous，and Ion Stoica。Routellm：学习使用偏好数据路由llms，2024。URL https://arxiv.org/abs/2406.18665。

[41]OpenAI等。GPT-4技术报告，2024年。URL：https://arxiv.org/abs/2303.08774。

[42] Alec Radford，Jeff Wu，Rewon Child，David Luan，Dario Amodei和Ilya Sutskever。语言模型是无监督的多任务学习者。2019年。

[43] Baptiste Rozi`ere，Jonas Gehring，Fabian Gloeckle，Sten Sootla，Itai Gat，Xiaoqing Ellen Tan，Yossi Adi，Jingyu Liu，Romain Sauvestre，Tal Remez，J´er´emy Rapin，Artyom Kozhevnikov，Ivan Evtimov，Joanna Bitton，Manish Bhatt，Cristian Canton Ferrer，Aaron Grattafiori，Wenhan Xiong，Alexandre D´efossez，Jade Copet，Faisal Azhar，Hugo Touvron，Louis Martin，Nicolas Usunier，Thomas Scialom，and Gabriel Synnaeve. Code llama：Open foundation models for code，2023. URL https://arxiv.org/abs/2308.12950。

[44]刘林邵，杰奎琳·赫，阿卡里·阿萨伊，魏佳石，蒂姆·德特默斯，赛文·闵，卢克·泽特勒莫耶尔和潘·韦·科。使用万亿个标记的数据存储扩展基于检索的语言模型，2024年。URL：https://arxiv.org/abs/2407.12854

[45]大卫·西尔弗，托马斯·胡伯特，朱利安·施里特维瑟，伊奥尼奥斯·安东戈洛，马修·赖，阿图尔·古兹，马克·兰克托，劳伦特·西弗雷，达拉斯·库马拉恩，托尔·格拉佩尔，蒂莫西·莉莉克拉普，卡伦·西蒙扬和德米斯·哈萨比斯。通过自我游戏掌握国际象棋和将棋的通用强化学习算法，2017年。

[46] 松一帆，王国印，李树健和林宇晨。好、坏与贪婪：不应忽视非确定性，对llm的评估，2024年。URL https://arxiv.org/abs/2407.10457。

[47]Gemini团队等。Gemini：一个高度多模态的模型家族，2024年。URLhttps://arxiv.org/abs/2312.11805。

第 19 页

[48] Gemma Team et al. Gemma: Open models based on gemini research and technology, 2024. URL https://arxiv.org/abs/2403.08295。

[49]叶天，彭宝林，宋林峰，金立峰，于典，米海涛和于东。通过想象、搜索和批评来提高llm的自我改进能力，2024年。URL：https://arxiv.org/abs/2404.12253。

[50] 杜辉，吴玉海，黎国伟，何和，黄长。无需人类演示的奥林匹克几何学问题求解。自然杂志，625（7995）：476-482，2024。ISSN 1476-4687。doi：10.1038/s41586-023-06747-5。URL Solving olympiad geometry without human demonstrations | Nature。

[51] Pauli Virtanen，Ralf Gommers，Travis E. Oliphant，Matt Haberland，Tyler Reddy，David Cournapeau，Evgeni Burovski，Pearu Peterson，Warren Weckesser，Jonathan Bright，St´efan J. van der Walt，Matthew Brett，Joshua Wilson，K. Jarrod Millman，Nikolay Mayorov，Andrew R. J. Nelson，Eric Jones，Robert Kern，Eric Larson，C J Carey，I˙lhan Polat，Yu Feng，Eric W. Moore，Jake VanderPlas，Denis Laxalde，Josef Perktold，Robert Cimrman，Ian Henriksen，E. A. Quintero，Charles R. Harris，Anne M. Archibald，Antoˆnio H. Ribeiro，Fabian Pedregosa，Paul van Mulbregt，and SciPy 1.0 Contributors. SciPy 1.0：Fundamental Algorithms for Scientific Computing in Python. Nature Methods, 17:261–272, 2020. doi: 10.1038/s41592-019-0686-2。

[52] Fanqi Wan，Xinting Huang，Deng Cai，Xiaojun Quan，Wei Bi，and Shuming Shi. 大语言模型的知识融合，2024。URL：https://arxiv.org/abs/2401.10491。

[53] Wang Haoxiang，Xiong Wei，Xie Tengyang，Zhao Han，and Zhang Tong. 可解释的偏好通过多目标奖励建模和专家混合物，2024。URL：https://arxiv.org/abs/2406.12845。

[54] Wang Junlin，Wang Jue，Athiwaratkun Ben，Zhang Ce，and Zou James. A mixture of agents enhances large language model capabilities, 2024. URL https://arxiv.org/abs/2406.04692。

[55]王学志，魏嘉，舒尔曼斯·戴尔，黎奎克，奇·埃德，纳朗·沙兰，乔坎什·乔杜里和周登尼。自我一致性改善了语言模型的链式推理，2023年。

[56] 芮思杰，王雪志，舒尔曼斯，博斯马，伊克特，夏飞，奇，黎，周。链式思维提示在大型语言模型中引发推理，2023年。

[57] 邢宇尧，赵杰夫，于典，杜楠，沙弗兰伊扎克，纳拉西曼卡里希克，曹元。React：语言模型中的推理和行动协同，2022年。URL https://arxiv.org/abs/2210.03629。

[58] Yao Shunyu，Yu Dian，Zhao Jiefei，Shafran Izhak，Griffiths Thomas L., Cao Yuan, and Narasimhan Karthik. Thoughts tree：deliberate problem solving with large language models, 2023. URL https://arxiv.org/abs/2305.10601。

[59]Eric Zelikman，Georges Harik，Yijia Shao，Varuna Jayasiri，Nick Haber和Noah D. Goodman。Quiet-star：语言模型可以教自己在说话之前思考，2024年。URLhttps://arxiv.org/abs/2403.09629。

[60] 郑坤昊，汉杰西尔迈克尔和斯坦尼斯拉斯波卢。Minif2f：一种正式奥林匹克数学水平的跨系统基准测试。arXiv预印本arXiv：2109.00110，2021年。

第 20 页

[61] 郑连民，殷良生，谢志强，孙楚月，黄杰夫，于浩，曹世义，科斯托·科齐拉基斯，伊翁·斯托卡，乔瑟夫·E·戈麦兹，克拉克·巴雷特和应胜。Sglang：结构化语言模型程序的高效执行，2024年。URL https://arxiv.org/abs/2312.07104。

[62]阿尔伯特·奥尔瓦尔。无护城河工具。GitHub - aorwall/moatless-tools at a1017b78e3e69e7d205b1a3faa83a7d19fce3fa6，2024。

第 21 页

采样实验设置

A.1 瘦身正式证明

我们报告了在lean4 MiniF2F数据集的测试集中与形式化MATH问题相对应的130个问题的结果。该数据集是从郑等人的固定版本[60]中创建的原始MiniF2F数据集衍生而来。我们以温度为0.5进行采样，并且不使用核采样。对于每个问题，我们生成10,000个样本。我们从验证集中的以下5个定理的证明作为少样本示例：

• mathd_algebra_116

• amc12_2000_p5

• mathd_algebra_132

• 数学代数 11 <

• mathd_numbertheory_84

我们的提示包括：

几个例子。

在HuggingFace数据集cat-searcher/minif2f-lean4dataset中的每个问题中，都存在头文件导入。这是上传的lean4 MiniF2F数据集。

定理定义。为了防止从定理名称中泄露如何解决该定理的信息，我们用theorem_i替换定理的名称。i∈{1, 2, 3, 4, 5}用于少量示例，i = 6用于当前问题。

我们为生成的解决方案设置了最大令牌长度为200。为了对解决方案进行评分，我们使用了lean-dojo 1.1.2库和lean版本4.3.0-rc2。对于每个战术步骤，我们都设置了一个10秒的超时时间。

第 23 页

A.2 竞赛代码

我们报告了不包括问题描述中的图像标签的测试集上的140个问题的结果。我们以温度为0.6和top-p值为0.95进行采样，这与CodeLlama [43] 的实验一致。对于每个问题，我们生成10,000个样本。我们从训练集中随机选择两个少样本示例作为每个问题的两组少样本示例。我们将生成解决方案的最大令牌长度设置为1024。我们使用与[37]相同的答案比较函数，并使用公共、私人和生成的测试的合并来验证解决方案的正确性。

第 24 页

A.3 数学

我们报告了在随机选择的测试集问题上的结果。我们以温度为0.6进行采样，并且不使用核采样。对于每个问题，我们使用来自[36]中的固定5个少样本示例。

第 25 页

我们为每个问题生成了10，000个样本。我们将生成的解决方案的最大令牌长度设置为512。为了对解决方案进行评分，我们使用LMEval [21]中的minerva_math函数。

少样本示例

示例提示

问题：

函数的域是什么

以区间或区间并集的形式表达你的答案。

解决方案：

A.4 GSM8K

我们报告了对128个随机采样的测试集问题的结果。我们以温度为0.6进行采样，并且不使用核心采样。我们从训练集中随机抽取每个问题的五个少样本示例，作为生成解决方案的输入。我们每题生成10,000个样本。我们将生成解决方案的最大令牌长度设置为512。为了评估解决方案，我们遵循LMEval [21] 。

少样本示例

问题：詹姆斯决定换车。他以八折的价格卖掉了他的2万美元的汽车，然后能够讨价还价买一辆标价为3万美元的新车，价格是九折。他总共花了多少钱？答案：他以200000.8=16000美元的价格卖掉了自己的汽车；他以300000.9=27000美元的价格买了一辆新车。这意味着他总共花费了11000美元。#### 11000

示例提示

问题：玛丽的储藏室里有6罐糖霜。每罐糖霜可以装饰8个纸杯蛋糕。玛丽想烤足够的纸杯蛋糕，用完所有的糖霜。如果每个托盘能装12个纸杯蛋糕，她应该烤多少个托盘的纸杯蛋糕？答案：

第 26 页

B SWE-bench Lite

B.1 实验设置

对于我们的实验，我们使用DeepSeek-V2-Coder-Instruct模型和Moatless Tools代理框架（在提交a1017b78e3e69e7d205b1a3faa83a7d19fce3fa6时）。我们使用Voyage AI [5]嵌入进行检索，这是默认由Moatless Tools使用的。我们没有对模型或框架进行任何修改，完全将其作为现成的组件来使用。

使用此设置，我们对每个问题进行标准温度采样，并独立完成250次。为了确定最佳采样温度，我们在测试集的随机子集中（共50个问题）进行了温度扫描，测试了温度为1.0、1.4、1.6和1.8的情况。根据这些结果，我们选择了1.6作为主要实验中的温度。

B.2 测试套件的不稳定性

在我们的分析中，我们识别了SWE-bench Lite中的34个问题，这些测试套件包含有易变的测试。使用SWE-bench的作者提供的测试框架，我们对每个解决方案进行了多次测试：对于某些解决方案，有时该解决方案被标记为正确，而其他时候则被标记为错误。在这34个实例中有30个，在正确的解决方案上也观察到了易变性。表3列出了具有易变测试的34个实例的问题ID。

另外，astropy astropy-6938在某些机器上是不稳定的，在其他机器上则不是。SWE-bench的作者能够重现这种不稳定；然而我们无法做到这一点。我们的初步调查表明这个问题是由docker环境中运行单元测试的依赖项的未锁定版本引起的。

在这里，我们包括了表3中删除问题的子集的结果（共266个问题）。对于全数据集评估，在任何具有易变测试的问题上，我们运行测试套件11次，并使用多数投票来确定解决方案是否通过或失败。对于没有易变测试的子集的评估，我们比较的所有基准都正确地解决了哪些问题，因此我们简单地删除了带有易变测试的问题并重新计算其分数。

第 27 页

A CodeStory Aide + Mixed Models Single-Attempt (SOTA) Moatless Tools + GPT-4o Single-Attempt

C 规模定律详情

C.1 实验细节

为了拟合指数幂律，我们首先在从0到10,000的对数尺度上均匀地采样40个点，并删除重复项。然后，我们使用SciPy的[51]曲线拟合函数来找到方程3中最佳拟合这些点的a和b参数。

C.2 增加结果

在图10中，我们展示了对扩展数据集和模型的覆盖曲线进行幂律拟合的结果。

第 28 页

覆盖范围：幂律拟合，c = exp（ak - b）

样本数量（k）样本数量（k）

第 29 页

D 精确细节

为了计算多数投票，我们使用了Reward模型+最佳N个和Reward模型+多数投票指标。我们在第2节中介绍的MATH和GSM8K数据集上使用相同的128个问题子集进行计算。每个问题对应于我们测试的每个模型的10,000个样本。对于每种验证方法，我们取k大小为100的随机子集，并使用每个子集计算成功率。我们在图7中报告子集之间的平均值和标准差。为了计算多数投票答案，我们从每个子集中获取多数答案。对于Reward模型+最佳N个，我们选择由奖励模型分配最高分数的答案。对于Reward模型+多数投票指标，我们对所有具有相同最终答案的所有样本的奖励模型得分求和，并使用具有最高总分的最终答案。

第 30 页