
DeepSeek薪资待遇曝光!确实很香。。。
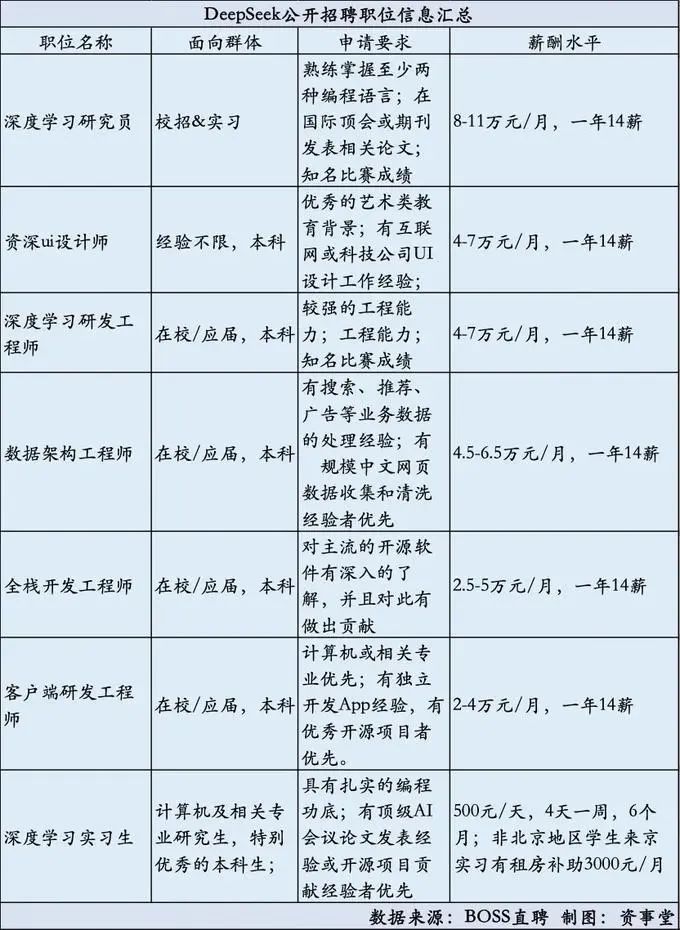
但最牛的是他们的招聘标准——不要繁琐技能清单,不问几年经验,只看三点:能力、对开源的热爱、自驱力。最近DeepSeek这家公司真的火出了圈,搞了个100%开源的大模型R1,不仅性能能和OpenAI的o1对标,训练成本还不到ChatGPT的5%。普通岗位25K起步,顶级能拿到80K甚至110K,年薪14薪,实习生也能日薪500+,外地实习生还有房补。毕竟,现在不少大厂都在裁员,DeepSeek不仅给
最近DeepSeek这家公司真的火出了圈,搞了个100%开源的大模型R1,不仅性能能和OpenAI的o1对标,训练成本还不到ChatGPT的5%。你没听错,别人烧微软100亿美金。硅谷那些大佬估计晚上睡觉都不安稳了。

这家公司规模不大,才140人左右,但薪资待遇一点也不寒酸。普通岗位25K起步,顶级能拿到80K甚至110K,年薪14薪,实习生也能日薪500+,外地实习生还有房补。这待遇,在如今的大环境下,确实有点狠。
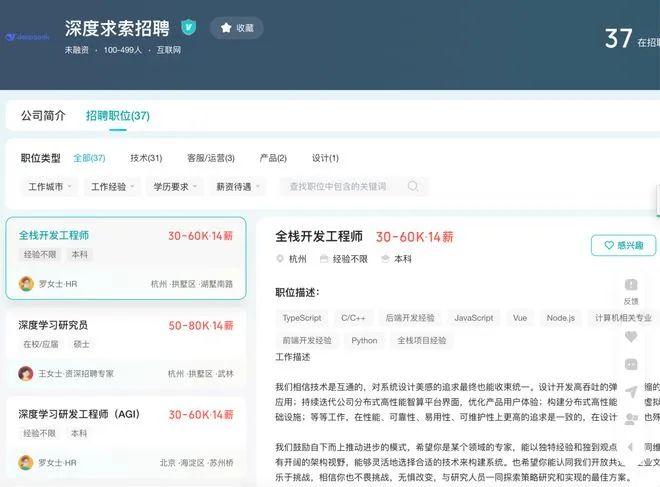
但最牛的是他们的招聘标准——不要繁琐技能清单,不问几年经验,只看三点:能力、对开源的热爱、自驱力。别的公司筛简历全是“3-5年经验起步”,DeepSeek直接告诉你:“不一定要做过才能做。”这对很多年轻人来说简直是天降福音。
说真的,这种公司少见但太香了。毕竟,现在不少大厂都在裁员,DeepSeek不仅给高薪,还愿意给新人机会。要是有兴趣搞AI,又喜欢开源,真的可以冲一波,毕竟这种机会可不是天天有的【备注:文末可领最新资料】。
今日算法题
好了,我们回归正题,今天咱们聊个挺有趣的问题——给一堆数字加上+或-,看看能不能凑出一个目标值。这个问题看起来像是在玩数学游戏,但其实是个标准的动态规划问题,当然,也可以用回溯暴力解决。
不过要是真这么干,可能会被面试官劝退。咱们一步步拆解一下,看怎么优雅地拿下这个问题。
首先,这题的意思很简单,给你一个数组nums和一个目标值target,你可以在每个数前面加上+或-,然后算出最终的值,问你有多少种不同的方式能让最终结果等于target。
比如说,nums = [1, 1, 1, 1, 1],target = 3,那么符合条件的表达式有:
+1 +1 +1 +1 -1 = 3
+1 +1 +1 -1 +1 = 3
+1 +1 -1 +1 +1 = 3
+1 -1 +1 +1 +1 = 3
-1 +1 +1 +1 +1 = 3
总共有5种不同的方式。
如果暴力穷举,我们可以直接用回溯,每个数都有两种选择,加+或者加-,一共2^n种可能,遍历所有情况,看哪种能得到目标值。这种方法简单粗暴,代码也很好写,但问题是,n大了以后就会超时,比如n=20还勉强可以接受,但n=40直接GG。
def findTargetSumWays(nums, target):
def backtrack(index, current_sum):
if index == len(nums):
return 1 if current_sum == target else 0
return backtrack(index + 1, current_sum + nums[index]) + backtrack(index + 1, current_sum - nums[index])
return backtrack(0, 0)
这个方法虽然直观,但时间复杂度是O(2^n),遇到大数组就跑不动了。
为了优化,我们可以用动态规划。核心思想是把问题转换成子集和问题,也就是在nums里找出一个子集,使得它的和等于(sum(nums) + target) / 2,如果这个数是个负数或者是个奇数,说明直接没解。
具体来说,我们用一个dp数组,dp[j]表示能凑成和为j的方法数,然后遍历nums,每个数可以选择或者不选择,最终我们就能得到有多少种方法能凑成这个目标。
def findTargetSumWays(nums, target):
total = sum(nums)
if (total + target) % 2 == 1 or total < abs(target):
return 0
subset_sum = (total + target) // 2
dp = [0] * (subset_sum + 1)
dp[0] = 1 # 凑成0的方法数是1(什么都不选)
for num in nums:
for j in range(subset_sum, num - 1, -1):
dp[j] += dp[j - num]
return dp[subset_sum]
这个方法的时间复杂度是O(n * sum(nums)),远远优于O(2^n)的暴力解,面试官看到后应该不会直接劝退。
总结一下,这道题的核心是:如果直接暴力枚举,会超时,所以我们用转换成子集和问题的方法,动态规划搞定。这样一来,不管是n=20还是n=1000,代码都能轻松跑完。
更多推荐
 已为社区贡献10条内容
已为社区贡献10条内容









所有评论(0)