神经网络的向量化表示

我们已经知道深层的神经网络的结构大概是下面的样子，但是这张图背后到底是怎样的，这个 x 和 y 还有参数到底长什么样子呢？

这就要提到神经网络的向量化表示

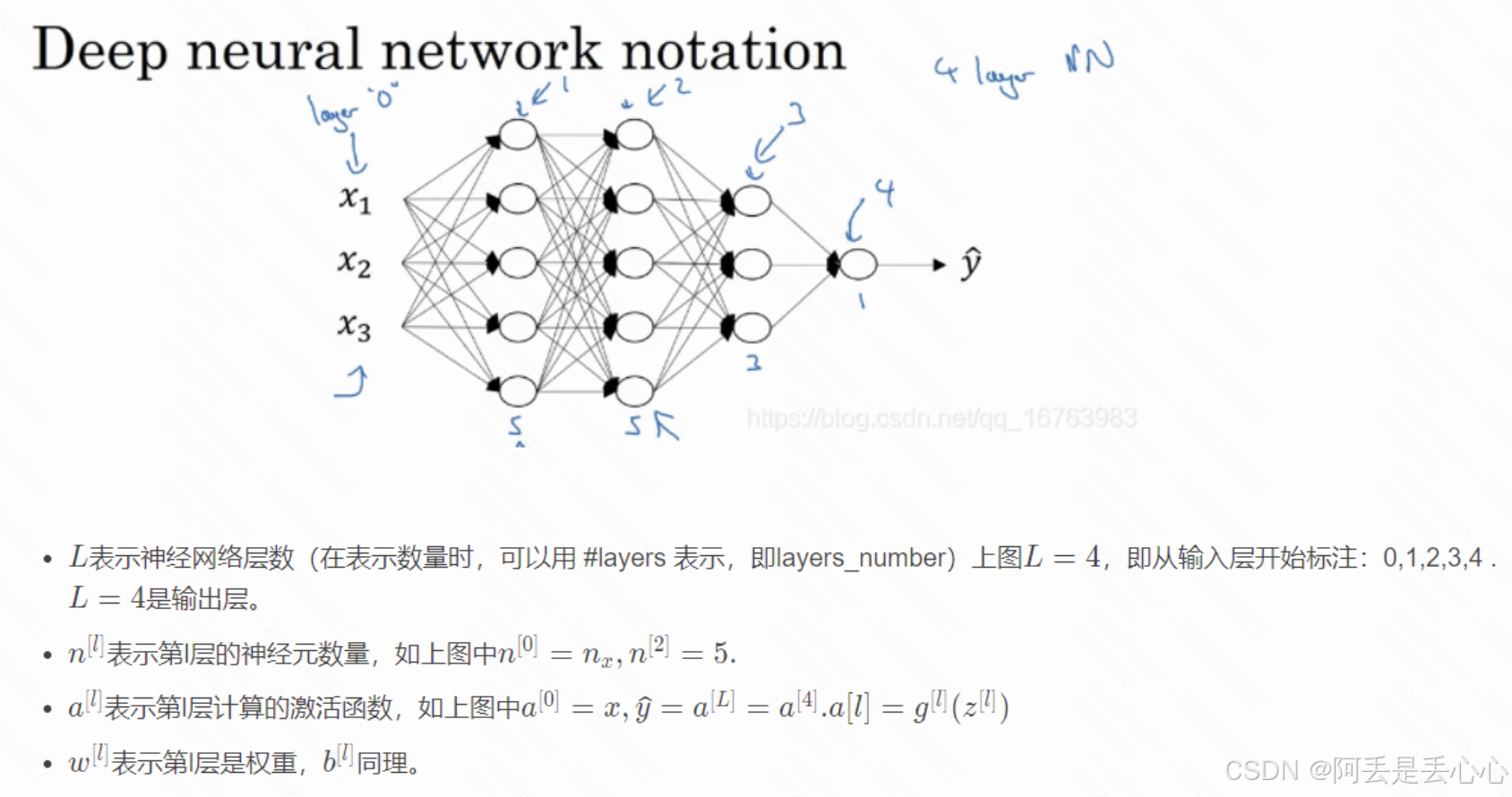
针对上面这个 4 层神经网络，它的代码如下

class NeuralNetwork(nn.Module):
    def __init__(self):
        super(NeuralNetwork, self).__init__()
        # 网络结构：输入层(3) -> 隐藏层1(2) -> 隐藏层2(3) -> 隐藏层3(3) -> 输出层(1)
        self.layer1 = nn.Linear(3, 5)  # 输入层到第一隐藏层
        self.layer2 = nn.Linear(5, 5)  # 第一隐藏层到第二隐藏层
        self.layer3 = nn.Linear(5, 3)  # 第二隐藏层到第三隐藏层
        self.layer4 = nn.Linear(3, 1)  # 第三隐藏层到输出层
        
        self.activation = nn.ReLU()  # 激活函数
        
    def forward(self, x):
        # 前向传播
        x = self.activation(self.layer1(x))
        x = self.activation(self.layer2(x))
        x = self.activation(self.layer3(x))
        x = self.layer4(x)  # 输出层通常不使用激活函数
        return x

现在我们模拟一些输入数据

# 模拟一些训练数据
def generate_data(n_samples=1000):
    X = np.random.randn(n_samples, 3)  # 随机生成输入特征
    # 创建一个非线性关系作为目标
    y = X[:, 0]**2 + 2*X[:, 1] - 0.5*X[:, 2] + np.random.randn(n_samples)*0.1
    y = y.reshape(-1, 1)
    return torch.FloatTensor(X), torch.FloatTensor(y)

# 生成训练和测试数据
X_train, y_train = generate_data(800)
X_test, y_test = generate_data(200)

print(X_train.shape)
print(y_train.shape)
X_train, y_train

从输出可以看出 X 是一个 800*3 的向量，y 是一个 800*1 的向量

接下来我们再看一下初始化后这个神经网络的初始参数


# 查看权重形状和数值
print("Weight shape:", model.layer1.weight.shape)  # 输出：torch.Size([4, 8])
print("Weight values:\n", model.layer1.weight.data)

print("Bias shape:", model.layer2.bias.shape)     # 输出：torch.Size([4])
print("Bias values:\n", model.layer2.bias.data)

我这边初始化的结果如下 

Weight shape: torch.Size([5, 3])
Weight values:
 tensor([[-9.3005e-01, -3.9959e-04,  1.1454e-02],
        [-1.1399e-01, -5.3568e-01,  1.1318e-01],
        [ 8.0823e-01,  1.4906e-01, -5.2917e-02],
        [-9.6269e-01,  5.3325e-01, -1.5497e-01],
        [ 1.2920e+00,  1.0793e-02, -1.2165e-02]])
Bias shape: torch.Size([5])
Bias values:
 tensor([-1.1184,  1.4452, -1.2177,  1.3206, -0.0058])

这里面Weight shape就相当于上篇文章（【从0到1搞懂大模型】一切都从线性回归开始讲起（1）-CSDN博客）提到的 w，Bias就相当于上篇文章提到的 b，而正是这些参数构成了我们的神经网络，而后续对于模型进行训练调优也就是对这个参数进行不断更新的过程，使得这个模型愈来愈趋近于真实世界。

梯度下降

关于梯度下降&反向传播已经有很多博主写过相关帖子了，我这边推荐几个

https://www.zhihu.com/question/305638940

https://www.youtube.com/watch?v=s7BxboxEfnU

训练神经网络的三步骤

  • 正向计算网络输出
  • 计算loss
  • 反向传播，计算loss的梯度来更新参数

之前已经说到，神经网络训练的过程其实就是想让 loss逐步变小，或者说让预测的 y 值跟实际的 y 值逐渐逼近，而这整个过程其实就是通过对参数求偏导，让原参数减去这个偏导值逐步更新参数实现的。

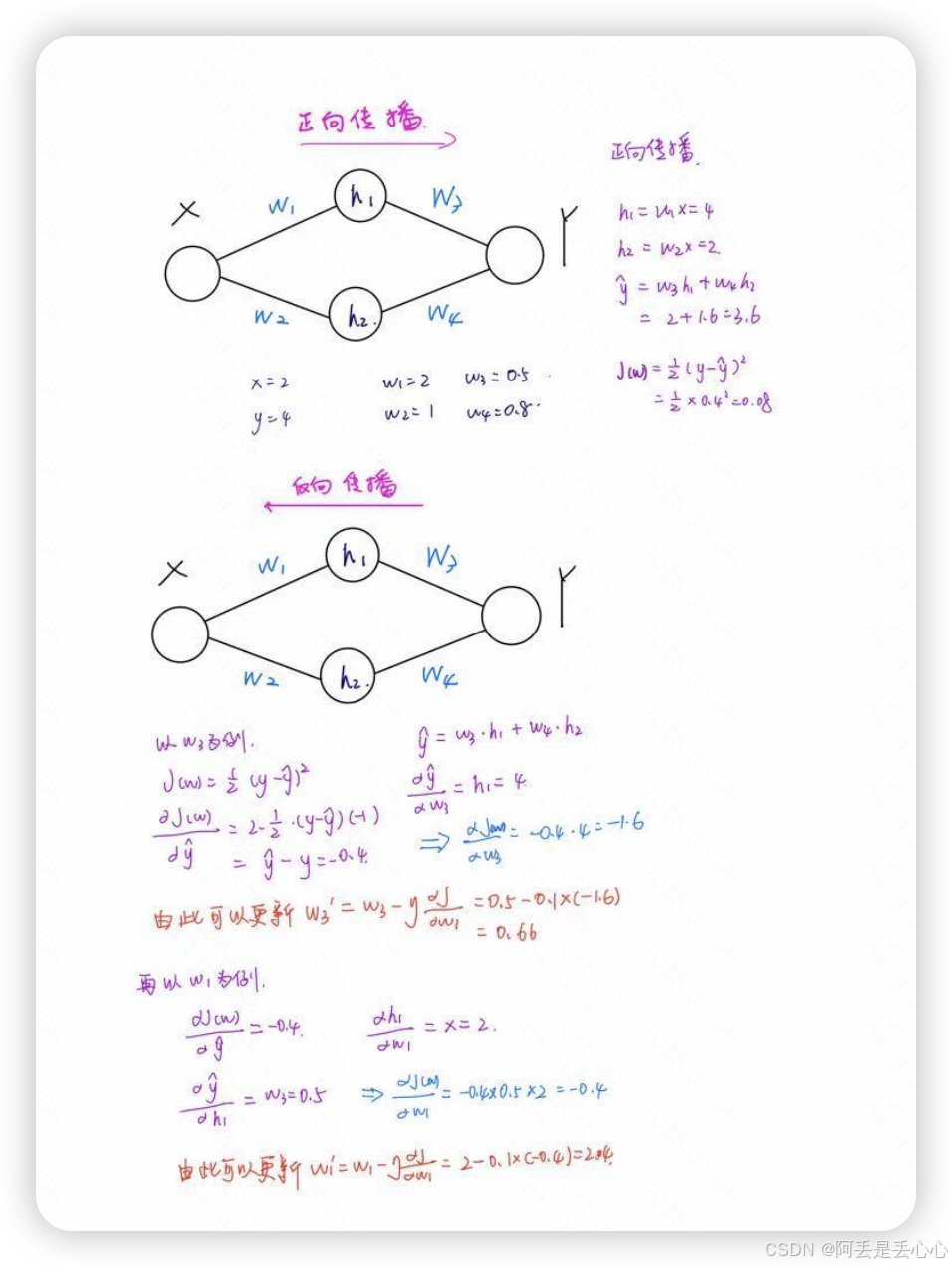
现在我用一个简单的例子展示一下每次训练各个参数是如何变化的

import torch
import torch.nn as nn
import torch.optim as optim

# 定义一个简单的神经网络
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.layer1 = nn.Linear(1, 2)  # 输入层到隐藏层（1 -> 2）
        self.layer2 = nn.Linear(2, 1)  # 隐藏层到输出层（2 -> 1）
        self.activation = nn.ReLU()  # 激活函数

    def forward(self, x):
        x = self.activation(self.layer1(x))  # 隐藏层前向传播
        x = self.layer2(x)  # 输出层前向传播
        return x

# 创建模型实例
model = SimpleNN()

# 创建一个简单的输入数据
X = torch.tensor([[2.0]])  # 输入特征，大小为1
y_true = torch.tensor([[4.0]])  # 真实标签

# 定义损失函数和优化器
criterion = nn.MSELoss()  # 均方误差损失
optimizer = optim.SGD(model.parameters(), lr=0.01)  # 随机梯度下降优化器

# 训练步骤（1步）
print("Initial parameters:")
for name, param in model.named_parameters():
    print(f"{name} - {param.data}")

# 前向传播
output = model(X)
print("\nOutput after forward pass:", output)

# 计算损失
loss = criterion(output, y_true)
print("\nLoss:", loss.item())

# 反向传播
optimizer.zero_grad()  # 清除之前的梯度
loss.backward()  # 计算梯度
print("\nGradients after backward pass:")
for name, param in model.named_parameters():
    print(f"{name} - Gradient: {param.grad}")

# 更新参数
optimizer.step()  # 更新参数

print("\nUpdated parameters:")
for name, param in model.named_parameters():
    print(f"{name} - {param.data}")

# 前向传播
output = model(X)
print("\nOutput after forward pass:", output)

# 计算损失
loss = criterion(output, y_true)
print("\nLoss:", loss.item())

下面是我电脑上得到的结果 

Initial parameters:
layer1.weight - tensor([[ 0.6319],
        [-0.2972]])
layer1.bias - tensor([-0.3607,  0.7175])
layer2.weight - tensor([[-0.3385, -0.0031]])
layer2.bias - tensor([-0.3377])

Output after forward pass: tensor([[-0.6438]], grad_fn=<AddmmBackward0>)

Loss: 21.564632415771484

Gradients after backward pass:
layer1.weight - Gradient: tensor([[6.2878],
        [0.0582]])
layer1.bias - Gradient: tensor([3.1439, 0.0291])
layer2.weight - Gradient: tensor([[-8.3868, -1.1434]])
layer2.bias - Gradient: tensor([-9.2875])

Updated parameters:
layer1.weight - tensor([[ 0.5690],
        [-0.2978]])
layer1.bias - tensor([-0.3921,  0.7172])
layer2.weight - tensor([[-0.2546,  0.0083]])
layer2.bias - tensor([-0.2448])

Output after forward pass: tensor([[-0.4337]], grad_fn=<AddmmBackward0>)

Loss: 19.658052444458008

 

如果将这个更形象的用图的方式展示大概就是(快速手绘的，不美观且口算可能错误，请见谅）

但整体就是一个链式求导更新参数的过程

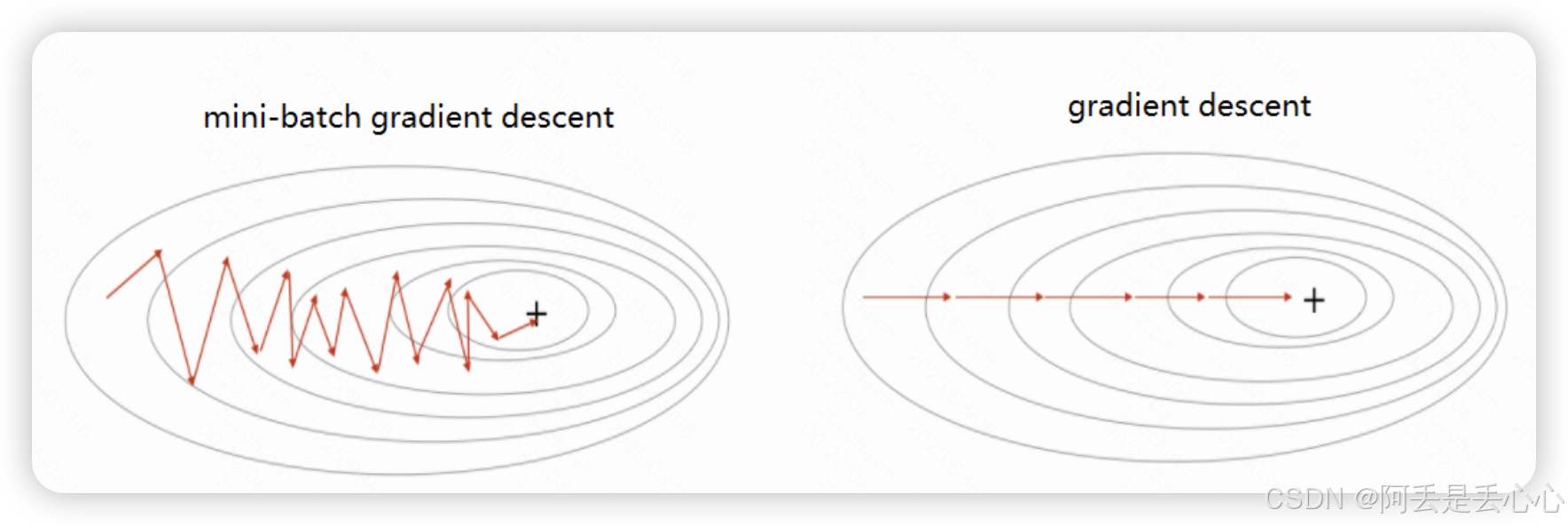
各种梯度下降方法

在小的训练集上联系的时候，通常每次对所有样本计算Loss之后通过梯度下降的方式更新参数(批量梯度下降)，但是在大的训练集时，这样每次计算所有样本的Loss再计算一次梯度更新参数的方式效率是很低的。因此就有了随机梯度下降和mini-batch梯度下降的方式。下面来具体讲讲。

(1)批量梯度下降（batch gradient descent）

 每个epoch计算所有样本的loss，进而计算梯度进行反向传播

for i in range(nb_epochs):
    params_grad = evaluate_gradient(loss_function, data, params)
    params = params - learning_rate * params_grad

其中，m 为训练集样本数，l 为损失函数，ϵ 表示学习率。批量梯度下降的优缺点如下：

  • 优点

每个epoch通过所有样本来计算Loss，这样计算出的Loss更能表示当前分类器在于整个训练集的表现，得到的梯度的方向也更能代表全局极小值点的方向。如果损失函数为凸函数，那么这种方式一定可以找到全局最优解。

  • 缺点

每次都需要用所有样本来计算Loss，在样本数量非常大的时候即使也只能有限的并行计算，并且在每个epoch计算所有样本Loss后只更新一次参数，即只进行一次梯度下降操作，效率非常低。

(2)随机梯度下降（stochastic gradient descent）

 for i in range(nb_epochs):
    np.random.shuffle(data)
    for example in data:
        params_grad = evaluate_gradient(loss_function, example, params)
        params = params - learning_rate * params_grad

随机梯度下降每次迭代(iteration)计算单个样本的损失并进行梯度下降更新参数，这样在每轮epoch就能进行 m 次参数更新。看优缺点吧：

  • 优点

参数更新速度大大加快，因为计算完每个样本的Loss都会进行一次参数更新

  • 缺点

1.计算量大且无法并行。批量梯度下降能够利用矩阵运算和并行计算来计算Loss，但是SGD每遍历到一个样本就进行梯度计算和参数下降，无法进行有效的并行计算。

2.容易陷入局部最优导致模型准确率下降。因为单个样本的Loss无法代替全局Loss，这样计算出来的梯度方向也会和全局最优的方向存在偏离。但是由于样本数量多，总体的Loss会保持降低，只不过Loss的变化曲线会存在较大的波动。

 (3)小批量梯度下降（mini-batch gradient descent）

for i in range(nb_epochs):
    np.random.shuffle(data):
        for batch in get_batches(data, batch_size=50):
            params_grad = evaluate_gradient(loss_function, batch, params)
            params = params - learning_rate*params_grd

小批量梯度下降将所有的训练样本划分到 batches 个min-batch中，每个mini-batch包含 batchsize 个训练样本。每个iteration计算一个mini-batch中的样本的Loss，进而进梯度下降和参数更新，这样兼顾了批量梯度下降的准确度和随机梯度下降的更新效率。 

 

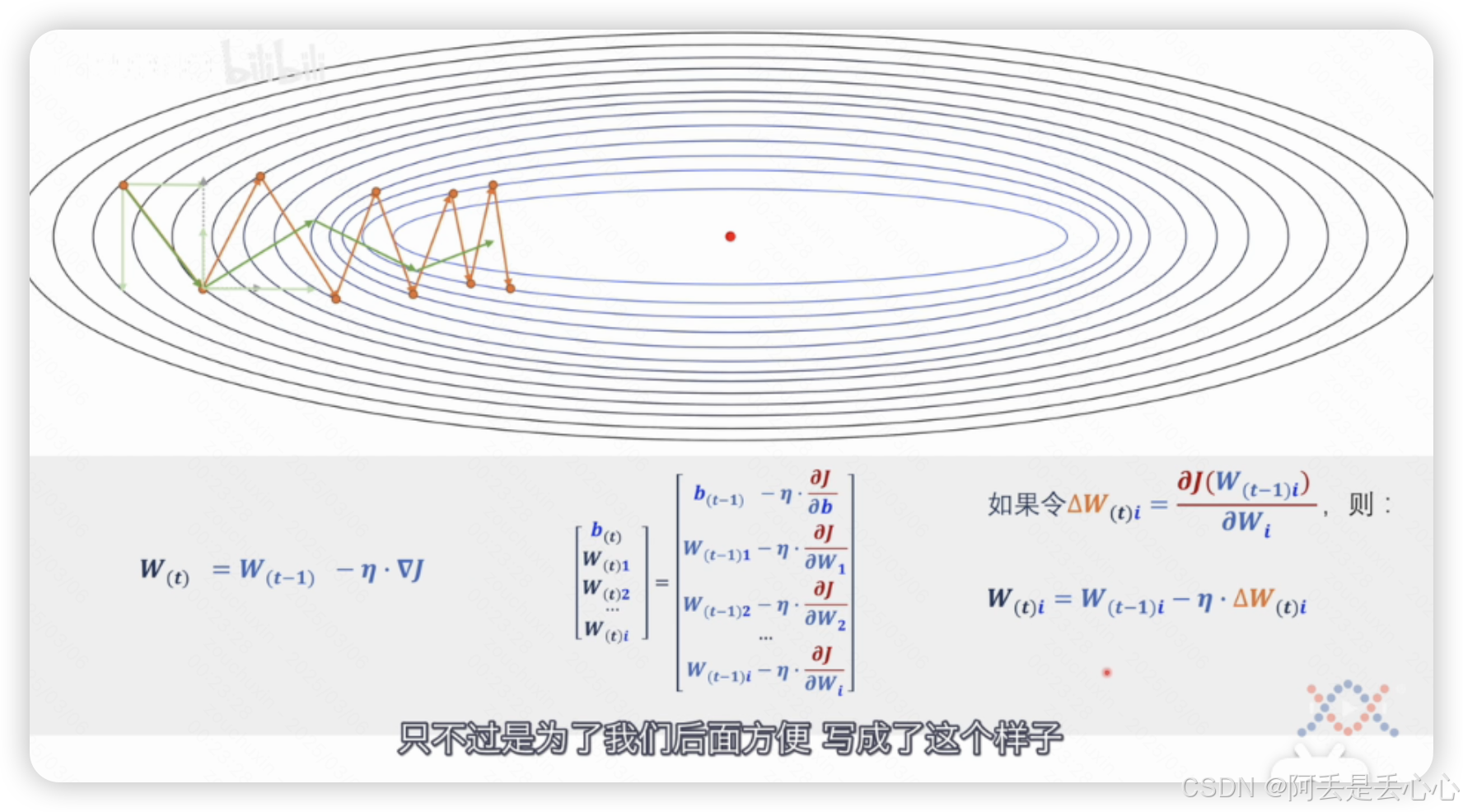
 (4)动量梯度下降算法（momentum）

把纵轴上来回震荡的分量减弱以及在横轴上加速

 

(5)adagrad算法——让学习率自适应调整

Adagrad优化算法就是在每次使用一个 batch size 的数据进行参数更新的时候，算法计算所有参数的梯度，那么其想法就是对于每个参数，初始化一个变量 s 为 0，然后每次将该参数的梯度平方求和累加到这个变量 s 上，然后在更新这个参数的时候，学习率就变为

 

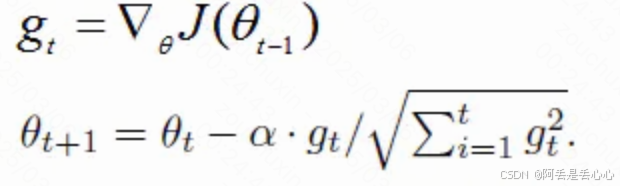
gt表示第t时间步的梯度（向量，包含各个参数对应的偏导数，gt,i表示第i个参数t时刻偏导数）

gt2表示第t时间步的梯度平方（向量，由gt各元素自己进行平方运算所得，即Element-wise）

与SGD的核心区别在于计算更新步长时，增加了分母：梯度平方累积和的平方根。

Adagrad 的核心想法就是，如果一个参数的梯度一直都非常大，那么其对应的学习率就变小一点，防止震荡，而一个参数的梯度一直都非常小，那么这个参数的学习率就变大一点，使得其能够更快地更新，这就是Adagrad算法加快深层神经网络的训练速度的核心

(6)RMSProp

 

优势：能够克服AdaGrad梯度急剧减小的问题，在很多应用中都展示出优秀的学习率自适应能力。尤其在不稳定(Non-Stationary)的目标函数下，比基本的SGD、Momentum、AdaGrad表现更良好。

(7)Adam

 综合考虑动量梯度下降和RMSProp

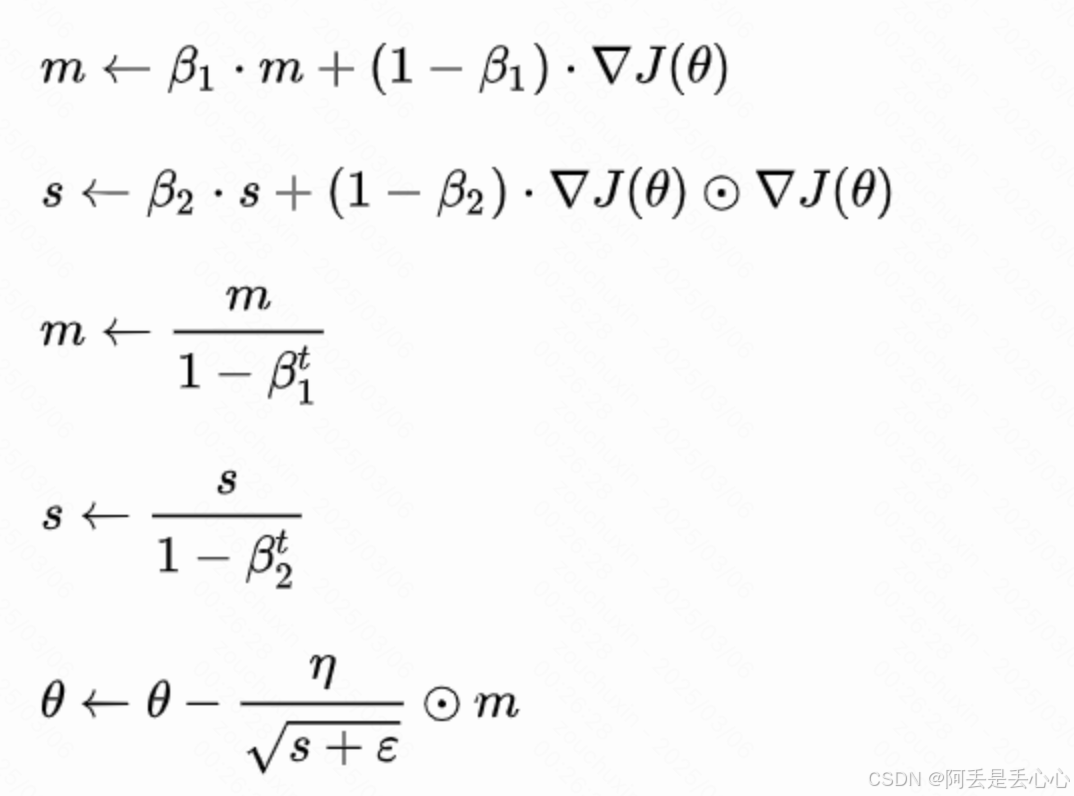
到现在为止，我们已经知道了神经网络是什么以及什么网络的参数是如何变化的，后续我们再简单讲讲神经网络的实现、怎么判断神经网络的训练效果等基础概念就进入到深度学习模块啦～敬请期待叭

# 神经网络 # 人工智能 # 深度学习
Logo
DeepSeek技术社区

欢迎加入DeepSeek 技术社区。在这里，你可以找到志同道合的朋友，共同探索AI技术的奥秘。

更多推荐

cover

企业微信如何使用deepseek-最简单的方法

avatar DeepSeek技术社区
cover

第38次CCF-CSP认证——月票发行（chatgpt5 vs deepseekv3.1）

avatar DeepSeek技术社区

deepseek 关闭思考，在ollama中，在代码中

deepseek 关闭思考，在ollama中，在代码中

avatar DeepSeek技术社区