经典文献阅读之--KISS-Matcher(快速且稳健的点云注册)

我们的目标是对齐两个无序的体素化点云，体素大小为vvv，即源点云PPP和目标点云QQQ。为此，我们在两个点云之间建立对应关系，随后进行稳健估计，以抑制异常值的不良影响。形式上，假设通过匹配获得的第kkk对（或第kkk个对应关系）由3D点ai∈Pa_i \in Pai∈P和3D点bj∈Qb_j \in Qbj∈Q组成。那么，第kkkbjRaitϵij(1)bjRaitϵij1其中R∈S。

Hermit_Rabbit

6184人浏览 · 2025-04-21 19:32:04

Hermit_Rabbit · 2025-04-21 19:32:04 发布

0. 简介

3D点云配准是一项估计两个部分重叠的点云之间相对位姿的基本问题，与基于迭代最近点（ICP）的方法不同，这类方法具有较小的收敛区域，且仅当初始估计较好的情况下才会收敛到理想解。而全局配准旨在无需初始估计的前提下估计相对位姿。因此，全局配准广泛用于应用场景，通常提供初始对齐，以使ICP方法收敛到更优的解。

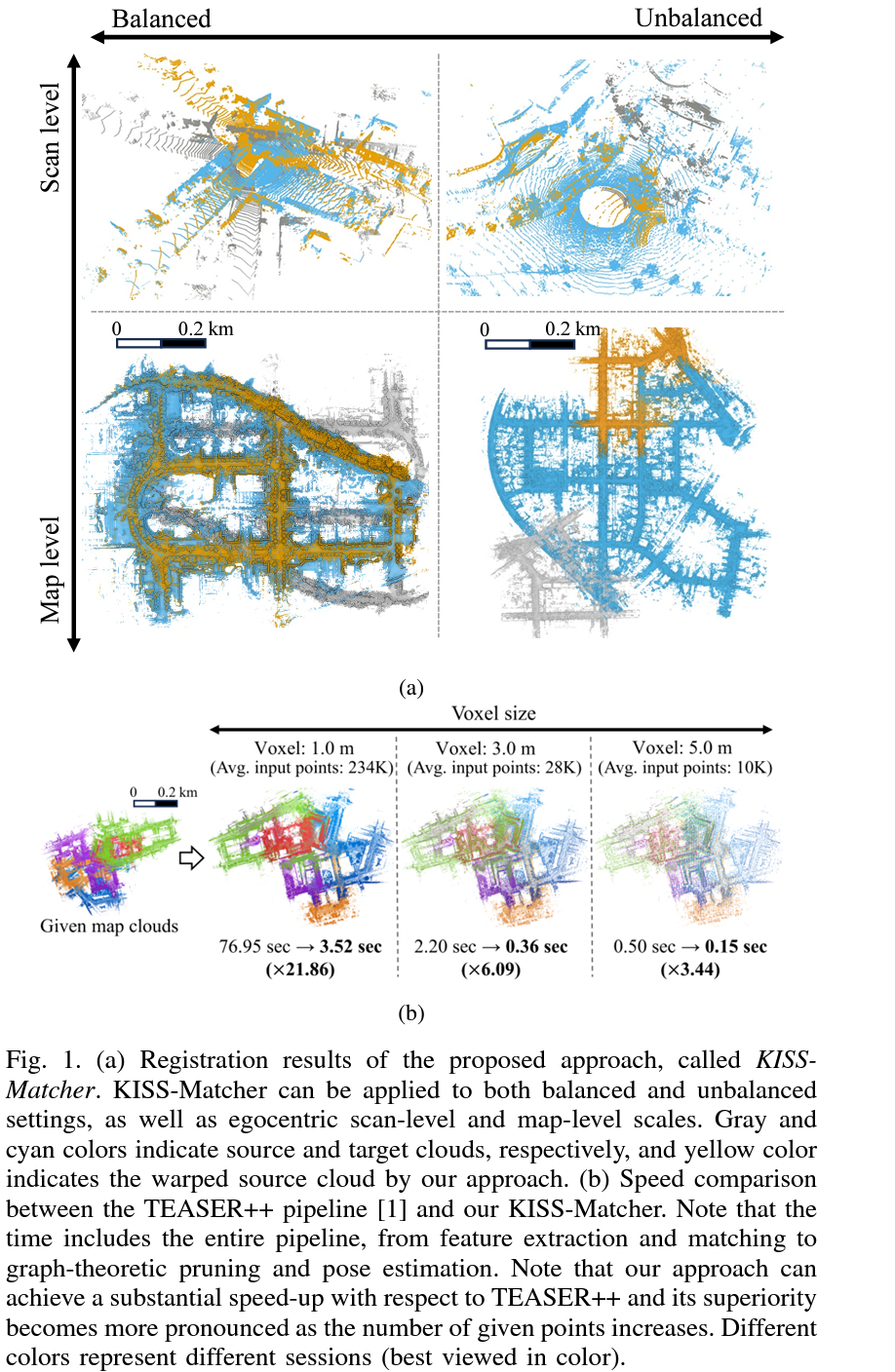
在这里插入图片描述

图1. (a) 所提出方法的注册结果，称为KISS-Matcher。KISS-Matcher可以应用于平衡和不平衡的设置，以及自我中心的扫描级别和地图级别。灰色和青色分别表示源点云和目标点云，黄色表示通过我们的方法变形后的源点云。(b) TEASER++工作流程[1]与我们的KISS-Matcher之间的速度比较。请注意，时间包括整个工作流程，从特征提取和匹配到图论修剪和姿态估计。我们的方案在速度上相较于TEASER++实现了显著的加速，且随着给定点数的增加，其优势愈加明显。不同的颜色代表不同的实验会话（最佳效果请在彩色显示下查看）。

先前的研究往往专注于提升特定组件的性能（例如，特征提取、基于图论的修剪或姿态求解器），而忽略了整个配准流程的实时性和更广泛的适用性。尤其是，尽管近期基于深度学习的方法在未训练的场景中展现了较好的泛化能力，一些基于学习的方法忽略了数据预处理所需的时间，或依赖于大量的随机采样一致性（RANSAC）迭代，这些迭代可能耗时数秒甚至数十秒。《KISS-Matcher: Fast and Robust Point Cloud Registration Revisited》将这些模块结合成一个完整、用户友好且即用的工作流程。经过大量实验验证，同时代码已经发布在Github上了。

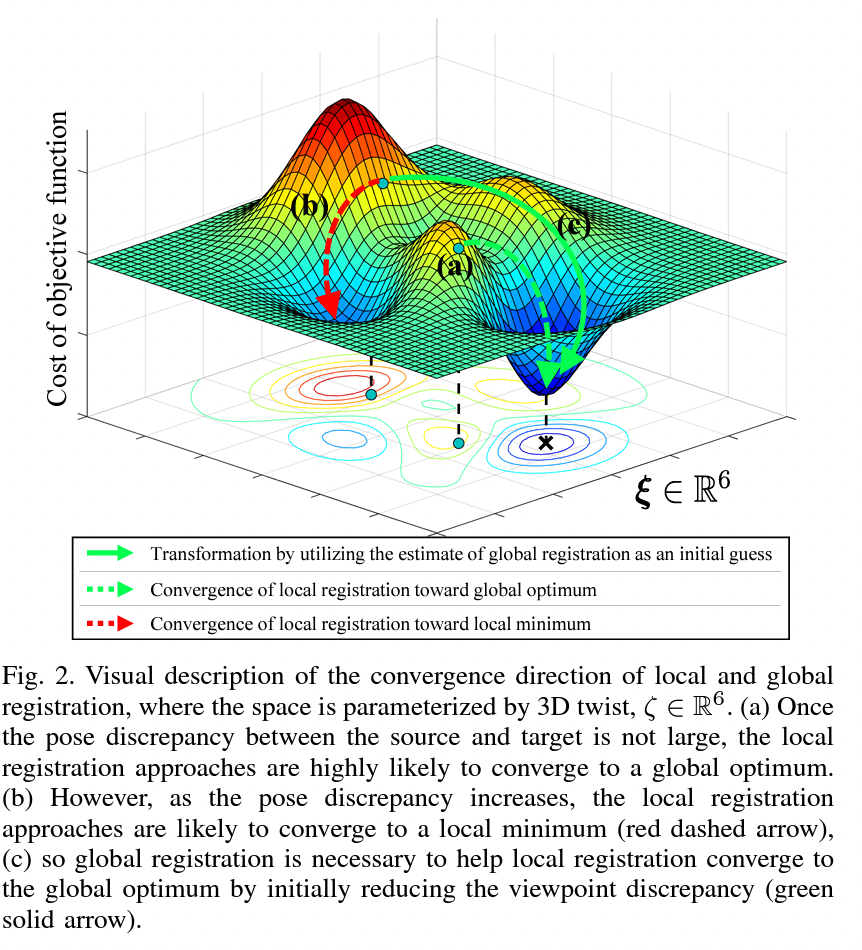
在这里插入图片描述

图2. 局部和全局注册的收敛方向的视觉描述，其中空间由3D扭转参数化， $\zeta \in \mathbb{R}^6$ 。(a) 当源点云和目标点云之间的姿态差异不大时，局部注册方法很可能会收敛到全局最优解。(b) 然而，随着姿态差异的增加，局部注册方法可能会收敛到局部最小值（红色虚线箭头），© 因此，全局注册是必要的，它通过最初减少视角差异（绿色实线箭头）来帮助局部注册收敛到全局最优解。

1. 主要贡献

本文介绍的KISS-Matcher[1]是一种快速且可扩展的配准系统，将每个配准管道组件的最新进展结合到一个多功能且可随时使用的C++库中。遵循KISS-ICP的理念，重点提升系统的适用性，减少对传感器特定假设或繁琐参数调整的依赖。

从整体角度处理配准问题，特别针对TEASER++管道[2]中的问题进行了改进，尤其是其在地图级匹配场景下无法处理大量对应关系的情况。为了解决这一问题：

通过提出Faster-PFH加速了经典的手工设计描述符——快速点特征直方图(FPFH)
采用基于k-core的图论修剪技术来拒绝错误的对应关系。

系统在速度上比TEASER++快了数倍，同时实现了类似的性能（如图1(b)所示）。

2. KISS-MATCHER：稳健、快速且可扩展的抗干扰匹配

在本节中，我们将介绍KISS-Matcher的流程，该流程遵循图3所示的基于特征的抗干扰注册的典型流程。我们的KISS-Matcher由四个组件组成：a) 几何抑制，b) 基于Faster-PFH的特征提取和初始匹配，c) 基于k-core的图论抗干扰拒绝，d) 基于渐进非凸性的非最小求解器。

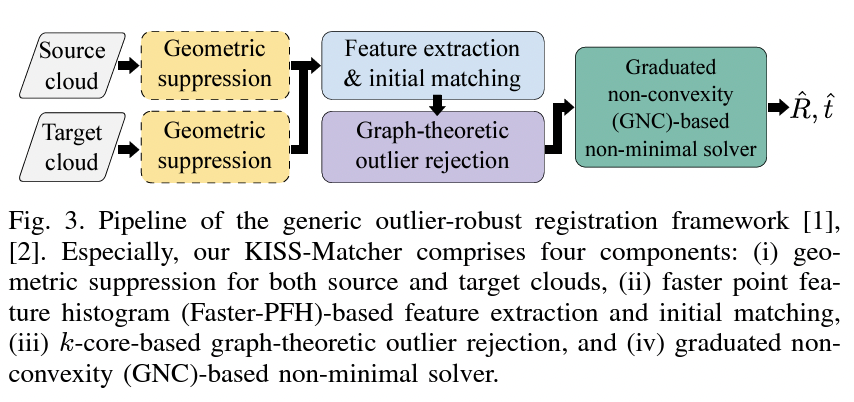
在这里插入图片描述

图3. 通用抗干扰注册框架的流程图 [1], [2]。特别地，我们的KISS-Matcher由四个组件组成：(i) 源点云和目标点云的几何抑制，(ii) 基于快速点特征直方图（Faster-PFH）的特征提取和初始匹配，(iii) 基于k-core的图论抗干扰拒绝，以及 (iv) 基于渐进非凸性（GNC）的非最小求解器。

3. 问题定义

我们的目标是对齐两个无序的体素化点云，体素大小为 $v$ ，即源点云 $P$ 和目标点云 $Q$ 。为此，我们在两个点云之间建立对应关系，随后进行稳健估计，以抑制异常值的不良影响。形式上，假设通过匹配获得的第 $k$ 对（或第 $k$ 个对应关系）由3D点 $a_i \in P$ 和3D点 $b_j \in Q$ 组成。那么，第 $k$ 个测量可以建模为：

$b_j = R a_i + t + \epsilon_{i,j} \tag{1}$

其中 $\in SO(3)$ 是相对旋转矩阵， $\in \mathbb{R}^3$ 是平移向量， $\epsilon_{i,j} \in \mathbb{R}^3$ 是测量噪声。最后，设初始对应关系集为 $A$ ，我们的目标函数可以表示为：

$\hat{R}, \hat{t} = \arg\min_{R \in SO(3), t \in \mathbb{R}^3} \sum_{(i,j) \in A/ \hat{O}} (\hat{\rho} \|b_j - R a_i - t\|_2), \tag{2}$

其中 $\rho(\cdot)$ 表示一种稳健损失函数，旨在抑制由错误对应关系（或异常值）引起的不良大误差，而 $\hat{O}$ 表示在优化之前经过预过滤的粗大异常值（例如，通过图论抗干扰修剪，如图3所示）。因此，式(2)旨在在对异常值具有稳健性的情况下，估计源点云和目标点云之间的相对姿态。

4. 作为预处理步骤的几何抑制

正如杨等人所报道的[1]，环境中重复模式所导致的对应关系，例如地面、天花板或建筑物平面墙壁上的点，会产生大量的异常值（例如，当许多不同点对在平面上被错误地识别为匹配时），这会妨碍从公式(2)中获得的位姿估计的质量。因此，如果这些点能够被轻易检测到，它们应该在预处理步骤中被过滤掉，以使我们的方法更加稳健[2]；我们将这一预处理称为几何抑制。因此，这种几何抑制不仅防止后续步骤收敛到不良解，还通过提前拒绝冗余和非独特的点来增强特征的独特性。此外，它还可以通过减少点云的数量显著加快后续步骤的速度。为了保持一般性，我们继续用 $P$ 和 $Q$ 表示经过几何抑制处理后的过滤点云。

5. Faster-PFH：提升FPFH速度

接下来，我们需要在点云P和Q之间提取和匹配特征。为此，我们提出了FasterPFH，这是一种更高效的FPFH变体[31]，同时保持了相似的性能。如图4(a)所示，FPFH计算的过程主要遵循三个步骤：（i）使用半径 $r_{\text{normal}}$ 内的邻近点进行每个点的法线估计；（ii）在查询点与邻近点之间提取角特征，使用FPFH半径 $r_{\text{FPFH}}$ ，随后基于角特征的分布计算简化的PFH（SPFH）特征；（iii）通过对邻近点的SPFH进行加权平均来计算FPFH特征[31]。然而，现有的FPFH特征提取在实时应用中可能不太适用；例如，将FPFH应用于由64通道LiDAR传感器捕获的体素化源点云和目标点云，其点数范围从10K到30K，即使在Intel® Core™ i9-13900 CPU上使用多线程，处理时间也超过0.1秒；见第IV.E节。特别地，FPFH存在两个计算瓶颈。首先，计算效率低下源于邻近点搜索的多次执行（即三轮半径搜索，在图4(a)中称为“RS with $r_{\text{normal}}$ ”或“RS with $r_{\text{FPFH}}$ ”）。其次，由于其解耦方案没有彻底检查法线估计是否可靠，SPFH和FPFH的提取在法线向量不可靠的点上不必要地进行，导致邻近FPFH特征的表达能力下降。为了解决这两个问题，我们采用了两种策略。首先，为了减少不必要的计算成本，我们仅对每个点执行一次半径 $r_{\text{FPFH}}$ 的邻近点搜索，并重用结果。然后，基于 $r_{\text{normal}} \leq r_{\text{FPFH}}$ 的事实，我们从邻近搜索的输出 $P_{\text{FPFH}}$ 中对法线估计进行下采样，得到 $P_{\text{normal}}$ （即 $P_{\text{normal}} \subset P_{\text{FPFH}}$ ）。其次，对于每个点，如果 $P_{\text{FPFH}}$ 的基数小于 $\tau_{\text{num}}$ 或线性度（即 $\frac{\lambda_1 - \lambda_2}{\lambda_1}$ ，其中 $\lambda_1, \lambda_2, \lambda_3$ 是通过主成分分析（PCA）从 $P_{\text{normal}}$ 中获得的三个特征值，满足 $\lambda_1 \geq \lambda_2 \geq \lambda_3$ ）高于 $\tau_{\text{lin}}$ ，则该点在角特征、SPFH和FPFH特征的计算中被排除。在这里， $\tau_{\text{num}}$ 和 $\tau_{\text{lin}}$ 是用户定义的阈值。通过这样做，我们仅为可靠的点生成描述符，类似于半直接方法[55]。然后，通过使用Faster-PFH的输出，建立初始对应集A，进行互匹配（或互惠测试[4]）。因此，我们不仅可以生成更可靠的描述符，还可以通过预先拒绝可能导致异常值的潜在点来降低计算成本。最终，我们在单线程和多线程情况下的速度分别提高了约4.5倍和2.4倍，同时保持了性能。

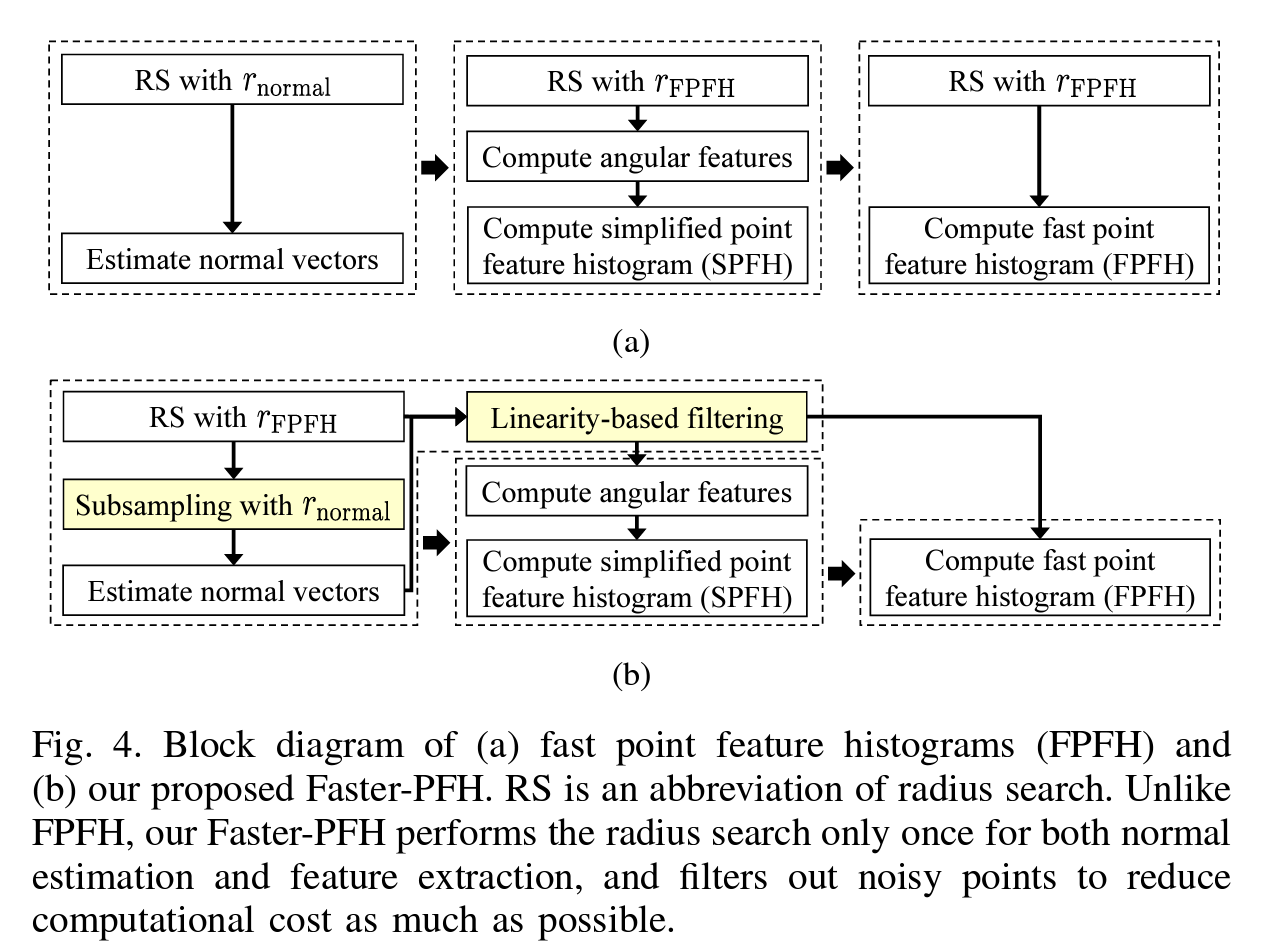
在这里插入图片描述

图4. (a) 快速点特征直方图（FPFH）和 (b) 我们提出的Faster-PFH的框图。RS是半径搜索的缩写。与FPFH不同，我们的Faster-PFH仅对法线估计和特征提取执行一次半径搜索，并过滤掉噪声点，以尽可能降低计算成本。

6. 基于k-core的图论异常值修剪

接下来，我们解决一个经验性问题，即现有的TEASER++管道在对应点数量增加时变得极为缓慢，这种情况在子图级或地图级配准中经常发生，从而阻碍了管道的可扩展性。这种减速是由于TEASER++中的最大团内点选择（MCIS），其时间复杂度呈指数级增长，并且一旦对应点数量超过500-1000点，速度就会显著变慢。在这里，我们使用基于k-core的图论修剪方法[54]来规避指数复杂度。更具体地说，我们的修剪过程主要遵循两个步骤，以尽可能多地拒绝虚假对应点。

首先，以 $A$ 作为输入，我们利用成对不变性 [4]，[54] 的概念，这是一种针对点云配准的 n-不变性的专门版本 [54]。形式上，考虑 $A$ 中的两个内点对应关系，其索引分别为 $(i, j)$ 和 $i^′, j^′)$ 。假设内点噪声是有界的（例如， $ϵ_{i,j}\| ≤ β$ 和 $ϵ_{i′,j′}\| ≤ β$ ，其中 $β > 0$ 是用户定义的阈值），可以使用以下不等式（见 [1] 的推导）来建立内点对应关系必须满足的条件：

$\|b_j - b_{j^′}\| - \|a_i - a_{i^′}\| ≤ 2β. \tag{3}$

基于 (3)，我们将测量关系表示为兼容性图 $G (V, E)$ ，其中顶点集 $V$ 中的每个顶点代表 A 中的一个对应关系对，而边集 $E$ 中的每条边在两个顶点之间建立，如果它们对应的测量满足一致性关系 (3)。其次，通过寻找大量相互一致的测量，我们可以识别潜在的内点并过滤掉明显的异常值。特别是，一旦构建了 $G (V, E)$ ，我们就寻找图的最大 k-core，以获得一组大量兼容的测量。因此，不兼容的对应关系被丢弃作为异常值（这就是 (2) 中的集合 $\hat{O}$ ）。正如 Shi 等人 [54] 所示，寻找最大 k-core 的性能接近 MCIS，但其时间复杂度为线性 $O (∣ V ∣ + ∣ E ∣)$ 。相比之下，识别任意图中最大团的最快算法的复杂度为 $O(1.1888^{|V|})$ [56]–[58]，其复杂度随着 $∣ V ∣$ 的增加而呈指数增长。

除了利用基于 k-core 的修剪外，我们还采用压缩稀疏行（CSR）格式，而不是原始 TEASER++ 流水线中使用的邻接矩阵格式，因为 CSR 格式在处理大型稀疏图时更为节省内存。然而，如果给定的对应关系过多，减速是不可避免的，因为我们的方法也会经历运行时间的线性增加。为了解决这个问题，在执行上述两个步骤之前，我们首先选择具有最低描述符距离比的前 $N τ$ 个对应关系，这一选择受到比率测试 [59] 的启发。通过这样做，这种基于比率的过滤提前拒绝了特征区分度低的配对，确保对应关系的数量不超过 $N τ$ 。

7. 基于渐进非凸性的非最小求解器

需要注意的是，尽管图论异常值修剪通常会过滤掉明显的异常值，但在集合 $\setminus \hat{O}$ 中可能仍会残留一些异常值。因此，即使 $\hat{O}$ 被拒绝，我们仍然使用渐进非凸性（GNC） [29] 求解器，通过求解 (2) 来稳健地估计相对姿态。GNC 基于求解器的一个有用特性是，它允许我们通过检查最终内点集的基数 $I_{\text{final}}$ 是否足够大来判断配准是否有效 [1]。通过这样做，与其他求解器（例如基于学习的方法）不同，我们的 GNC 基于求解器能够过滤掉失败和潜在不准确的配准结果，从而提高配准精度（见图 5(a)）。

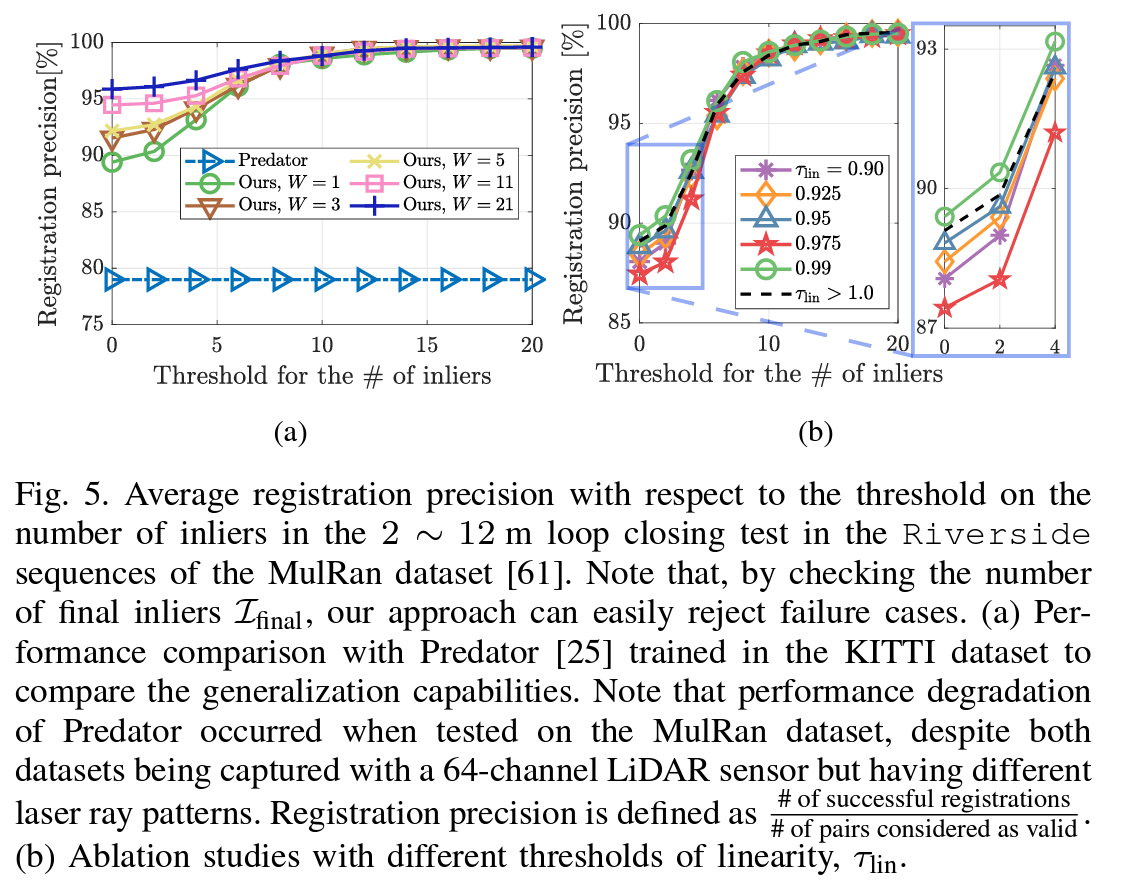
在这里插入图片描述

图5. 在MulRan数据集[61]的Riverside序列中，2至12米环闭测试中，关于内点数量阈值的平均配准精度。请注意，通过检查最终内点数量 $I_{\text{final}}$ ，我们的方法能够轻松地拒绝失败案例。(a) 与在KITTI数据集上训练的Predator [25]的性能比较，以评估其泛化能力。值得注意的是，尽管两个数据集均使用64通道LiDAR传感器捕获，但由于激光束模式不同，Predator在MulRan数据集上的性能有所下降。配准精度定义为成功配准的数量与被视为有效的配对数量之比。 (b) 不同线性阈值 $\tau_{\text{lin}}$ 的消融研究。