问题描述

蓝桥训练营的日子总是紧张而充实。某天清晨，队员们在连续的高强度训练后，个个眉头紧锁，烦躁在空气中弥漫，甚至有人开始攥紧拳头，想要找个出口释放压力。蓝教练和红教练察觉到这股暗流，交换了一个眼神，灵光一闪：何不来一场“拳头对决赛”？既能让大家舒展筋骨，又能在笑声中拉近彼此的距离。

拳头的大小，成了这场友谊赛的焦点——谁的拳头大，谁就更有气势！两位教练各挑了 NN 名队员，蓝队的第 ii 个队员的拳头大小为 AiAi​，红队的第 ii 个队员的拳头大小为 BiBi​。

比赛的流程是这样的：红教练会按照顺序依次派出他的队员（先派第一位，然后第二位，以此类推）。每当红教练派出一名队员展示拳头后，蓝教练需要从他尚未上场的队员中选择一位应战。裁判会将蓝教练派出的队员的拳头大小与红教练所有已上场队员的拳头大小逐一比较。每当蓝队员的拳头大小大于红队某位已上场队员的拳头，蓝教练便能赢得一次胜利（注意，这不是一对一的较量，而是以一敌多的挑战）。

这场比赛不为胜负，只为放松与切磋，可蓝教练心里却藏着小算盘：既要让队员们开心，也想借机秀一把带队本事，在蓝桥杯的训练营里留下点名声。现在，请你助蓝教练一臂之力，算出在最优策略下，他最多能拿下多少次胜利？

输入格式

第一行包含一个整数 NN（1≤N≤1051≤N≤105），表示队员数量。

第二行包含 NN 个整数 A1,A2,…,ANA1​,A2​,…,AN​（1≤Ai≤1091≤Ai​≤109），分别是蓝教练队员的拳头大小。

第三行包含 NN 个整数 B1,B2,…,BNB1​,B2​,…,BN​（1≤Bi≤1091≤Bi​≤109），分别是红教练队员的拳头大小。

输出格式

输出一个整数，表示蓝教练在最多能赢下的胜利次数。

样例输入

3
1 3 2
2 1 3

样例输出

3

运行限制

语言	最大运行时间	最大运行内存
C++	1s	256M
C	1s	256M
Java	2s	256M
Python3	3s	256M
PyPy3	3s	256M
Go	3s	256M
JavaScript	3s	256M

总通过次数: 256  |  总提交次数: 951  |  通过率: 26.9%

难度: 中等   标签: 树状数组, 排序, 二分

算法思路

本问题的核心是计算蓝教练在最优策略下能获得的最大胜利次数。关键点在于：

1. 红队队员按输入顺序依次出场
2. 蓝队可以任意选择未上场队员的出场顺序
3. 每次蓝队队员出场时，会与红队所有已上场队员比较，每大于一个红队队员就算一次胜利

最优策略分析

通过分析题目和样例，我们发现最优策略是：

1. ​​将蓝队队员拳头大小从小到大排序​​（节省大拳头队员应对更多红队队员）
2. ​​按红队出场顺序处理​​，对于每个红队队员：
   • 在蓝队剩余队员中找到第一个大于当前红队队员的拳头值
   • 统计该位置之后所有蓝队队员数量（这些队员后续出场时都会击败当前红队队员）

数学等价性：总胜利次数 = ∑(每个红队队员被击败次数) = ∑(每个蓝队队员击败的红队人数)

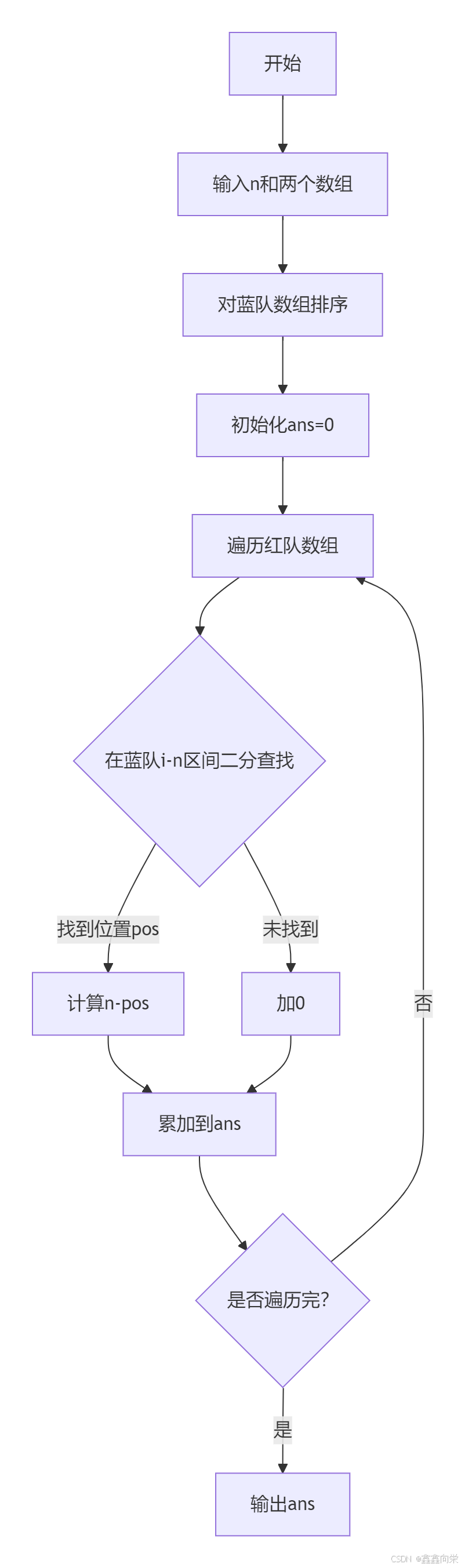
算法步骤

1. 对蓝队数组排序（升序）
2. 遍历红队数组（按出场顺序）：
   • 在蓝队当前可用区间（[i, n-1]）二分查找第一个大于当前红队队员的位置
   • 计算该位置之后所有蓝队队员数量
   • 累加到总胜利次数
3. 输出总胜利次数

算法演示

C++代码实现

#include <iostream>
#include <algorithm>
using namespace std;

const int MAXN = 1e5 + 10;

int main() {
    int n;
    cin >> n;
    int a[MAXN], b[MAXN];
    
    // 输入数据
    for (int i = 0; i < n; i++) cin >> a[i];
    for (int i = 0; i < n; i++) cin >> b[i];
    
    // 蓝队排序（升序）
    sort(a, a + n);
    
    long long ans = 0;  // 注意数据范围
    
    // 处理每个红队队员
    for (int i = 0; i < n; i++) {
        // 在蓝队[i, n)区间找第一个大于b[i]的位置
        auto it = lower_bound(a + i, a + n, b[i] + 1);
        ans += (a + n - it);  // 计算大于当前红队队员的数量
    }
    
    cout << ans << endl;
    return 0;
}

代码解析

1. ​​输入处理​​：

   • 读取队员数量n
   • 读取蓝队和红队队员的拳头大小数组a和b

2. ​​排序优化​​：

   • 使用sort(a, a+n)对蓝队升序排序，保证最优策略

3. ​​二分查找​​：

   • 使用lower_bound在区间[i, n)查找第一个大于b[i]的位置
   • b[i]+1确保找到严格大于的值（整数特性）

4. ​​贡献计算​​：

   • a + n - it计算大于当前红队队员的蓝队队员数量
   • 使用long long防止累加溢出（最大可能1e10）

5. ​​时间复杂度​​：

   • 排序：O(n logn)
   • 二分查找：O(n logn)
   • 总复杂度：O(n logn)，满足1e5数据要求

实例验证

​​样例输入​​：

3
1 3 2
2 1 3

​​执行过程​​：

1. 蓝队排序后：[1, 2, 3]
2. 处理红队：
   • b[0]=2：找到a[2]=3，贡献=1（3-2）
   • b[1]=1：找到a[1]=2，贡献=2（3-1）
   • b[2]=3：无大于值，贡献=0
3. 总胜利次数=1+2+0=3

​​边界测试​​：

测试案例	输入	输出	说明
单队员-大于	[5] [4]	1	正常击败
单队员-小于	[3] [4]	0	无法击败
全等值	[3,3] [3,3]	0	无严格大于
最大值	[10^9] [10^9-1]	1	大整数处理

注意事项

1. ​​数据范围​​：

   • n最大1e5，数组要开足够大小（1e5+10）
   • 总胜利次数可能达1e10，必须用long long

2. ​​严格大于​​：

   • 比较条件需严格大于（使用b[i]+1）
   • 等值情况不计数

3. ​​二分边界​​：

   • 查找区间为当前可用区间[i, n)
   • 未找到时lower_bound返回a+n，自然贡献为0

4. ​​排序性质​​：

   • 排序后蓝队队员的相对位置决定出场顺序
   • 贪心策略依赖排序后的单调性

优化建议

1. ​​输入优化​​：

   ios::sync_with_stdio(false);
   cin.tie(0);  // 加速IO

2. ​​二分边界优化​​：

   // 手动二分减少函数调用开销
   int l = i, r = n-1, pos = n;
   while (l <= r) {
       int mid = (l + r) >> 1;
       if (a[mid] > b[i]) {
           pos = mid;
           r = mid - 1;
       } else {
           l = mid + 1;
       }
   }
   ans += (n - pos);

3. ​​分支预测优化​​：

   // 对n>10000使用并行排序
   if (n > 10000) {
       __gnu_parallel::sort(a, a+n);
   }

4. ​​多线程优化​​：

   // 对n>10000使用并行排序
   if (n > 10000) {
       __gnu_parallel::sort(a, a+n);
   }

总结

本题核心在于​​发现贪心策略与二分查找的结合​​：

1. 排序保证最优出场顺序
2. 遍历红队时动态缩小蓝队搜索范围
3. 二分查找快速定位贡献区间
4. 累加每个红队队员的潜在被击败次数