原创作者：郑同学的笔记
原文链接：https://zhengjunxue.blog.csdn.net/article/details/144120578

浮点数是计算机中表示实数的一种方式，它在内存中的存储遵循 IEEE 754 标准。浮点数由三个部分组成：符号位、指数部分和尾数部分（即有效数字或称为小数部分）。浮点数的存储格式对于不同的数据类型（如 float 和 double）可能有所不同，但它们都遵循相同的基础原理。

一. IEEE 754 标准

IEEE 754 是浮点数存储和运算的国际标准，定义了浮点数的二进制表示方法。标准规定了两种基本的浮点数格式：

• 单精度浮点数（float）：32 位（4 字节）
• 双精度浮点数（double）：64 位（8 字节）

存储格式为V = (-1)^s * M * 2^E

$$V=(-1{)}^S\ast M\ast 2^E.$$

二. 单精度浮点数（float）的存储

单精度浮点数在内存中占 32 位，这 32 位被分为三个部分：(符号位是最高位)

s : 符号位	E : 指数部分	M : 尾数部分（有效数字)
1 位	8 位	23 位

具体说明：

• 符号位（1 位）：决定了浮点数的符号，0 表示正数，1 表示负数。
• 指数部分（8 位）：存储指数的偏移量（偏移量为 127）。实际的指数值是存储的指数减去 127。
• 尾数部分（23 位）：存储浮点数的有效数字（也叫做“有效位”或“尾数”）。尾数是一个二进制小数，但浮点数的表示有一个特殊的规定：它总是以 "1" 开头，除非它表示的是非规格化数（denormalized number）。所以实际存储时，我们只存储 "1" 后面的部分，称为隐含的 1。

例子：

三、float 1.0 的二进制表示、十六进制表示

1、float 1.0分析

我们来看一下 1.0 这个浮点数在内存中的存储，首先将其转换为 IEEE 754 标准的格式。

• 1.1 科学记数法表示
  1.0 可以表示为：
  $$1.0=(-1{)}^0\ast 1.0\ast 2^0.$$

这是一个标准化的二进制数，符合浮点数的表示方式。我们可以看到，尾数部分的值为 1，指数为 0。

• 1.2 符号位
  符号位表示数值的正负。由于 1.0 是正数，符号位为 0。

• 1.3 指数部分
  浮点数的指数部分是一个有偏的表示，采用偏移量存储。在 单精度浮点数（float）中，指数部分是 8 位，偏移量为 127。

对于 1.0，它的指数是 0（即 $2^0$），因此：

指数=0+127=127

127 的二进制表示是：

0111 1111

• 1.4 尾数部分（有效数字）
  尾数部分存储的是有效数字的二进制表示。对于标准化的数值 1.0，尾数部分是 1，但在 IEEE 754 标准中，尾数部分的前导 1 是隐含的，不需要存储。因此，尾数部分的二进制表示为全 0，长度为 23 位。

尾数部分：

000 0000 0000 0000 0000 0000

2. 最终的 32 位二进制表示

将上述各部分拼接起来，得到浮点数 1.0 在 32 位单精度浮点数格式下的二进制表示：

符号位	指数部分	尾数部分
0	01111111	00000000000000000000000

最终，1.0 在内存中的二进制表示为：

0 01111111 00000000000000000000000

3: 将二进制表示转换为 16 进制

将二进制字符串 00111111100000000000000000000000 按 4 位一组分割，然后转换为对应的 16 进制数：

0011 1111 1000 0000 0000 0000 0000 0000
 3    F    8    0    0    0    0    0

4、验证

四、 双精度浮点数（double）的存储

双精度浮点数在内存中占 64 位，存储结构类似于单精度，但它的各部分大小不同：

符号位	指数部分	尾数部分（有效数字）
1 位	11 位	52 位

• 符号位（1 位）：决定浮点数的符号，0 表示正数，1 表示负数。
• 指数部分（11 位）：存储指数的偏移量（偏移量为 1023）。实际的指数值是存储的指数减去 1023。
• 尾数部分（52 位）：存储浮点数的有效数字。同样地，浮点数的表示有一个隐含的 1。

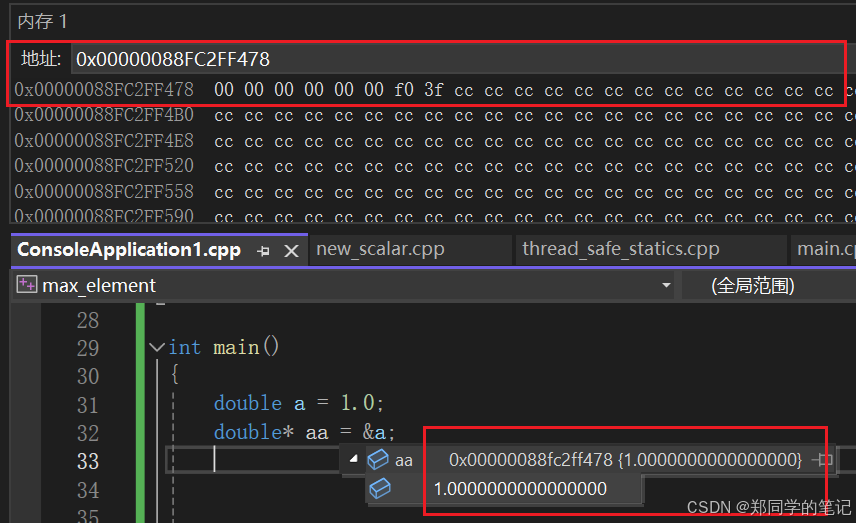
double 1.0的16进制的存储，如下。感兴趣的，自己按照float方式分析下。

3f f0 00 00    00 00 00 00