数据结构——一元多项式计算器
首先,这是数据结构老师布置的实验结构的作业,课上的时候没有怎么听,但是由于这个实验老师要现删代码让我们补,所以,糊弄肯定是不那么简单的,代码有点多,背代码真的不太现实,所以打算自己写,参考别人的代码,边理解边写PS:代码参考了AI的思路(deepseek的生成的代码放在了结尾),和AI的部分代码首先,先要了解一下什么是一元多项式(如下图)如上图,有一个未知变量,变量旁边有系数和指数,具体概念可以去
需要了解的概念:结构体指针和链表
目录
首先,这是数据结构老师布置的实验结构的作业,课上的时候没有怎么听,但是由于这个实验老师要现删代码让我们补,所以,糊弄肯定是不那么简单的,代码有点多,背代码真的不太现实,所以打算自己写,参考别人的代码,边理解边写
PS:代码参考了AI的思路(deepseek的生成的代码放在了结尾),和AI的部分代码
首先,先要了解一下什么是一元多项式(如下图)
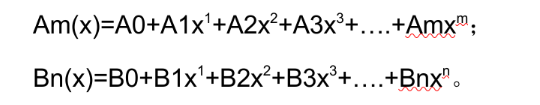
如上图,有一个未知变量,变量旁边有系数和指数,具体概念可以去查数学课本上查一下
如果要把这个一元多项式在控制台输出出来,就是以下的形式:x^4 - 3 x^2 + 5
废话不多说那就开始写把
1.要求
创建两个一元多项式
对两个多项式进行加、减、乘的运算;
对多项式进行升幂和降幂的输出;
x^4 - 3 x^2 + 5 (降幂)
5 + x^4 - 3 x^2( 升幂)
2.所需函数
因为程序有些复杂,所以就避免不了写亿些函数,函数已经在下面罗列出来了
typedef struct poly
{
int coef; //系数
int expo; //指数
struct poly* next; //指向下一个项(结构体的指针)
}*Polynomial;
//宏定义项(起一个别名,目的是区分 多项式 和 项)
#define Item Polynomial
//这两个指针都是 struct poly 结构体的指针,一个是项的指针,一个是多项式的头指针
Polynomial CreatePolynomial();//创建多项式
void freePolynomial(Polynomial head);//释放多项式各个项的指针的内存
Item CreateItem(int coef,int expo); //创建项
void InserItem(Polynomial head,int coef,int expo);//向多项式中插入项
void printPolynomial(Polynomial head);//打印多项式
void DecPrintPolynomial(Polynomial head);//降序打印
Polynomial AddPolynomial(Polynomial head_a, Polynomial head_b);//多项式相加
Polynomial MinusPolynomial(Polynomial head_a, Polynomial head_b);//多项式相减
Polynomial MultiplyPolynomials(Polynomial head_a, Polynomial head_b);//多项式相减
共有九个函数,分别按照使用顺序进行排列出来了
3.整体思路
一元多项式的创建运用到了链式表的思路,所以就用到了指针,别问问为什么非得用指针,不用实验不符合要求而且肯定会不好写
为了更加直观的展示,我画了一张图作为参考

如图,我们要用到三个变量:系数(coef)、指数(expo)、指向下一个项(Item)的指针,其中系数和指数我们要用到整形变量,此外还有一个指向地址的指针,同时存多种变量类型的数据就要用到结构体,结构体的定义如下
struct poly
{
int coef; //系数
int expo; //指数
struct poly* next; //指向下一个项(结构体的指针)
};
不过因为我们在写代码的时候会多次用到结构体(也就是Item)指针,所以我们在定义的时候给它起几个别名
typedef struct poly
{
int coef; //系数
int expo; //指数
struct poly* next; //指向下一个项(结构体的指针)
}*Polynomial;
#define Item Polynomial
//这两个指针都是 struct poly 结构体的指针,一个是项的指针,一个是多项式的头指针
这样可以少写很多 “*”
Item 是项的英文
Polynomial 是多项式的英文
4.执行过程
可以参考main函数中的内容
int main()
{
/*
两个多项式指针,a,b
result是多项式进行运算后的指针
*/
Polynomial poly_a=NULL,poly_b=NULL,result=NULL;
int choice;
while (1) {
printf("\n多项式运算菜单:\n");
printf("1. 输入多项式A和B\n");//要先进行操作1,添加多项式
printf("2. 加法运算\n");
printf("3. 减法运算\n");
printf("4. 乘法运算\n");
printf("5. 打印多项式\n");
printf("6. 降序打印多项式\n");
printf("请选择操作:");
scanf("%d", &choice);
switch (choice) {
case 1:
if (poly_a != NULL) freePolynomial(poly_a);
//添加多项式前要先检查多项式是否已经存在,如果存在,那就释放内存
if (poly_b != NULL) freePolynomial(poly_b);
poly_a=CreatePolynomial();//添加多项式,赋的值为多项式的头指针
printf("请输入第二个多项式");
poly_b=CreatePolynomial();
break;
case 2:
result=AddPolynomial(poly_a,poly_b);
printPolynomial(result);
DecPrintPolynomial(result);
break;
case 3:
result=MinusPolynomial(poly_a,poly_b);
printPolynomial(result);
DecPrintPolynomial(result);
break;
case 4:
result=MultiplyPolynomials(poly_a,poly_b);
printPolynomial(result);
DecPrintPolynomial(result);
break;
case 5:
printPolynomial(poly_a);
printPolynomial(poly_b);
break;
case 6:
DecPrintPolynomial(poly_a);
DecPrintPolynomial(poly_b);
break;
default:
break;
}
}
}
首先定义三个Polynomial变量,就是指向结构体的指针,先定义为空,之后再让它们等于多项式的头指针(通过创建多项式和进行运算操作后)
1.创建多项式
参考我之前画的那张图,我们进行的是链式表的操作,所以我们要的其实就是一个(头)指针,这个(头)指针起的是一个定位的作用,可以把这个头指针理解成一个 “门”?
Polynomial CreatePolynomial()//创建多项式
{
Polynomial head=CreateItem(0,0);
//创建多项式的头指针,头指针其定位的作用
//作用只是指向下一个项(结构体)的地址(位置)
int coef,expo;
while(1)//这个循环是用来创建项的,两个两个的输入,碰到0 0就会终止
{
#ifdef LOGOUT
printf("请输入 系数 指数 ,然后回车,指数(输入0 0结束):");
#endif
scanf("%d %d",&coef,&expo);//不过输入的时候还是要判断一下的,看看那些能输入
if (coef == 0 && expo == 0) break;//终止输入符
if(coef !=0)//因为系数如果输入零就没有意义了
InserItem(head,coef,expo);//项插入的函数
#ifdef LOGOUT
else
printf("系数为0.跳过");
#endif
}
printf("输入完成一个多项式");
return head;
}
我们首先要创建一个头指针,并对它进行初始化,所谓初始化,就是给你定义的结构体变量手动分配内存。头指针其实和其他项的指针没有任何本质区别都是结构体指针,怎么手动分配可以自行搜索一下(需要用到malloc函数),头指针的系数和指数随便定义,因为用不到,要的只是那个指向下一个项的指针
Item CreateItem(int coef,int expo)//创建项,创建头指针
{
Item NewItem=(Item)malloc(sizeof(struct poly));//分配内存
if(NewItem==NULL)
{
printf(" 内存分配失败\n");
}
NewItem->coef=coef;
NewItem->expo=expo;
NewItem->next=NULL;
#ifdef LOGOUT
printf("项创建成功\n");
#endif
return NewItem;
}
这个函数同样适用于创建项
2.插入项
接下来就要开始插入项了,这个插入项的函数的功能很强大,以至于老师说我们模块化做得不行
它可以在插入的时候自动检测,最终让你插入的项进行升幂排序
void InserItem(Polynomial head,int coef,int expo)//向一个多项式中插入项
{
//定义变量的时候有点问题,pre应该是head,cur应该是head->next
//凑合看吧
Polynomial pre=NULL;//指向上一个结构体的指针
Polynomial cur=head;//指向当前结构体的指针
//因为head这个指针指向的结构体的数据(系数、指数)不会使用,要的只是head中指向下一个结构体的地址
//所以一开始插入的逻辑就是让head的next指针指向下一个结构体地址
while(cur->next!= NULL && cur->next->expo < expo)
//插入的时候会按指数的大小进行排序,如果插入项的指数比较大,就会往后排
//每次插入的时候都是从head指针开始遍历的,所以只要检测出cur->next->expo不小于插入项的系数就会跳出循环
{
pre=cur;//指针整体后移动
cur=cur->next;
}
#ifdef LOGOUT
printf("当前指数%d\n",cur->expo);//查看从那个指数后面插入
#endif
if(cur->next!= NULL && cur->next->expo == expo)//如果发现插入的项的指数一样,那就
{
pre=cur;
cur=cur->next;
cur->coef+=coef;//让系数相加就行了
#ifdef LOGOUT
printf("系数合并成功\n");
#endif
if(cur->coef==0)//系数正负抵消变为0
{
pre->next=cur->next;//跳过这一一个位置
free(cur);//并释放当前地址的内存
}
}
else//只要是指数不相等,无论指数过大还是过小,都用这种思路
{
if(cur->next)//下一个位置有地址说明插入的指针是偏小的
{
pre=cur->next;//存一下原来下一个结构体的地址,防止地址丢失
cur->next=CreateItem(coef,expo);//插入进去然后重新指一下
cur=cur->next;//后移一位
cur->next=pre;//然后让下一个位置指向原来的地址
}
else//下一个位置没有地址,说明是向最后一个位置后面插的
{
cur->next=CreateItem(coef,expo);//就正常指就行
//cur=cur->next;
}
}
}
插入项要考虑的情况有,项的正常插入,同指数项系数相加,系数相加为0的情况
3.其他函数
剩下的函数还有,升幂降幂打印,多项式的加、减、乘运算,相比较于插入函数都简单到💥了,
5.总体代码
我写的
#include <stdio.h>
#include <stdlib.h>
#define LOGOUT
//定义宏,用来控制一些输出,注释掉会少很多输出
/*
* 这个宏牵扯到这个语句
* #ifdef LOGOUT
* --要执行的语句
* #endif
* 意思就是如果通过#define定义了LOGOUT(不需要给值)
* 就执行其中的语句
* 与#ifdef同语法的有#ifndef(如果没有定义)
* 就比如这个头文件的第一行和最后一行
*/
typedef struct poly
{
int coef; //系数
int expo; //指数
struct poly* next; //指向下一个项(结构体的指针)
}*Polynomial;
//宏定义项(起一个别名,目的是区分 多项式 和 项)
#define Item Polynomial
//这两个指针都是 struct poly 结构体的指针,一个是项的指针,一个是多项式的头指针
Item CreateItem(int coef,int expo)//创建项
{
Item NewItem=(Item)malloc(sizeof(struct poly));//分配内存
if(NewItem==NULL)
{
printf(" 内存分配失败\n");
}
NewItem->coef=coef;
NewItem->expo=expo;
NewItem->next=NULL;
#ifdef LOGOUT
printf("项创建成功\n");
#endif
return NewItem;
}
void InserItem(Polynomial head,int coef,int expo)//向一个多项式中插入项
{
//定义变量的时候有点问题,pre应该是head,cur应该是head->next
//凑合看吧
Polynomial pre=NULL;//指向上一个结构体的指针
Polynomial cur=head;//指向当前结构体的指针
//因为head这个指针指向的结构体的数据(系数、指数)不会使用,要的只是head中指向下一个结构体的地址
//所以一开始插入的逻辑就是让head的next指针指向下一个结构体地址
while(cur->next!= NULL && cur->next->expo < expo)
//插入的时候会按指数的大小进行排序,如果插入项的指数比较大,就会往后排
//每次插入的时候都是从head指针开始遍历的,所以只要检测出cur->next->expo不小于插入项的系数就会跳出循环
{
pre=cur;//指针整体后移动
cur=cur->next;
}
#ifdef LOGOUT
printf("当前指数%d\n",cur->expo);//查看从那个指数后面插入
#endif
if(cur->next!= NULL && cur->next->expo == expo)//如果发现插入的项的指数一样,那就
{
pre=cur;
cur=cur->next;
cur->coef+=coef;//让系数相加就行了
#ifdef LOGOUT
printf("系数合并成功\n");
#endif
if(cur->coef==0)//系数正负抵消变为0
{
pre->next=cur->next;//跳过这一一个位置
free(cur);//并释放当前地址的内存
}
}
else//只要是指数不相等,无论指数过大还是过小,都用这种思路
{
if(cur->next)//下一个位置有地址说明插入的指针是偏小的
{
pre=cur->next;//存一下原来下一个结构体的地址
cur->next=CreateItem(coef,expo);//插入进去然后重新指一下
cur=cur->next;//后移一位
cur->next=pre;//然后让下一个位置指向原来的地址
}
else//下一个位置没有地址,说明是向最后一个位置后面插的
{
cur->next=CreateItem(coef,expo);//就正常指就行
//cur=cur->next;
}
}
}
void freePolynomial(Polynomial head)//释放多项式各个项的指针的内存
{
Polynomial current = head->next;
while (current != NULL)//看下一个位置是否有地址
{
Polynomial temp = current;
current = current->next;
free(temp);//有的话就释放
}
free(head);//顺带把头指针也释放了
}
Polynomial CreatePolynomial()//创建多项式
{
Polynomial head=CreateItem(0,0);
//创建多项式的头指针,头指针其定位的作用
//作用只是指向下一个项(结构体)的地址(位置)
int coef,expo;
while(1)//这个循环是用来创建项的,两个两个的输入,碰到0 0就会终止
{
#ifdef LOGOUT
printf("请输入 系数 指数 ,然后回车,指数(输入0 0结束):");
#endif
scanf("%d %d",&coef,&expo);//不过输入的时候还是要判断一下的,看看那些能输入
if (coef == 0 && expo == 0) break;//终止输入符
if(coef !=0)//因为系数如果输入零就没有意义了
InserItem(head,coef,expo);//项插入的函数
#ifdef LOGOUT
else
printf("系数为0.跳过");
#endif
}
printf("输入完成一个多项式");
return head;
}
void printPolynomial(Polynomial head)//打印多项式
{
if(head->next==NULL)//先判断多项式是否为空,不为空才能打印
{
printf("多项式为空\n");
return;
}
while(head->next)//遍历打印
{
if(head->next->expo)//指数为不为0就把指数打印出来
printf("%dx^%d",head->next->coef,head->next->expo);
else//为0就只打印系数
printf("%d",head->next->coef);
head=head->next;//后移一位
if(head->next !=NULL && head->next->coef > 0 )printf("+");//打印"+"号
}
printf("打印完毕\n");
}
void DecPrintPolynomial(Polynomial head)//降序打印
{
//思路就是通过while循环先看多项式存了多少个数据
//然后两层for循环,外层是看需要打印多少个数据,内层是要打印的数据的位置
Polynomial p=head;
int index=0;
while (p->next)//根据下一个位置是存数据来判断
{
index++;
p=p->next;
}
p=head;//重置
int Index=index;
//printf("index=%d\n",index);
for (int i = 0; i < Index; i++)//几个数据循环几次,打印几次
{
for (int j = index; j >0; j--)//因为是降幂打印,所以是递减的
{
p=p->next;
}
if(p->coef > 0 && Index != index)printf("+");
//第一次打印数据前不需要写"+"号
//系数小于零就更不用打印"+"号,负数自带符号
if(p->expo)//老样子
printf("%dx^%d",p->coef,p->expo);
else
printf("%d",p->coef);
index--;
p=head;//重置
}
printf("降幂打印结束\n");
}
Polynomial AddPolynomial(Polynomial head_a, Polynomial head_b)//多项式相加
{
//总体思路就是把两个多项式的 项 挨个插入(有自己写的插入函数)到一个新的多项式中
Polynomial result=CreateItem(0,0);
Polynomial pa=head_a;
Polynomial pb=head_b;
while(pa->next)//插到底
{
pa=pa->next;
//printf("A的%d %d\n",pa->coef,pa->expo);
InserItem(result,pa->coef,pa->expo);
}
while(pb->next!=NULL)//插到底
{
pb=pb->next;
InserItem(result,pb->coef,pb->expo);
//printf("B的%d %d\n",pb->coef,pb->expo);
}
return result;//返回
}
Polynomial MinusPolynomial(Polynomial head_a, Polynomial head_b)//多项式相减
{
//和相加一样,就是把其中一个多项式的项在插入的时候把系数变为其相反数
Polynomial result=CreateItem(0,0);
Polynomial pa=head_a;
Polynomial pb=head_b;
while(pa->next)
{
pa=pa->next;
//printf("A的%d %d\n",pa->coef,pa->expo);
InserItem(result,pa->coef,pa->expo);
}
while(pb->next!=NULL)
{
pb=pb->next;
InserItem(result,-(pb->coef),pb->expo);//系数取反
//printf("B的%d %d\n",pb->coef,pb->expo);
}
return result;
}
Polynomial MultiplyPolynomials(Polynomial head_a, Polynomial head_b)//多项式相乘
{
//一个多项式的各个项与另一个多项式的各个项进行乘法运算
Polynomial result=CreateItem(0,0);
Polynomial pa=head_a;
Polynomial pb=head_b;
while(pa->next)//嵌套while循环
{
pa=pa->next;
while(pb->next)
{
pb=pb->next;
int coef=pa->coef*pb->coef;
int expo=pa->expo+pb->expo;
InserItem(result,coef,expo);
}
pb=head_b;//重置一下
}
return result;
}
int main()
{
/*
* 两个多项式指针,a,b
* result是多项式进行运算后的指针
*/
Polynomial poly_a=NULL,poly_b=NULL,result=NULL;
int choice;
while (1) {
printf("\n多项式运算菜单:\n");
printf("1. 输入多项式A和B\n");//要先进行操作1,添加多项式
printf("2. 加法运算\n");
printf("3. 减法运算\n");
printf("4. 乘法运算\n");
printf("5. 打印多项式\n");
printf("6. 降序打印多项式\n");
printf("请选择操作:");
scanf("%d", &choice);
switch (choice) {
case 1:
if (poly_a != NULL) freePolynomial(poly_a);
//添加多项式前要先检查多项式是否已经存在,如果存在,那就释放内存
if (poly_b != NULL) freePolynomial(poly_b);
poly_a=CreatePolynomial();//添加多项式,赋的值为多项式的头指针
printf("请输入第二个多项式\n");
poly_b=CreatePolynomial();
break;
case 2:
result=AddPolynomial(poly_a,poly_b);
printPolynomial(result);
DecPrintPolynomial(result);
break;
case 3:
result=MinusPolynomial(poly_a,poly_b);
printPolynomial(result);
DecPrintPolynomial(result);
break;
case 4:
result=MultiplyPolynomials(poly_a,poly_b);
printPolynomial(result);
DecPrintPolynomial(result);
break;
case 5:
printPolynomial(poly_a);
printPolynomial(poly_b);
break;
case 6:
DecPrintPolynomial(poly_a);
DecPrintPolynomial(poly_b);
break;
default:
break;
}
}
}
这是运行结果
多项式运算菜单:
1. 输入多项式A和B
2. 加法运算
3. 减法运算
4. 乘法运算
5. 打印多项式
6. 降序打印多项式
请选择操作:1
1 1 2 2 0 0
输入完成一个多项式请输入第二个多项式
2 3 4 5 0 0
输入完成一个多项式
多项式运算菜单:
1. 输入多项式A和B
2. 加法运算
3. 减法运算
4. 乘法运算
5. 打印多项式
6. 降序打印多项式
请选择操作:5
1x^1+2x^2打印完毕
2x^3+4x^5打印完毕多项式运算菜单:
1. 输入多项式A和B
2. 加法运算
3. 减法运算
4. 乘法运算
5. 打印多项式
6. 降序打印多项式
请选择操作:6
2x^2+1x^1降幂打印结束
4x^5+2x^3降幂打印结束多项式运算菜单:
1. 输入多项式A和B
2. 加法运算
3. 减法运算
4. 乘法运算
5. 打印多项式
6. 降序打印多项式
请选择操作:2
1x^1+2x^2+2x^3+4x^5打印完毕
4x^5+2x^3+2x^2+1x^1降幂打印结束多项式运算菜单:
1. 输入多项式A和B
2. 加法运算
3. 减法运算
4. 乘法运算
5. 打印多项式
6. 降序打印多项式
请选择操作:3
1x^1+2x^2-2x^3-4x^5打印完毕
-4x^5-2x^3+2x^2+1x^1降幂打印结束多项式运算菜单:
1. 输入多项式A和B
2. 加法运算
3. 减法运算
4. 乘法运算
5. 打印多项式
6. 降序打印多项式
请选择操作:4
2x^4+4x^5+4x^6+8x^7打印完毕
8x^7+4x^6+4x^5+2x^4降幂打印结束
AI(deepseek的)
#include <stdio.h>
#include <stdlib.h>
typedef struct Term {
int coef;
int exp;
struct Term *next;
} Term;
typedef Term* Polynomial;
// 创建新项
Term* createTerm(int coef, int exp) {
Term* newTerm = (Term*)malloc(sizeof(Term));
if (newTerm == NULL) {
printf("内存分配失败\n");
exit(1);
}
newTerm->coef = coef;
newTerm->exp = exp;
newTerm->next = NULL;
return newTerm;
}
// 插入项并合并同类项
void insertTerm(Polynomial head, int coef, int exp) {
if (coef == 0) return; // 忽略零系数项
Term* prev = head;
Term* current = head->next;
while (current != NULL && current->exp < exp) {
prev = current;
current = current->next;
}
if (current != NULL && current->exp == exp) {
current->coef += coef;
if (current->coef == 0) {
prev->next = current->next;
free(current);
}
} else {
Term* newTerm = createTerm(coef, exp);
newTerm->next = current;
prev->next = newTerm;
}
}
// 输入多项式
Polynomial inputPolynomial() {
Polynomial head = createTerm(0, 0); // 头结点
int coef, exp;
printf("输入多项式各项的系数和指数(输入0 0结束):\n");
while (1) {
scanf("%d %d", &coef, &exp);
if (coef == 0 && exp == 0) break;
insertTerm(head, coef, exp);
}
return head;
}
// 释放多项式内存
void freePolynomial(Polynomial head) {
Term* current = head->next;
while (current != NULL) {
Term* temp = current;
current = current->next;
free(temp);
}
free(head);
}
// 复制多项式
Polynomial copyPolynomial(Polynomial src) {
Polynomial dst = createTerm(0, 0);
Term* s = src->next;
Term* d = dst;
while (s != NULL) {
d->next = createTerm(s->coef, s->exp);
d = d->next;
s = s->next;
}
return dst;
}
// 多项式相加
Polynomial addPolynomials(Polynomial a, Polynomial b) {
Polynomial result = createTerm(0, 0);
Term* pa = a->next;
Term* pb = b->next;
while (pa != NULL || pb != NULL) {
if (pa == NULL) {
insertTerm(result, pb->coef, pb->exp);
pb = pb->next;
} else if (pb == NULL) {
insertTerm(result, pa->coef, pa->exp);
pa = pa->next;
} else if (pa->exp < pb->exp) {
insertTerm(result, pa->coef, pa->exp);
pa = pa->next;
} else if (pa->exp > pb->exp) {
insertTerm(result, pb->coef, pb->exp);
pb = pb->next;
} else {
int sum = pa->coef + pb->coef;
if (sum != 0) {
insertTerm(result, sum, pa->exp);
}
pa = pa->next;
pb = pb->next;
}
}
return result;
}
// 多项式相减
Polynomial subtractPolynomials(Polynomial a, Polynomial b) {
Polynomial negB = copyPolynomial(b);
Term* p = negB->next;
while (p != NULL) {
p->coef = -p->coef;
p = p->next;
}
Polynomial result = addPolynomials(a, negB);
freePolynomial(negB);
return result;
}
// 多项式相乘
Polynomial multiplyPolynomials(Polynomial a, Polynomial b) {
Polynomial result = createTerm(0, 0);
Term* pa = a->next;
while (pa != NULL) {
Term* pb = b->next;
while (pb != NULL) {
int coef = pa->coef * pb->coef;
int exp = pa->exp + pb->exp;
insertTerm(result, coef, exp);
pb = pb->next;
}
pa = pa->next;
}
return result;
}
// 反转链表用于降序输出
Polynomial reversePolynomial(Polynomial head) {
Polynomial newHead = createTerm(0, 0);
Term* current = head->next;
while (current != NULL) {
Term* next = current->next;
current->next = newHead->next;
newHead->next = current;
current = next;
}
free(head);
return newHead;
}
// 打印多项式
void printPolynomial(Polynomial head, int isDescending) {
if (head->next == NULL) {
printf("0\n");
return;
}
if (isDescending) {
head = reversePolynomial(copyPolynomial(head));
}
Term* current = head->next;
int isFirst = 1;
while (current != NULL) {
if (!isFirst) {
if (current->coef > 0) printf(" + ");
else printf(" - ");
} else {
if (current->coef < 0) printf("-");
}
int absCoef = abs(current->coef);
if (absCoef != 1 || current->exp == 0) {
printf("%d", isFirst ? abs(current->coef) : absCoef);
}
if (current->exp > 0) {
printf("x");
if (current->exp > 1) printf("^%d", current->exp);
}
isFirst = 0;
current = current->next;
}
printf("\n");
if (isDescending) {
freePolynomial(head);
}
}
// 主菜单
int main() {
int choice;
Polynomial polyA = NULL, polyB = NULL, result = NULL;
while (1) {
printf("\n多项式运算菜单:\n");
printf("1. 输入多项式A和B\n");
printf("2. 加法运算\n");
printf("3. 减法运算\n");
printf("4. 乘法运算\n");
printf("0. 退出\n");
printf("请选择操作:");
scanf("%d", &choice);
if (choice == 0) break;
if (choice != 1 && (polyA == NULL || polyB == NULL)) {
printf("请先输入多项式A和B!\n");
continue;
}
switch (choice) {
case 1:
if (polyA != NULL) freePolynomial(polyA);
if (polyB != NULL) freePolynomial(polyB);
printf("输入多项式A:\n");
polyA = inputPolynomial();
printf("输入多项式B:\n");
polyB = inputPolynomial();
break;
case 2:
result = addPolynomials(polyA, polyB);
printf("\n加法结果(升幂):");
printPolynomial(result, 0);
printf("加法结果(降幂):");
printPolynomial(result, 1);
freePolynomial(result);
break;
case 3:
result = subtractPolynomials(polyA, polyB);
printf("\n减法结果(升幂):");
printPolynomial(result, 0);
printf("减法结果(降幂):");
printPolynomial(result, 1);
freePolynomial(result);
break;
case 4:
result = multiplyPolynomials(polyA, polyB);
printf("\n乘法结果(升幂):");
printPolynomial(result, 0);
printf("乘法结果(降幂):");
printPolynomial(result, 1);
freePolynomial(result);
break;
default:
printf("无效选择!\n");
}
}
if (polyA != NULL) freePolynomial(polyA);
if (polyB != NULL) freePolynomial(polyB);
return 0;
}
框架很像,但又不是那么像
6.自言自语
今个儿给老师汇报实验,呃......,老师说我讲的过于细了,啧,然后还教育(指导)了我一顿,多项唉,上一次听到这样的话还是在我大一的时候,果然是真心的,也是今天突然发现我的汇报能力还是没有什么长进,总是啰嗦而且还卡壳,我确实不适合演讲,回汇报,有稿子也一样,因为就算有稿子我也还是会一意孤行,边讲边改,为什么呢,因为书面语和口语还是有很大不一样的。
老师说让我以后再向ta汇报一次,不让我现写代码,说相信我的代码😎,挺好的。
文章以后再改改
更多推荐








 已为社区贡献1条内容
已为社区贡献1条内容






所有评论(0)