源自: AINLPer（每日干货分享！！）
编辑: ShuYini
校稿: ShuYini
时间: 2025-4-13

更多：>>>>专注大模型/AIGC、学术前沿的知识分享！

引言

位置编码是大模型架构的重要组成部分。本文从位置编码的起源开始介绍，详细介绍Transformer位置编码、相对位置编码、重点介绍了旋转位置编码RoFE、ALiBI位置编码等，最后介绍DeepSeek位置编码，希望能够帮你对位置编码有一个详细的了解。文章结构如下：

• 位置编码起源
• 基础位置编码
• Transformer位置编码
• 相对位置编码
• 旋转位置编码（RoFE）
• ALiBi位置编码
• DeepSeek位置编码

位置编码起源

对任何语言来说，句子中词汇的顺序和位置都是非常重要的。它们定义了语法，从而定义了句子的实际语义。RNN结构本身就涵盖了单词的顺序，RNN按顺序逐字分析句子，这就直接在处理的时候整合了文本的顺序信息。

Transformer模型抛弃了RNN、CNN作为序列学习的基本模型，完全采用注意力机制取而代之。对于一个输入句子，其单词不再是顺序输入，而是一次性输入一个序列中的所有词，依靠纯粹的自注意力机制来捕获词之间的联系，直接对这个序列整体进行特征变换。

这种改变相比传统的序列模型可以节约大量的计算成本。这同时也带了一个比较重要的问题：因为Attention矩阵计算存在位置不变性，导致无法捕获Token之间的位置关系！

可能有小伙伴理解为什么位置编码的重要性。举个简单的例子如下：

我喜欢你→对应Token分别为：我、喜欢、你
你喜欢我→对应Token分别为：你、喜欢、我

假设每个Token的向量维度为4，那么上面序列的长度为3，对应的代码如下：

import torch
import torch.nn.functional as F
d = 4 # 词嵌入维度
l = 3 # 句子长度
q = torch.randn(1,d) # 我
k = torch.randn(l,d) # 我喜欢你
v = torch.randn(l,d) # 我喜欢你
print(q)
print(k)
print(v)
orig_attn = F.softmax(q@k.transpose(1,0),dim=1)@v

# 调转位置
k_shift = k[[2,1,0],:] # 你喜欢我
v_shift = v[[2,1,0],:] # 你喜欢我
shift_attn = F.softmax(q@k_shift.transpose(1,0),dim=1)@v_shift
print('我爱你:',orig_attn)
print('你爱我:',shift_attn)

我爱你: tensor([[-0.8736, -0.5525, -0.0170, -0.5777],
                [-0.8572, -0.5168, -0.0525, -0.5672],
                [-1.2609,  0.0334, -0.0458, -1.1972]])
你爱我: tensor([[-0.8736, -0.5525, -0.0170, -0.5777],
                [-0.8572, -0.5168, -0.0525, -0.5672],
                [-1.2609,  0.0334, -0.0458, -1.1972]])

可以发现如果q是“我”，无论句子是“我喜欢你”还是“你喜欢我”，其注意力输出都是完全一致的。这说明在没有位置序列信息的情况下，改变词语顺序的句子实际语义是不一样的，但是注意力输出相同，无法准确建模。这就是为什么Transformer需要添加位置编码。

想给模型一些位置信息，一个方案是在每个单词中添加一条关于其在句子中位置的信息。我们称之为“信息片段”，即位置编码。这里再给个正式点的位置编码定义：位置编码（Positional Embedding）是一种用于处理序列数据的技术，被用来表示输入序列中的单词位置。

基础位置编码

上面介绍了位置编码的起源，那么怎么添加位置编码呢？

第一个可能想到的方法是为每个时间步添加一个[0-1]范围内的数字，其中0表示第一个单词，1表示最后一个单词。但这样会存在一个问题：无法计算出特定范围内有多少个单词。换句话说，时间步长在不同句子中的含义不一致。如下图：
另一个可能的想法是为每个时间步按一定步长线性分配一个数字。也就是说，第一个单词是“1”，第二个单词是“2”第三个单词是“3”，依此类推。这种方法的问题在于，随着句子变长，这些值可能会变得特别大，并且我们的模型在实际应用中可能会遇到比训练时更长的句子，此外，我们的模型可能会忽略某些长度的样本（比如Bert模型支持最长序列长度为512），这会损害模型的泛化。

以上两种方法，其实就是所谓的绝对位置编码。但是其实理想情况下，位置编码需要满足以下几个要求：

• 每个时间步都有唯一的编码。
• 在不同长度的句子中，两个时间步之间的距离应该一致。
• 模型不受句子长短的影响，并且编码范围是有界的。（不会随着句子加长数字就无限增大）
• 必须是确定性的。

Transformer位置编码

有很多文章说将Transformer的正弦位置编码归属于绝对位置编码，这是绝对真确的！你可能会好奇：通过正余弦变换，可以推导出其含有相对位置，为什么不叫相对位置编码呢？其中主要原因是：在输入Embedding+位置Embedding，计算Attention的时候，由于矩阵变换的原因，会破坏掉这种相对位置信息。

在Transformer原始论文中，作者提出的编码是一种简单但是很精妙的方法，满足上述所有标准。首先，它不是单独某个数字，它是一个𝑑维向量，其中包含句子中特定位置的信息。其次，这种编码并没有集成到模型本身中，该向量用于为每个单词提供有关其在句子中位置的信息。也就是说，其修改了模型的输入，添加了单词的顺序信息。如下图红框所示：

Transformer位置编码原理

设 $t$ 为输入句子中期望的位置，$\overrightarrow{p_t}\in {\mathbb{R}}^d$ 为其对应的编码向量，$d$ 为编码维度（其中 $d{\equiv }_{2}0$，这里表示的意思是：$d$ 除2之后余数为0）那么 $f:\mathbb{N}\to {\mathbb{R}}^d$ 将是生成输出位置向量 $\overrightarrow{p_t}$ 的函数，定义如下：

$${\overrightarrow{p_t}}^{(i)}=f(t{)}^{(i)}:=\{\begin{array}{ll}\sin ({\omega }_k\cdot t),& \text{如果 }i=2k\\ \cos ({\omega }_k\cdot t),& \text{如果 }i=2k+1\end{array}$$

其中：

$${\omega }_k=\frac{1}{10000^{2k/d}}$$

从函数定义中可以得出，频率随着向量维度的增加而减小。因此，它在波长上形成了从 $2\pi$ 到 $10000\cdot 2\pi$ 的几何级数。你也可以将位置嵌入 $\overrightarrow{p_t}$ 想象为一个包含每个频率的正弦和余弦对的向量（注意 ：$d$ 需要能被2整除）：

$$\overrightarrow{p_t}={\left[\begin{array}{c}\sin ({\omega }_1\cdot t)\\ \cos ({\omega }_1\cdot t)\\ \sin ({\omega }_2\cdot t)\\ \cos ({\omega }_2\cdot t)\\ ⋮\\ \sin ({\omega }_{d/2}\cdot t)\\ \cos ({\omega }_{d/2}\cdot t)\end{array}\right]}_{d\times 1}$$

Transformer位置编码图例解释

此时，你可能好奇：正余弦组合怎么能代表一个位置信息呢？其实很简单，假设你想用二进制格式表示一个数字：

可以看到不同位置上的数字交替变化。最后一位数字每次都会0、1交替；倒数第二位置上00，11相互交替一次，倒数第三个位置上0000，1111相互交替，以此类推。（第 𝑖 位置上 2𝑖 个数据交替一次）。

但对于浮点数来说，使用二进制值是对空间的浪费，所以可以用正弦函数代替。事实上，正弦函数也能表示出二进制那样的交替。此外随着正弦函数频率的降低，也可以达到上图红色位到橙色位交替频率的变化。下图使用正弦函数编码，句子长度为50（纵坐标），编码向量维数128（横坐标），可以看到交替频率从左到右逐渐减慢。
那么在Transformer中这个位置编码向量是如何添加上的呢？通过Transformer的示例图可以看到，是将输入嵌入向量和位置编码向量相加，直接简单粗暴。也就是说，对于句子 $[w_1,\dots w_n]$ 中的每个词 $w_t$，计算输入模型的相应嵌入如下：
$${\psi }^{\prime }(w_t)=\psi (w_t)+\overrightarrow{p_t}$$
这里的$ \psi(w_t) $表示单词$w_t$的嵌入向量，$\vec{p_t}$表示单词$w_t$的位置编码向量。)同时为了使这种相加成为可能，需要保持位置嵌入的维度等于词嵌入的维度，即：
$$d_{\text{word embedding}}=d_{\text{positional embedding}}$$

相对性和绝对性

之前在面试的时候就遇到了这么一个问题。Transformer的位置编码是相对位置编码还是绝对位置编码？如果说是绝对问题编码，这个时候肯定会反问，Transformer的位置编码还有具备一定的相对性，能说一下其中的原理吗？这里其实就是个坑，因为已经有研究表明：在计算Attention之前，正弦位置编码的相对位置表达能力是存在的，当在计算Attention的时候需要通过$W^Q$、$W^K$、$W^V$投影矩阵变换来计算Q、K、V，这一步的投影矩阵变换就会破坏掉位置的相对性，所以又说Transformer的位置编码是绝对位置编码。

Transfomer位置编码的相对性

这里的主要原因是使用了正余弦位置编码，能让模型获取相对位置。以下是原文中的一段话：
We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $PEpos+k$ can be represented as a linear function of $P_{Epos}$.

那么为什么会成立呢？下面给出相关公式推导，比较简单。

Transformer位置编码又被称为三角式位置编码（Sinusoidal Position Embedding）；如下公式2所示，三角式位置编码通过在输入 $x_t,x_s$ 的嵌入维度上，依次加上不同频段的正余弦波位置编码：$p_t$、$p_s$。
$$A_{t,s}=q_t^T{k}_s=(x_t+p_t{)}^T{W}_Q^T{W}_K(x_s+p_s)$$
$$A_{t,s}=x_t^T{W}_Q^T{W}_K{x}_s+x_t^T{W}_Q^T{W}_K{p}_s+p_t^T{W}_Q^T{W}_K{x}_s+p_t^T{W}_Q^T{W}_K{p}_s(2)$$
$$p_t={\left[\cdots ,\sin \frac{t}{10000^{2n/d}},\cos \frac{t}{10000^{2n/d}},\cdots \right]}^T\in {\mathbb{R}}^d$$
意图在 $q_t,k_s$ 做内积时，得到若干余弦波的叠加，表示token间的相对位置信息，如公式3所示。
$$p_t^T{p}_s=\sum _{n=1}^{d/2}(\sin t{\theta }_n\sin s{\theta }_n+\cos t{\theta }_n\cos s{\theta }_n)=\sum _{n=1}^{d/2}\cos (t-s){\theta }_n(3)$$
$${\theta }_n=10000^{-2n/d}$$
通过上述公式可以看到，三角式位置编码可以让Transformer架构感知到序列的内在顺序与元素的相对位置。

Transfomer位置编码的绝对性

但事与愿违，由于计算Attention参数矩阵的存在，相对位置信息通过 $p_t^T{W}_Q^T{W}_K{p}_s$ （如公式2所示），而非 $p_t^T{p}_s$ 表示。如下图1所示，经过参数矩阵映射后的正余弦波乘积组合并不能表示为若干余弦波的组合，从而缺少单调性对应图1右图中黄色和绿色点线，其中蓝色点线表示理想情况，可以看到经过参数矩阵的映射，会导致Transformer架构无法真正地在计算自注意力矩阵时感知到元素的相对位置信息。

图1 经过参数矩阵映射过后，正余弦波乘积不再具有单调性，出自TENER论文

综上，Transformer 原版的位置编码，也就是正余弦函数位置编码，表达的是绝对位置信息，同时包含相对位置信息。但是经过线性变化，相对位置信息消失。基于此，需要对位置编码进行优化。

Transformer位置编码QA

为什么位置编码和词嵌入相加而不是拼接起来？

拿BERT的词嵌入由符号嵌入（Token Embedding）、片段嵌入（Segmentation Embedding）和位置嵌入（Position Embedding）直接相加得到，表示为
$$E_{word}=E_{tok}+E_{seg}+E_{pos}$$
上述三个嵌入分量都可以表达为“独热”（one-hot）编码表示输入与嵌入矩阵的乘积形式，即
$$E_{word}=O_{tok}{W}_{tok}^{|V|\times H}+O_{seg}{W}_{seg}^{|S|\times H}+O_{pos}{W}_{pos}^{|P|\times H}$$

其中，$O_{tok}$：依据符号在词典中位置下标、对输入符号构造的one-hot编码*表示；$O_{seg}$：依据符号在两个序列中隶属标签（更一般的为符号属性）下标、对输入符号构造的one-hot编码表示；$O_{pos}$：以符号在句子位置下标、对输入符号构造的one-hot编码表示；$W_{tok}^{|V|\times H}$、$W_{seg}^{|S|\times H}$和$W_{pos}^{|P|\times H}$分别为其对应的待训练嵌入参数矩阵；$|V|$、$|S|$和$|P|$分别为字典维度、序列个数（更一般的为符号属性）和最大位置数；$|H|$为嵌入维度。下面从三个角度理解合成：

角度1——从形象角度理解
上面的嵌入合成有点像在调颜色，先有一个基于字典的符号嵌入，“花里胡哨”的；然后按照符号类型属性（BERT为句子的隶属关系）添加颜色，相同的符号类型添加相同的颜色，于是具有相同属性符号的颜色就接近了一些；然后再按照位置，进一步添加不同的颜色。

角度2——从网络角度理解

（1）按照分别过网络再做求和融合的角度理解:三个one-hot编码向量与嵌入矩阵相乘，等价于构造三个以one-hot编码向量作为输入，输入维度分别为$|V|$、$|S|$和$|P|$，输出维度均为$H$的全连接网络。求和即为特征融合。如下图所示

（2）按照先做Concat融合再过网络的角度理解：三个one-hot编码向量与嵌入矩阵相乘，按照矩阵分块，可以改写为：
$$E_{word}=\left[\begin{array}{ccc}{O}_{tok}& O_{seg}& O_{pos}\end{array}\right]\left[\begin{array}{c}{W}_{tok}^{|V|\times H}\\ W_{seg}^{|S|\times H}\\ W_{pos}^{|P|\times H}\end{array}\right]$$
对应的全连接网络变为一个大网络，输入维度为$|V|+|S|+|P|$，输出维度还是$H$。对应的网络结构图形如下图所示：
角度3——从空间映射角度理解

三个嵌入的合成，是将符号空间、符号属性空间和位置空间三个看似“风马牛不相及”的空间表示，通过线性映射到一个统一的、同质的特征空间上去，然后再以求和的方式做坐标综合，如下图所示：

如果按照角度2的到底先融合还是后融合的两个视角，那上面说的是先映射后融合模式。当然，我们也可以按照角度2做先融合后映射的思考。先做如下铺垫：

类似于欧氏积空间（例如 ${\mathbb{R}}^3={\mathbb{R}}^2\times \mathbb{R}$）能够表达更高维的空间，人们也期望通过积（Product）的形式复合子流形的表达方式，将不同的流形复合，来刻画复杂的高维流形结构。定义如下形多个流形的笛卡尔积（Cartesian Product）

$$\mathcal{M}={\mathcal{M}}_1\times {\mathcal{M}}_2\times \cdots \times {\mathcal{M}}_c$$
其中，“$\times$”表示空间的笛卡尔积，${\mathcal{M}}_k(k=1,2,\dots ,c)$ 称为分量流形（Component Manifold）。设 ${\mathcal{M}}_k$ 为维度为 $n_k$ 的流形，则 $\mathcal{M}$ 也为一流形，称为积流形，其维度为 ${\sum }_{k=1}^c{n}_k$。证明从略。

对应上面铺垫和我们的问题，可以知道 $c=3$，${\mathcal{M}}_1$、${\mathcal{M}}_2$ 和 ${\mathcal{M}}_3$ 分别对应上面的符号空间、符号属性空间和位置空间。按照笛卡尔积的从“每个空间取点组团”的定义，我们的对三个one-hot编码的Concat操作即作出了 $|V|+|S|+|P|$ 维积流形中的一个点。然后再做的一个的线性映射，等于去获取该点的 $H$ 维内蕴坐标。

角度4——从最直观的角度来看

首先，如果我们回想一下上边的第一张可视化图，会发现位置编码向量的前几个维度用于存储关于位置的信息（注意，虽然示例中只有128维，但论文中的输入维度是512）。由于Transformer中的嵌入是从头开始训练的，所以设置参数的时候，可能不会把单词的语义存储在前几个维度中，这样就避开了位置编码。

虽然没有进行直接concat，但是进行了隐式concat。位置编码前半段比较有用，所以在编码嵌入向量的时候，将其语义信息往后放，下图可以帮你更好的理解：

所以对于这个问题，我认为最终的Transformer可以将单词的语义与其位置信息分开。此外，也没有理由支撑将二者分开拼接有什么好处，也许这样相加为模型提供比较好的特征。

另外，说到这里DeepSeek的位置编码就借鉴了这个思想：为了解决矩阵吸收无法添加位置编码的问题，DeepSeek将旋转位置编码和权重信息做了分割，最后在拼接到一块。具体的大家可以参考这篇文章：DeepSeek 注意力机制–MLA三连击（一）

Transformer有很多层，位置信息随着层数的对接，会消失吗？

Transformer架构配备了残差连接。因此，包含位置嵌入的模型输入信息可以有效地传播到更深层。如果不放心的话，可以在每一层都带上位置编码，比如2018 ICLR | Non-Autoregressive Neural Machine Translation，又比如Neural Machine Translation with Reordering Embeddings魔改每层都加一个新的Position encoding。

为什么同时使用正弦和余弦？

就我个人而言，我认为只有同时使用正弦和余弦，才能将$\sin (x+k)$和$\cos (x+k)$表示为$\sin (x)$和$\cos (x)$的线性变换。似乎你不能使用单个正弦或余弦做到同样的事情。另外一种思路是正余弦的交替在某种意义上等价于位置的二进制表示的alternating bits，也就是说类似于0、1交替；

为什么Transformer的正弦位置编码目前基本上都不用了？

正弦位置编码是一种绝对位置编码，并且可以方便的表达相对位置，看起来似乎挺完美。但为什么后来没人用了呢？答案是：正弦位置编码的相对位置表达能力被投影矩阵破坏掉了。具体解释可以详细看一下：本文的：Transformer位置编码的相对性和绝对性。

相对位置编码

与绝对位置编码只应用于输入层不同，相对位置编码在每一层中根据键和查询之间的偏移量进行计算，通常用于调整注意力分数，而不是直接与词元本身相加。这里看几种相对位置编码算法。

Transformer位置编码改进

既然相对位置信息是在计算Attention的时候丢失的，那么最直接的想法就是在计算Attention的时候再加回来。所以Transformer的原班人马，对此进行了改变，并提出了一种绝对位置编码（论文链接：https://arxiv.org/pdf/1803.02155）。具体做法是在计算attention score和weighted value时各加入一个可训练的表示相对位置的参数，并且multi head之间可以共享。

在正式进入讲解之前，先回顾一下self-attention。假设从多头注意力机制中的一个头输出后的序列是 $x=(x_1,...,x_n)$，其中$x_i\in {\mathbb{R}}^{d_x}$，这个时候，我们需要通过attention计算出一个新的序列 $z=(z_1,...,z_n)$，其中$z_i\in {\mathbb{R}}^{d_z}$。线性变换的输入元素的加权和计算公式如下：
$$z_i=\sum _{j=1}^n{a}_{ij}(x_j{W}^V)(1)$$
其中，权重系数 $a_{ij}$ 是通过softmax计算的：
$$a_{ij}=\frac{\exp (e_{ij})}{{\sum }_{k=1}^n\exp (e_{ik})}$$
使用兼容函数计算 $e_{ij}$，该函数比较两个输入元素（其中，使用Scaled dot product作为兼容函数计算是很高效的）：
$$e_{ij}=\frac{(x_i{W}^Q)(x_j{W}^K{)}^T}{\sqrt{d_z}}(2)$$
接下来说说Relation-aware自注意力，沿用上面的$x$的表示，将输入元素$x_i$和$x_j$之间的edge 表示为$a_{ij}^V,a_{ij}^K\in {\mathbb{R}}^{d_a}$，学习两个不同的edge表示的出发点是$a_{ij}^V$和$a_{ij}^K$适用于等式如下两个等式，这些表示可以在关注头之间共享，其中$d_a=d_z$。首先，修改等式(1)将edge信息传播到子层输出：
$$z_i=\sum _{j=1}^n{a}_{ij}(x_j{W}^V+a_{ij}^V)(3)$$
此扩展对于在任务中非常重要，其中任务由给定的注意头选择的edge类型信息对下游编码器或解码器层有用。同时，还修改了等式(2)确定兼容性时要考虑edge：
$$e_{ij}=\frac{(x_i{W}^Q)(x_j{W}^K+a_{ij}^K{)}^T}{\sqrt{d_z}}(4)$$
这里将edge信息通过简单加法合并进表示的主要原因是为了高效实现，这在后面会讲到。

对于线性序列，edge可以捕获有关输入元素之间相对位置差异的信息。我们考虑的最大相对位置被裁剪为最大绝对值$k$，因为假设精确的相对位置信息在一定距离之外没有用。剪裁最大距离还使模型能够泛化训练期间看不到的序列长度，因此，考虑$2k+1$个唯一的edge标签。
$$a_{ij}^K=w_{\text{clip}(j-i,k)}^K$$
$$a_{ij}^V=w_{\text{clip}(j-i,k)}^V$$
$$\text{clip}(x,k)=\max (-k,\min (k,x))$$
通过上式就可以学习相对位置的表示：
$w^K=(w_{-k}^K,...,w_k^K)$和$w^V=(w_{-k}^V,...,w_k^V)$
再优化一下，这里把等式(4)拆分开如下：
$$e_{ij}=\frac{x_i{W}^Q(x_j{W}^K)+x_i{W}^Q(a_{ij}^K{)}^T}{\sqrt{d_z}}(4)$$
然后我们就可以通过矩阵并行计算批量进入的数据了。

图1：表示相对位置或元素之间距离的示例边。我们在裁剪距离$k$内为每个相对位置学习表示。图中假设$2\le k\le n-4$。请注意，并非所有边都显示。

但最后作者表示：k>4以后效果就没有提升了，说明通常情况下，临域为4的窗口内(4 gram)，attention对相对位置比较敏感，窗口以外，相对位置可以不做区分。

Transformer-XL相对位置编码

为了方便介绍，这里对比了一下绝对位置编码和相对位置编码之间的区别和联系。此处以模型第一层计算为例，对使用绝对位置编码的注意力得分进行分解：
$$A_{ij}=x_i{W}^Q{W}^{K^T}{x}_j^T$$
$$=(v_i+p_i)W^Q{W}^{K^T}(v_j+p_j{)}^T$$
$$=v_i{W}^Q{W}^{K^T}{v}_j^T+v_i{W}^Q{W}^{K^T}{p}_j^T+p_i{W}^Q{W}^{K^T}{v}_j^T+p_i{W}^Q{W}^{K^T}{p}_j^T$$
与上述方法不同，Transformer-XL (论文链接：https://arxiv.org/pdf/1901.02860)提出了一种相对位置编码方法，在计算键和查询之间的注意力分数时引入了相对位置信息，具体公式如下：
$$A_{ij}=v_i{W}^Q{W}^{K^T}{v}_j^T+v_i{W}^Q{W}^{RT}{r}_{i-j}^T+f{W}^{K^T}{v}_j^T+g{W}^{RT}{r}_{i-j}^T$$
$$=v_i{W}^Q{W}^{K^T}{v}_j^T+v_i{W}^Q（r_{i-j}{W}^R{）}^T+f(v_j{W}^K{)}^T+g（r_{i-j}{W}^R{）}^T$$
其中，$r_{i-j}{W}^R$ 表示相对位置编码，$f$ 和 $g$ 是两个表示全局信息的参数。相比于绝对位置编码，注意力值的第二项和第四项对应的绝对位置编码 $p_j{W}^K$ 被替换为相对位置编码 $r_{i-j}{W}^R$，以引入相对位置信息；而第三和第四项中则使用全局参数 $f$ 和 $g$ 替换查询对应的绝对位置编码 $p_i{W}^Q$，分别用于衡量键和相对位置信息的重要程度。(注意：好像从这个工作开始，后续的RPE都只加到K上去，而不加到V上了。)

T5相对位置编码

作为另一种代表性方法，T5 提出了一种较为简化的相对位置编码TS Bias。具体来说，它在注意力分数中引入了可学习的标量，这些标量是基于查询和键的位置之间的距离进行计算的。与绝对位置编码相比，采用了相对位置编码的Transformer模型通常可以建模比训练序列更长的文本，即具备一定的长度外推能力（length extrapolation）。T5 相对位置编码的计算可以表达为：
$$A_{ij}=x_i{W}^Q{W}^{K^T}{x}_j^T+r_{i-j}$$
其中$r_{i-j}$表示基于查询和键之间偏移的可学习标量。注意：相对位置编码需要应用到Transformer的每一层，上面以及后面的$x_i$表示的是每一层的输入表示。

旋转位置编码(RoPE)

RoPE简单介绍

RoPE 代表了一种编码位置信息的新方法。传统方法中无论是绝对方法还是相对方法，都有其局限性。

• 绝对位置编码为每个位置分配一个唯一的向量，虽然简单但不能很好地扩展并且无法有效捕获相对位置；

• 相对位置编码关注Token之间的距离，增强模型对Token关系的理解，但使模型架构复杂化。

RoPE巧妙地结合了两者的优点。允许模型理解标记的绝对位置及其相对距离的方式对位置信息进行编码。这是通过旋转机制实现的，其中序列中的每个位置都由嵌入空间中的旋转表示。RoPE 的优雅之处在于其简单性和高效性，这使得模型能够更好地掌握语言语法和语义的细微差别。

RoPE原理介绍

其实旋转位置编码最关键的就是旋转矩阵，分别对Q、K做旋转位置编码，然后计算注意力。先看一下旋转矩阵如下：
$$R_{\theta ,i}=\left[\begin{array}{ccccccc}\cos t{\theta }_1& -\sin t{\theta }_1& 0& 0& \cdots & 0& 0\\ \sin t{\theta }_1& \cos t{\theta }_1& 0& 0& \cdots & 0& 0\\ 0& 0& \cos t{\theta }_2& -\sin t{\theta }_2& \cdots & 0& 0\\ 0& 0& \sin t{\theta }_2& \cos t{\theta }_2& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & \cos t{\theta }_{H/2}& -\sin t{\theta }_{H/2}\\ 0& 0& 0& 0& \cdots & \sin t{\theta }_{H/2}& \cos t{\theta }_{H/2}\end{array}\right]$$
旋转矩阵源自我们在高中学到的正弦和余弦的三角性质，使用二维矩阵应该足以获得旋转矩阵的理论，先看一下它经典的图：

根据三角函数的特性，索引为$i$的旋转矩阵和索引为$j$的旋转矩阵转置的乘积等同于索引为相对距离$i-j$的旋转矩阵，即$R_{\theta ,i}{R}_{\theta ,j}^T=R_{\theta ,i-j}$（看了很多文章，公式比较复杂目的就是为了证明这个）。通过这种方式，能够将相对位置信息融入注意力分数，其计算公式如下：
$$q_i=x_i{W}^Q{R}_{\theta ,i},k_j=x_j{W}^K{R}_{\theta ,j}$$
$$A_{ij}=(x_i{W}^Q{R}_{\theta ,i})(x_j{W}^K{R}_{\theta ,j}{)}^T=x_i{W}^Q{R}_{\theta ,i-j}{W}^{K^T}{x}_j^T$$
根据旋转矩阵的定义，RoPE在处理查询和键向量时，将连续出现的两个元素视为一个子空间（subspace）。因此，对于一个长度为$H$的向量来说，将会形成$H/2$个子空间。在这些子空间中，每一个子空间 i ∈ { 1 , ⋯   , H / 2 } i \in \{1, \cdots, H/2\} i∈{1,⋯,H/2}所对应的两个元素都会根据一个特定的旋转角度$t\cdot {\theta }_i$进行旋转，其中$t$代表位置索引，而${\theta }_i$表示该子空间中的旋转基。与正弦位置编码类似[12]，RoPE将旋转基${\theta }_i$定义为底数$b$（默认值是10000）的指数：
Θ = { θ i = b − 2 ( i − 1 ) / H ∣ i ∈ { 1 , 2 , ⋯   , H / 2 } } \Theta = \{\theta_i = b^{-2(i-1)/H} | i \in \{1, 2, \cdots, H/2\}\} \quad Θ={θi​=b−2(i−1)/H∣i∈{1,2,⋯,H/2}}
其中：当b=10000的时候，${\theta }_i$写成下面的表示方式更好理解一些：
$${\theta }_i=\frac{1}{10000^{2\ast (i-1)/H}}$$
这里在回头看一下对应的旋转矩阵$R_{\theta ,i}$，因为这个矩阵比较稀疏，很多都是0，会造成计算上的浪费，所以在计算时采用逐位相乘再相加的方式进行，相关计算方式如下：
$$\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\\ ⋮\\ q_{d-2}\\ q_{d-1}\end{array}\right]\otimes \left[\begin{array}{c}\cos m{\theta }_1\\ \cos m{\theta }_1\\ \cos m{\theta }_2\\ \cos m{\theta }_2\\ ⋮\\ \cos m{\theta }_{H/2}\\ \cos m{\theta }_{H/2}\end{array}\right]+\left[\begin{array}{c}-q_1\\ q_0\\ -q_3\\ q_2\\ ⋮\\ -q_{d-1}\\ q_{d-2}\end{array}\right]\otimes \left[\begin{array}{c}\sin m{\theta }_1\\ \sin m{\theta }_1\\ \sin m{\theta }_2\\ \sin m{\theta }_2\\ ⋮\\ \sin m{\theta }_{H/2}\\ \sin m{\theta }_{H/2}\end{array}\right]$$

这里$q$代表的就是K或者Q的一个行向量中的某个元素，这里的$\otimes$表示的矩阵逐位相乘。

RoPE应用实例

如果前面的公式没有看懂，这里为了方便理解，举个实际应用案例，再把旋转位置编码原理图放在这里：

再看这个图或许你还有点懵，下面一点点的带你理解一下，假设“我”、“来自”、“美丽”、“的”Q、K向量表示为如下，其中每行向量代表一个Token：

$$Q=\left[\begin{array}{ccccccccc}& -1.1258& -1.1524& -0.2506& -0.4339& 0.8487& 0.6920& -0.3160& -2.1152\\ & 0.3223& -1.2633& 0.3500& 0.3081& 0.1198& 1.2377& 1.1168& -0.2473\\ & -1.3527& -1.6959& 0.5667& 0.7935& 0.5988& -1.5551& -0.3414& 1.8530\\ & 0.7502& -0.5855& -0.1734& 0.1835& 1.3894& 1.5863& 0.9463& -0.8437\end{array}\right]$$

$$K=\left[\begin{array}{ccccccccc}& -0.6136& 0.0316& -0.4927& 0.2484& 0.4397& 0.1124& 0.6408& 0.4412\\ & -0.1023& 0.7924& -0.2897& 0.0525& 0.5229& 2.3022& -1.4689& -1.5867\\ & -0.6731& 0.8728& 1.0554& 0.1778& -0.2303& -0.3918& 0.5433& -0.3952\\ & -0.4462& 0.7440& 1.5210& 3.4105& -1.5312& -1.2341& 1.8197& -0.5515\end{array}\right]$$
原理图中的绿色部分想要表达的就是下图的这个意思：两两划分：
根据$Q、K$的维度信息，然后找到上述公式中的位置索引 $t$ 矩阵（这里是横向的），如下所示：
$$t=\left[\begin{array}{ccccccccc}& 0& 1& 2& 3& 4& 5& 6& 7\end{array}\right]$$
然后计算出对应的 $\Theta$，其中包含的是每个 ${\theta }_i$：
$$\Theta =\left[\begin{array}{ccccc}& \frac{1}{10000^{2\ast (1-1)/8}}& \frac{1}{10000^{2\ast (2-1)/8}}& \frac{1}{10000^{2\ast (3-1)/8}}& \frac{1}{10000^{2\ast (4-1)/8}}\end{array}\right]$$
上面的$i$的取值为：$i\in 1,2,\cdots ,H/2$ （这里的H=8，因为向量维度为8）。现在有了$\Theta$就可以计算旋转矩阵$R_{\theta ,i}$了，此时Q向量矩阵第一行对应的旋转矩阵为：
$$\left[\begin{array}{ccccccccc}& \cos (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& -\sin (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& 0& 0& 0& 0& 0& 0\\ & \sin (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& \cos (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& 0& 0& 0& 0& 0& 0\\ & 0& 0& \cos (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& -\sin (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& 0& 0& 0& 0\\ & 0& 0& \sin (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& \cos (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& 0& 0& 0& 0\\ & 0& 0& 0& 0& \cos (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& -\sin (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& 0& 0\\ & 0& 0& 0& 0& \sin (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& \cos (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& 0& 0\\ & 0& 0& 0& 0& 0& 0& \cos (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& -\sin (\frac{0\times 1}{10000^{2\ast (1-1)/8}})\\ & 0& 0& 0& 0& 0& 0& \sin (\frac{0\times 1}{10000^{2\ast (1-1)/8}})& \cos (\frac{0\times 1}{10000^{2\ast (1-1)/8}})\end{array}\right]$$
此时就可以计算出Q旋转后的矩阵了，同理，也可以计算出K旋转后的矩阵，之后就可以采用Attention计算公式来计算Attention分数了。

RoPE代码理解

这个函数将相对位置编码（RoPE）应用到注意力机制中的查询和键上。这样，模型就可以根据相对位置关注不同的位置

import torch
import torch.nn as nn
import torch.nn.functional as F
import math
 
 
def RoPE(q, k):
    # q,k: (bs, head, max_len, output_dim)
    batch_size = q.shape[0]
    nums_head = q.shape[1]
    max_len = q.shape[2]
    output_dim = q.shape[-1]
 
    # (bs, head, max_len, output_dim)
    pos_emb = sinusoidal_position_embedding(batch_size, nums_head, max_len, output_dim, q.device)
 
 
    # cos_pos,sin_pos: (bs, head, max_len, output_dim)
    # 看rope公式可知，相邻cos，sin之间是相同的，所以复制一遍。如(1,2,3)变成(1,1,2,2,3,3)
    cos_pos = pos_emb[...,  1::2].repeat_interleave(2, dim=-1)  # 将奇数列信息抽取出来也就是cos 拿出来并复制
    sin_pos = pos_emb[..., ::2].repeat_interleave(2, dim=-1)  # 将偶数列信息抽取出来也就是sin 拿出来并复制
 
    # q,k: (bs, head, max_len, output_dim)
    q2 = torch.stack([-q[..., 1::2], q[..., ::2]], dim=-1)
    q2 = q2.reshape(q.shape)  # reshape后就是正负交替了
 
    # 更新qw, *对应位置相乘
    q = q * cos_pos + q2 * sin_pos
 
    k2 = torch.stack([-k[..., 1::2], k[..., ::2]], dim=-1)
    k2 = k2.reshape(k.shape)
    # 更新kw, *对应位置相乘
    k = k * cos_pos + k2 * sin_pos
 
    return q, k

其中：sinusoidal_position_embedding代码如下，这个函数用来生成正弦形状的位置编码。这种编码用来在序列中的令牌中添加关于相对或绝对位置的信息

def sinusoidal_position_embedding(batch_size, nums_head, max_len, output_dim, device):
    # (max_len, 1)
    position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(-1)
 
    # (output_dim//2)
    # 即公式里的i, i的范围是 [0,d/2]
    ids = torch.arange(0, output_dim // 2, dtype=torch.float)  
    theta = torch.pow(10000, -2 * ids / output_dim)
 
    # (max_len, output_dim//2)
    # 即公式里的：pos / (10000^(2i/d))
    embeddings = position * theta 
 
    # (max_len, output_dim//2, 2)
    embeddings = torch.stack([torch.sin(embeddings), torch.cos(embeddings)], dim=-1)
 
    # (bs, head, max_len, output_dim//2, 2)
    # 在bs维度重复，其他维度都是1不重复
    embeddings = embeddings.repeat((batch_size, nums_head, *([1] * len(embeddings.shape))))  
 
    # (bs, head, max_len, output_dim)
    # reshape后就是：偶数sin, 奇数cos了
    embeddings = torch.reshape(embeddings, (batch_size, nums_head, max_len, output_dim))
    embeddings = embeddings.to(device)
    return embeddings

为一目了然起见，还是一步一步通过一个示例来加深理解

sinusoidal_position_embedding函数生成位置嵌入。但为了简单起见，我们只考虑前8个维度，前4个维度为sin编码，后4个维度为cos编码。所以，我们可能得到类似以下的位置嵌入

# 注意，这只是一个简化的例子，真实的位置嵌入的值会有所不同。
pos_emb = torch.tensor([[[
                   [0.0000, 0.8415, 0.9093, 0.1411, 1.0000, 0.5403, -0.4161, -0.9900],
                   [0.8415, 0.5403, 0.1411, -0.7568, 0.5403, -0.8415, -0.9900, -0.6536],
                   [0.9093, -0.4161, -0.8415, -0.9589, -0.4161, -0.9093, -0.6536, 0.2836]
                   ]]])

然后，我们提取出所有的sin位置编码和cos位置编码，并在最后一个维度上每个位置编码进行复制

sin_pos = pos_emb[..., ::2].repeat_interleave(2, dim=-1)  # 提取出所有sin编码，并在最后一个维度上复制
cos_pos = pos_emb[..., 1::2].repeat_interleave(2, dim=-1)  # 提取出所有cos编码，并在最后一个维度上复制

更新query向量：我们首先构建一个新的q2向量，这个向量是由原来向量的负的cos部分和sin部分交替拼接而成的，我们用cos_pos对q进行元素级乘法，用sin_pos对q2进行元素级乘法，并将两者相加得到新的query向量

q2 = torch.stack([-q[..., 1::2], q[..., ::2]], dim=-1).flatten(start_dim=-2)
# q2: tensor([[[[-0.2,  0.1, -0.4,  0.3, -0.6,  0.5, -0.8,  0.7],
#               [-1.0,  0.9, -1.2,  1.1, -1.4,  1.3, -1.6,  1.5],
#               [-1.8,  1.7, -2.0,  1.9, -2.2,  2.1, -2.4,  2.3]]]])
 
q = q * cos_pos + q2 * sin_pos

公式表示如下：
$$\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\\ ⋮\\ q_{d-2}\\ q_{d-1}\end{array}\right]\otimes \left[\begin{array}{c}\cos m{\theta }_1\\ \cos m{\theta }_1\\ \cos m{\theta }_2\\ \cos m{\theta }_2\\ ⋮\\ \cos m{\theta }_{H/2}\\ \cos m{\theta }_{H/2}\end{array}\right]+\left[\begin{array}{c}-q_1\\ q_0\\ -q_3\\ q_2\\ ⋮\\ -q_{d-1}\\ q_{d-2}\end{array}\right]\otimes \left[\begin{array}{c}\sin m{\theta }_1\\ \sin m{\theta }_1\\ \sin m{\theta }_2\\ \sin m{\theta }_2\\ ⋮\\ \sin m{\theta }_{H/2}\\ \sin m{\theta }_{H/2}\end{array}\right]$$
更新key向量：对于key向量，我们的处理方法与query向量类似：

k2 = torch.stack([-k[..., 1::2], k[..., ::2]], dim=-1).flatten(start_dim=-2)
# k2: tensor([[[[-0.15,  0.05, -0.35,  0.25, -0.55,  0.45, -0.75,  0.65

ALiBi位置编码

ALiBi简单介绍

ALiBi全称是线性偏差注意力方法（Attention with Linear Biases），最早于2021年在ICLR2022国际顶会上发表。论文链接：TRAIN SHORT, TEST LONG: ATTENTION WITH LINEAR BIASES ENABLES INPUT LENGTH EXTRAPOLATION。

它是一种特殊的相对位置编码，主要用来增强Transformer模型的长度外推能力。它既不像Transformer的正弦位置编码将编码向量与输入嵌入向量直接相加，也不像RoFE旋转位置编码一样，对Q、K矩阵做旋转位置变换，而是在原始的注意力计算公式上，进一步引入了与相对距离成正比例关系的惩罚因子来调整注意力分数。

ALiBi原理介绍

具体来说，ALiBi位置编码在原始的注意力计算公式上，进一步引入了与相对距离成比例关系的惩罚因子来调整注意力分数：
$$A_{ij}=x_i{W}^Q{W}^{K^T}{x}_j^T-m(i-j)$$
其中，$i-j$ 是查询和键之间的位置偏移量，$m$ 是每个注意力头独有的惩罚系数。ALiBi 中的惩罚分数是预先设定的，无须引入额外的训练参数。下面是ALiBi位置编码的示意图。

首先，我们看一下前面两个矩阵是怎么个事情：当计算每个头的注意力分数时，会向每个注意力分数($q_i,k_i$)添加一个常数偏差。左边是自注意力得分，关于q和k的内积，右边是一个相对距离的矩阵。这里假设$Q=[q_1,q_2,q_3,q_4,q_5]$、$K=[k_1,k_2,k_3,k_4,k_5]$，对照上图可以看到：

• $q_1$和$k_1$之间的距离是0，所以对应位置就是0
• $q_2$和$k_1$之间的距离是：（k的索引）-（q的索引），即：1-2 = -1，就对应到了右侧矩阵的值为-1；
• 以此类推，相对距离矩阵的中间对角线上都是0，然后左下角的取值都是对应的（k的索引）-（q的索引）；

然后，我们再看一下m取值是怎么个事情，按论文中的说法是

• 当8个头（heads）的时候，$m$的取值为：
  $$\frac{1}{2^1},\frac{1}{2^2},\cdots ,\frac{1}{2^8},1,2,...,i$$

• 如果是16个头，则$m$的取值为：
  $$\frac{1}{2^{0.5}},\frac{1}{2^1},\frac{1}{2^{1.5}},\cdots ,\frac{1}{2^8}$$
  相当于追加了一半的$1/\sqrt{(}2)$到原来的8个头的每个$m$的取值

• 扩展到一般情况就是：对于$n$个头的话，$m$的取值就是$2^{-\frac{8}{n}}$，即如下
  $$2^{-\frac{8}{1}},2^{-\frac{8}{2}},2^{-\frac{8}{3}},...,2^{-\frac{8}{n}}$$

最后，ALiBi位置编码的Attention注意力分数计算如下：
$$\text{softmax}({\mathbf{q}}_i{\mathbf{K}}^{\top }+m\cdot [-(i-1),\dots ,-2,-1,0])$$

对于第$i$个query来说，他们之间的相对距离就是：$k$的索引 - $q$的索引，具体而言，$k$的索引遍历$1,2,\dots ,i$，而$q$的索引取值为$i$。

可以看到，ALiBi不需要任何额外的参数，所以通过这种方式不会增加模型的复杂性。BLOOM模型架构就是采用的ALiBi的位置编码方法。

ALiBi代码示例

import torch
import torch.nn as nn
import torch.nn.functional as F

class ALiBi(nn.Module):
    def __init__(self, num_heads, max_seq_len):
        super(ALiBi, self).__init__()
        self.num_heads = num_heads
        self.max_seq_len = max_seq_len
        self.slopes = torch.tensor([2 ** (-8 + i * 8 / (num_heads - 1)) for i in range(num_heads)])
        self.biases = self._create_biases()

    def _create_biases(self):
        # 创建位置偏置矩阵
        biases = torch.zeros((self.num_heads, self.max_seq_len, self.max_seq_len))
        for head in range(self.num_heads):
            for i in range(self.max_seq_len):
                for j in range(self.max_seq_len):
                    biases[head, i, j] = self.slopes[head] * (i - j)
        return biases

    def forward(self, q, k):
        # q: (batch_size, seq_len, num_heads, head_dim)
        # k: (batch_size, seq_len, num_heads, head_dim)
        seq_len = q.size(1)
        biases = self.biases[:, :seq_len, :seq_len].to(q.device)
        attention_scores = torch.einsum("bqhd,bkhd->bhqk", q, k) + biases
        return attention_scores

# 示例使用
if __name__ == "__main__":
    num_heads = 8
    max_seq_len = 10
    head_dim = 64
    batch_size = 2

    # 创建ALiBi位置编码模块
    alibi = ALiBi(num_heads, max_seq_len)

    # 创建随机的查询和键
    q = torch.randn(batch_size, max_seq_len, num_heads, head_dim)
    k = torch.randn(batch_size, max_seq_len, num_heads, head_dim)

    # 计算注意力分数
    attention_scores = alibi(q, k)
    print("Attention Scores Shape:", attention_scores.shape)
    print("Attention Scores:", attention_scores)

DeepSeek位置编码

位置编码简单介绍

在聊DeepSeek位置编码之前，这里稍微总结一下。最原始的Transformer采用的是正弦位置编码，根据正余弦位置函数来生成位置编码向量，将其添加到输入嵌入向量上面，可以理解为在计算Attention之前添加位置信息；

Transformer正余弦位置编码尽管是在输入向量中引了相对信息，但在计算Attention Q、K矩阵的时候会导致相对信息丢失，所以后面就有了相对位置编码，相对位置位置编码主要面向的就是Q、K矩阵，这个比较有代表性的就是Transformer-XL位置编码、T5位置编码、RoPE位置编码、ALiBi位置编码等，它们都是在计算Attention过程中对Q、K增加位置信息，然后再计算Attention分数。

尽管经过最近几年的发展出现了很多的相对位置编码算法，但是当前主流大模型架构采用最多的其实就是RoFE位置编码，即使DeepSeek也不例外，但是DeepSeek从工程化的角度对其做了优化。

简单来说，DeepSeek的创新点主要有三部分：低秩信息压缩、矩阵吸收、位置编码改进。具体得大家可以参考这两篇文章：DeepSeek 注意力机制–MLA三连击（二）；这一节主要介绍DeepSeek的位置编码部分。

位置编码原理

前面介绍了RoFE位置编码，即在计算注意力之前前，代码是先应用参数权重矩阵$W^Q$、 $W^K$ 得到$Q$和$K$，然后在$Q$和$K$上施加RoPE（乘以一个旋转矩阵），来融入相对位置信息。

但是由于DeepSeek做了低秩转换，此时的K和V的低秩表示已经是压缩了的状态，压缩操作可能已经丢失了某些信息，而RoPE矩阵对key和value是位置敏感的，直接在 $c_t^Q$ 和 $c_t^{KV}$ 上应用$R_m$和$R_n$ 不再等价于在完整的Q和K上应用位置编码，不能直接和有效地反映原始Q和K的相对位置关系。

换言之，RoPE与低秩KV压缩不兼容（RoPE is incompatible with low-rank KV compression），只能作用到原始K和V上。即只能从低秩KV压缩先还原成原始的KV，然后在原始KV上施加RoPE。这样会影响模型性能，所以作者采用了权重吸收，然而却不能兼容RoFE。

为此，DeepSeek提出了解耦RoPE的策略，对Q、K做两部分的拆分，一部分用来表示旋转位置编码（低维度），另外一部分表示文本嵌入（高维度），最后将两部分合并到一块来实现相对位置信息的添加；如下图：前面的高维度向量称为nope，后面的低维度向量称为rope。

具体而言是，把Query和Key进行拆分为$[q_t^R,q_t^C]$和$[k_t^R,k_t^C]$，其中一部分小向量进行了旋转位置编码（$q_t^R,k_t^R$），一部分大向量进行压缩（$q_t^C,k_t^C$）。

• 信息存储部分（$q_t^C,k_t^C$）。这部分存储了大部分的业务信息，是被压缩的。下图的红圈和紫圈表明，我们有$n_h$个注意力头，因此，我们需要把$q_t^C,k_t^C$分别均分为$n_h$份。下标i表示的是第i个头。
• 位置信息部分（$q_t^R,k_t^R$）。具体又分为两部分：
• 使用共享的键（shared keys）$k_t^R\in {\mathbb{R}}^{d_h^R}$来携带RoPE信息，$d_h^R$表示解耦的queries和key的一个head的维度。共享的$k_t^R$指的是每个头的K都用这同一个$k_t^R$。注意，此处是基于$h_t$（输入嵌入）而不是基于向下投影的$C_t^{KV}$来生成$k_t^R$。
• 使用额外的多头查询（multi-head queries）$q_{t,i}^R\in {\mathbb{R}}^{d_h^R}$来携带RoPE位置信息。注意，此处是基于$c_t^Q$生成$q_{t,i}^R$，而且每个头会有自己的$q_{t,i}^R$。

最后将这四个变量分别拼接起来进行注意力计算。从而在推理时不需要对Key进行位置编码的计算，避免了RoPE与低秩压缩矩阵之间的耦合问题，解决了位置信息与推理效率之间的矛盾，提高了推理效率。具体参见下图。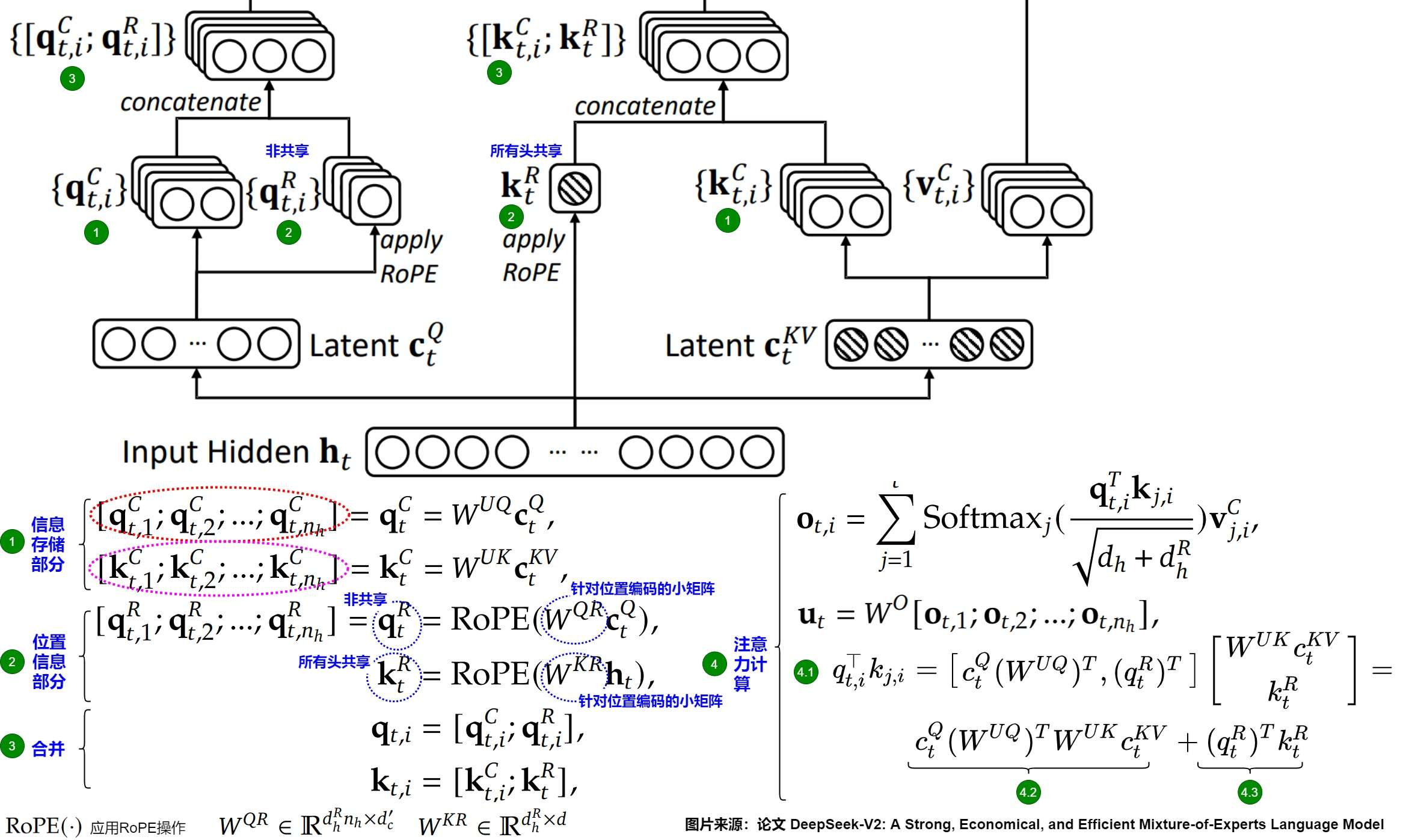

最终乘积计算如图中标号4.1，其中前一项（标号4.2）按照无RoPE的情况计算，推理时只需要缓存$c_t^{KV}$，后者（标号4.3）则对于所有注意力头只缓存一个共享$k_t^R$。即，在推理阶段，单个Token产生的KV Cache包含了两个部分。

• 需要缓存键值的压缩潜在向量$c_t^{KV}$（维度为$d_c$）。
• 携带RoPE信息的共享键向量$k_t^R$（维度为$d_h^R$）。

一共是$(d_c+d_h^R)l$个元素，l是层数。这种折中的方法保证了KV Cache的显存空间依然很小（虽然在$d_c$的基础上增加了64维的$d_h^R$），FLOPS上有增加但是代价不大。

经过Concat过程会增加Q和K向量的维度。为了处理增加的维度，模型可以选择:

• 增加注意力头的数量：这将保持原有的每头维度，但需要更多的计算资源。
• 调整每个头的处理维度：保持头的数量不变，但提高每个头的维度，以适应Concat向量。

下图给出了清晰的对比。进行注意力计算时，$c_t^{KV}$分别通过上投影矩阵$W^{UK}$和$W^{UV}$还原出键和值，每个注意力头上的键再与携带了RoPE信息的共享键向量$k_t^R$拼接形成MHA的键值输入。

$c_t^Q$通过上投影矩阵$W^{UQ}$和$W^{UR}$还原并生成查询向量$q_t^C$和携带RoPE信息的查询向量$q_t^R$，二者拼接形成MHA的查询向量输入。最终多个头的输入拼接在一起，并经过线性映射$W^O$得到最终的输出。

代码示例

下面是前向传播的代码，更加详细的代码介绍可以参考这篇文章：DeepSeek 注意力机制–MLA三连击（三）

def forward(
    self,
    hidden_states: torch.Tensor, # 输入的隐藏状态，形状为 (batch_size, seq_length, hidden_size)
    attention_mask: Optional[torch.Tensor] = None, #用于屏蔽某些位置的注意力计算
    position_ids: Optional[torch.LongTensor] = None, #用于旋转位置编码
    past_key_value: Optional[Cache] = None, #可选的缓存，用于加速推理。V2代码中，kv cache存储的是全部缓存，不是压缩后的
    output_attentions: bool = False, # 是否返回注意力权重
    use_cache: bool = False, #是否使用缓存
    **kwargs,
) -> Tuple[torch.Tensor, Optional[torch.Tensor], Optional[Tuple[torch.Tensor]]]:

    # hidden_states对应公式中的h_t，的shape是(batch_size, seq_length,hidden_size)
    bsz, q_len, _ = hidden_states.size()
    
    # query向量计算，先后两次映射，中间加一次归一化
    q = self.q_b_proj(self.q_a_layernorm(self.q_a_proj(hidden_states)))
    q = q.view(bsz, q_len, self.num_heads, self.q_head_dim).transpose(1, 2)
    
    #query向量做分割，一部分做旋转位编码，一部分是嵌入信息
    q_nope, q_pe = torch.split(
        q, [self.qk_nope_head_dim, self.qk_rope_head_dim], dim=-1
    )
    
   # 将输入的隐藏状态投影到压缩的键和值空间。
    compressed_kv = self.kv_a_proj_with_mqa(hidden_states)
    
    # 将压缩后的键和值向量分为两部分
    compressed_kv, k_pe = torch.split(
        compressed_kv, [self.kv_lora_rank, self.qk_rope_head_dim], dim=-1
    )
    k_pe = k_pe.view(bsz, q_len, 1, self.qk_rope_head_dim).transpose(1, 2)
    
    # 将压缩后的键和值向量进一步投影
    kv = (
        self.kv_b_proj(self.kv_a_layernorm(compressed_kv))
        .view(bsz, q_len, self.num_heads, self.qk_nope_head_dim + self.v_head_dim)
        .transpose(1, 2)
    )
    # 将键和值向量分为两部分
    k_nope, value_states = torch.split(
        kv, [self.qk_nope_head_dim, self.v_head_dim], dim=-1
    )
    kv_seq_len = value_states.shape[-2]
    
    #如果使用缓存，更新键和值向量的序列长度，考虑缓存中的内容。
    if past_key_value is not None:
        kv_seq_len += past_key_value.get_usable_length(kv_seq_len, self.layer_idx)
    
    #计算旋转位置编码所需的余弦和正弦值。
    cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len)
    #将旋转位置编码应用于查询向量和键向量。
    q_pe, k_pe = apply_rotary_pos_emb(q_pe, k_pe, cos, sin, position_ids)
    
    # 将不使用旋转位置编码的部分和使用旋转位置编码的部分组合起来
    query_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)
    query_states[:, :, :, : self.qk_nope_head_dim] = q_nope
    query_states[:, :, :, self.qk_nope_head_dim :] = q_pe

    key_states = k_pe.new_empty(bsz, self.num_heads, q_len, self.q_head_dim)
    key_states[:, :, :, : self.qk_nope_head_dim] = k_nope
    key_states[:, :, :, self.qk_nope_head_dim :] = k_pe
    
    # 如果使用缓存，更新键和值向量，将当前的键和值向量与缓存中的内容合并
    if past_key_value is not None:
        cache_kwargs = {"sin": sin, "cos": cos}  # Specific to RoPE models
        key_states, value_states = past_key_value.update(
            key_states, value_states, self.layer_idx, cache_kwargs
        )
    
    # 计算查询向量和键向量的点积，得到注意力分数
    attn_weights = (
        torch.matmul(query_states, key_states.transpose(2, 3)) * self.softmax_scale
    )
    
    # 提供了注意力掩码，将其添加到注意力分数中，以屏蔽某些位置的注意力
    if attention_mask is not None:
        attn_weights = attn_weights + attention_mask

    # 使用 softmax 函数对注意力分数进行归一化
    attn_weights = nn.functional.softmax(
        attn_weights, dim=-1, dtype=torch.float32
    ).to(query_states.dtype)
    
    # 对注意力权重应用 dropout，以防止过拟合
    attn_weights = nn.functional.dropout(
        attn_weights, p=self.attention_dropout, training=self.training
    )
    
    # 使用注意力权重对值向量进行加权求和，得到最终的输出
    attn_output = torch.matmul(attn_weights, value_states)
    attn_output = attn_output.transpose(1, 2).contiguous()
    attn_output = attn_output.reshape(bsz, q_len, self.num_heads * self.v_head_dim)
    attn_output = self.o_proj(attn_output)

    if not output_attentions:
        attn_weights = None

    return attn_output, attn_weights, past_key_value

实际计算流程图如下所示：

推荐阅读

[1] Transformer|详细了解前馈神经网络（FFN）

[2] Transformer|从MHA到DeepSeek MLA，非常详细！

[3] Transformer|一文了解注意力机制（Attention）

[4] Transformer|大模型MoE架构（含DeepSeek MoE详解）

[5] Transformer|一文了解归一化(Normalization)

AI-Agent文章推荐

[1]盘点一下！大模型Agent“花式玩法”

[2]2025年的风口！| 万字长文纵观大模型Agent！

[3]大模型Agent的 “USB”接口！| 一文详细了解MCP（模型上下文协议）

[4]2025年的风口！| 万字长文纵观大模型Agent！

[5]万字长文！从AI Agent到Agent工作流，一文详细了解代理工作流(Agentic Workflows)

更多精彩内容–>专注大模型/AIGC、Agent、RAG等学术前沿分享！