探秘Transformer系列之（29）--- DeepSeek MoE

从零开始解析Transformer，目标是：(1) 解析Transformer如何运作，以及为何如此运作，让新同学可以入门；(2) 力争融入一些比较新的或者有特色的论文或者理念，让老鸟也可以有所收获。

罗西的思考

715人浏览 · 2025-04-20 10:10:56

罗西的思考 · 2025-04-20 10:10:56 发布

探秘Transformer系列之（29）— DeepSeek MoE

文章目录

探秘Transformer系列之（29）--- DeepSeek MoE

0x00 概述

MoE有两个鲜明特点：

动态路由：使用门控网络（Gating Network）来决定每个输入应由哪些专家处理。
稀疏激活：对于每个输入,只有部分专家被激活，大大减少了计算量。

也正是由于这两个特点导致了几大难题：

负载均衡。某些专家的过度使用导致负载分布不均。
路由网络退化。由于门控网络路由决策的过拟合，探索能力下降。
参数爆炸。专家数量增加导致过高的内存和存储需求。
通信瓶颈。在分布式系统中，专家之间的高通信开销尤其突出。
内存碎片化。不高效的内存使用导致训练期间出现内存不足错误。
在模型精度（trim token）和硬件效能（zero padding）之间如何平衡（Tradeoff ）。

这些难题中，又以负载均衡最为典型，我们接下来进行深入分析，看看业界如何应对负载均衡问题。

注：

全部文章列表在这里，估计最终在35篇左右，后续每发一篇文章，会修改此文章列表。探秘Transformer系列之文章列表
本系列是对论文、博客和代码的学习和解读，借鉴了很多网上朋友的文章，在此表示感谢，并且会在参考中列出。因为本系列参考文章太多，可能有漏给出处的现象。如果原作者或者其他朋友发现，还请指出，我在参考文献中进行增补。

探秘Transformer系列之（1）：注意力机制

探秘Transformer系列之（2）—总体架构

探秘Transformer系列之（3）—数据处理

探秘Transformer系列之（4）— 编码器 & 解码器

探秘Transformer系列之（5）— 训练&推理

探秘Transformer系列之（6）— token

探秘Transformer系列之（7）— embedding

探秘Transformer系列之（8）— 位置编码

探秘Transformer系列之（9）— 位置编码分类

探秘Transformer系列之（10）— 自注意力

探秘Transformer系列之（11）— 掩码

探秘Transformer系列之（12）— 多头自注意力

探秘Transformer系列之（13）— FFN

探秘Transformer系列之（14）— 残差网络和归一化

探秘Transformer系列之（15）— 采样和输出

探秘Transformer系列之（16）— 资源占用)

探秘Transformer系列之（17）— RoPE（上）

探秘Transformer系列之（17）— RoPE（下）

探秘Transformer系列之（18）— FlashAttention

探秘Transformer系列之（19）----FlashAttention V2 及升级版本

探秘Transformer系列之（20）— KV Cache

探秘Transformer系列之（21）— MoE

探秘Transformer系列之（22）— LoRA

探秘Transformer系列之（23）— 长度外推

探秘Transformer系列之（24）— KV Cache优化

探秘Transformer系列之（25）— KV Cache优化之处理长文本序列

探秘Transformer系列之（26）— KV Cache优化之 PD分离or合并

探秘Transformer系列之（27）— MQA & GQA

探秘Transformer系列之（28）— DeepSeek MLA（上）

探秘Transformer系列之（28）— DeepSeek MLA（下）

0x01 难点

我们先给出一个例子来进行说明。

我们需要开发应用，但是此应用需要有前台开发和后台开发，那么招聘程序员有两种选择：

雇佣一位同时精通前台开发和后台开发的程序员，这样他可以完成所有开发。这类似于标准 Transformer 模型，由单个 FFN 子层处理所有输入 token。
雇佣多位各有所长的程序员，比如前台开发程序员和后台开发程序员，再加上一位开发经理来分配工作。这类似于 MoE 方法，每个程序员充当专家，开发经理则作为门控机制（Gating）来选择专家。

为确保该系统高效运作，需满足以下条件：

每位程序员必须精通自身工作所需技能，同时所有程序员需能共同完成应用开发。
开发经理需充分了解所有程序员的专长，并能高效分配任务。

1.1 负载均衡

虽然稀疏门控G(x;Θ)能在不增加计算成本的情况下显著扩展模型参数空间，但其性能高度依赖门控机制的有效性。MoE的公式是“每遇到一个Token，就去找相应的Expert来计算”，但实际训练时是反过来的：先给每个Expert分配好相应的算力，然后将Token分配（Route）到所属的Expert中并行计算，这也就为什么负责打分的门控机制也被称为Router的原因。因为门控机制无法控制发给专家的token的概率，所以在实际操作中，会存在专家间工作负载分布不均衡的情况。某些专家被频繁使用（接收到了很多token）而其他专家却很少被调用（接收的token寥寥无几）。我们管这种现象叫expert负载不均衡。这不仅不符合MoE的设计初衷（术业有专攻），还影响计算效率（例如引起分布式训练中各卡通讯时的负载不均）。

要理解专家负载均衡，可以从batch size的角度出发。通常来讲，较大的 batch size 推理性能更好，但是由于样本在MoE层激活专家时需要并行，MoE层中每个专家的实际batch size会减少。举个例子，假设当前 batch 有10个token，其中5个token被路由到了某个专家网络，而其他5个token被路由到了其它5个不同的专家网络，这就会让各专家网络获得的 batch size 不均匀，一个专家的batch size是另外5个专家的5倍，导致另外5个专家利用率不足和硬件资源浪费。并且，如果我们把所有的token都发送给少数几个头部专家，训练效率将会变得低下：

假如前面几个token增加了这些被选择专家的门控权重，这反过来导致它们以更高的门控权重更频繁地被选择。这导致它们训练更多，它们的门控权重再次增加。这种情况会不断自我强化，因为受青睐的专家训练得更快、更充分，它的效果一直在被优化，因此选择它们的频率也会更高。那么此时，这几个少数专家就会过载，每次需要计算大量token，其他的专家模型就得不到训练而被闲置，就会导致工作负荷不足的专家会因为训练 tokens 不足，而难以学习有效知识。进而导致模型失衡，性能下降。
由于梯度冲突（gradient conflict），路由奔溃也会导致训练不稳定。超负荷工作的专家接收更多 input token，他们积累的梯度也会更大，因此，超负荷工作专家与负荷不足专家的梯度在幅值和方向上均可能发生偏离，导致训练难以收敛。

因此，MoE模型中需要控制专家均衡。为了对抗这种不平衡，人们实施了各种负载均衡技术，目的是确保所有专家在训练过程中大致承担相等的责任。我们在前一篇就介绍过，在门控中加入噪声机制可以避免反复路由到同一个专家，让门控在做出选择时跳过几个最优专家模型，去选择其余的专家模型，从而更好地协同工作。具体如下。

原始处理流程如下图标号1，其中门控函数是softmax。路由策略就是将输入乘以权重矩阵并应用 softmax。
但是，这种方法并不能保证专家的选择将是稀疏的。为了解决这个问题，我们首先对输入进行线性变换，然后再加上一个softmax，这样得到的是一个非稀疏的门控函数。对应下图标号2。
但是这样依然不够，因此我们在进行softmax之前，先使用一个topk函数，只保留最大的k个值，其他都设为-∞。这样对于非TopK的部分，由于值是负无穷，这样在经过Softmax之后就会变成 0，不会被选中，就得到了稀疏性。在这个基础上，我们在输入上再加上一个高斯噪声，迫使路由决策保持概率性。此处对应下图标号3。

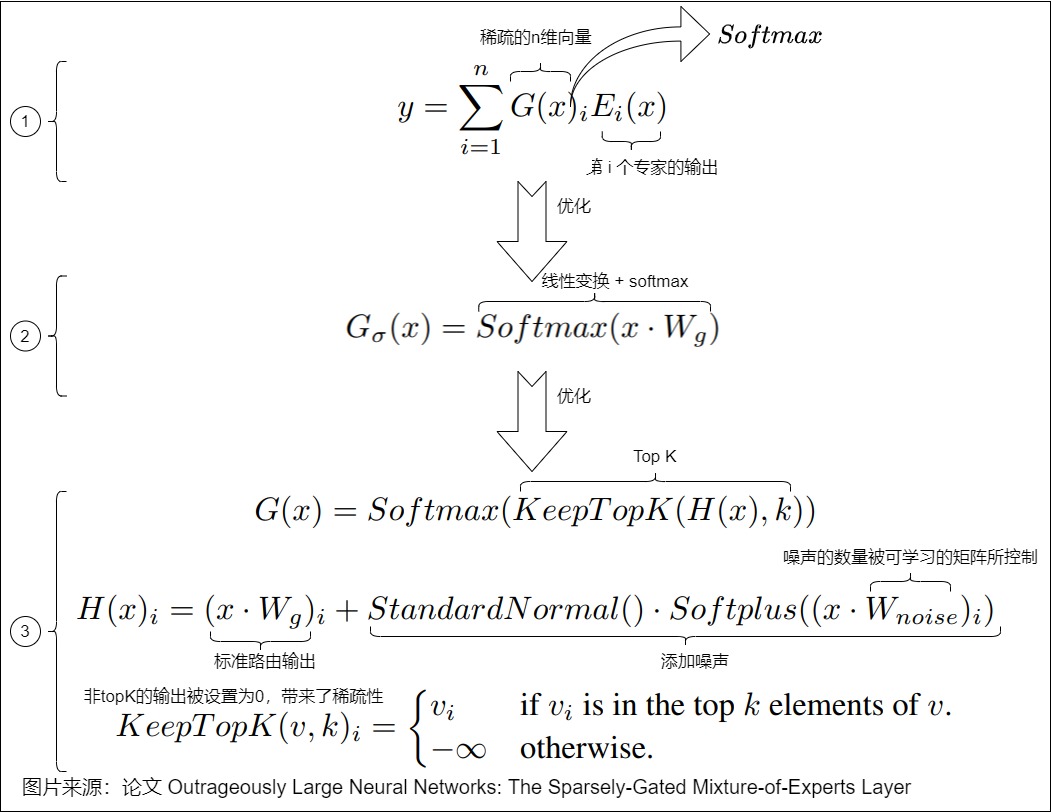
仅仅加入噪声是不够的，人们针对这一问题提出了多种解决方案。其中，最常用的策略是为负载均衡添加辅助损失函数（Auxiliary Loss）和基于专家来施加的一些策略，比如专家能力和专家选择（Expert Choice）。

本节后续介绍的知识点都是解决负载均衡的相关技术。

1.2 辅助损失函数

为了缓解负载失衡，人们在模型训练的目标函数基础上引入了辅助损失函数（auxiliary load balancing loss ），鼓励给予所有专家同等的重视，以促进每批次中令牌（token）在专家间的均匀分配，这些损失项被添加到训练目标中。

1.2.1 定义

论文"A Survey on Mixture of Experts"给出辅助损失函数的定义如下图，N 是专家数量，T 是 token 数量，K 是每个 input token 激活的专家数量。为确保T个令牌（token）在N个专家间的均匀分布，应最小化负载均衡损失函数。下图也给出了损失函数的最优情况，此时，每个专家都获得等量的分发token，Di = 1/N，以及相等的门控概率比例 Pi = 1/N。这样可以维持所有专家间的负载均衡，确保工作量均匀分布。

1.2.2 损失函数

因为辅助损失函数是在目标损失函数基础上引进的，所以我们先来看看损失函数。

最早的损失函数来自论文“Adaptive Mixture of Local Experts”。有两种损失函数，分别对应下图的标号1和2。其中，对于数据c， $p^c_i$ 是第 i 个专家占的比重，由门控网络控制， $o^c_i$ 是第 i 个专家的输出， $d^c$ 是最终期望的整体输出。

第一种方案有一个非常严重的问题，即不同的 expert 会互相影响，导致专家网络之间的强烈耦合。因为是所有专家网络的权重加总来共同计算损失的，一个专家权重的变化会影响到其他专家网络的loss。这种耦合可能会导致多个专家网络被用于处理每条样本，而不是专注于它们各自擅长的子任务。

为了解决这个问题，论文重新定义了损失函数，以鼓励专家网络之间的相互竞争，即方案2。直觉上改进就是每个 expert 单独计算 loss，多个 expert 的 loss 加权得到整体的 loss。这意味着，每个expert在处理特定样本的目标是独立于其他expert的。如果门控网络和expert都使用这个新的loss进行梯度下降训练，系统会倾向于将某类特定样本分配给特定的expert。因为当一个expert在给定样本上的的loss小于所有expert的平均loss时，它对该样本的门控score会增加；当它的表现不如平均loss时，它的门控score会减少。这种机制鼓励expert之间的竞争，而不是合作，从而提高了学习效率和泛化能力。

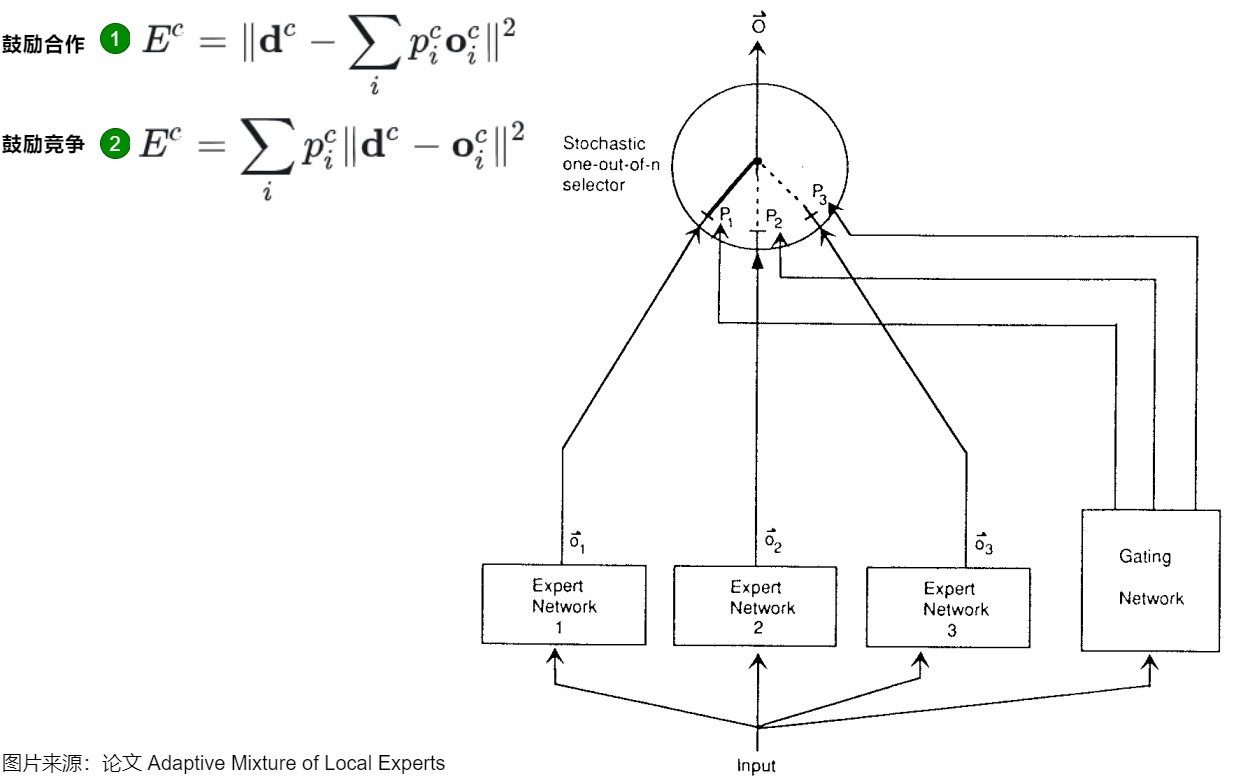
我们接下来看看如何增加辅助损失函数。

1.2.3 业界鼻祖

论文“Outrageously large neural networks: The sparsely-gated mixture-of-experts layer”就首创设计了额外的损失函数来促使所有专家具有同等的重要性，也首创了具有辅助负载平衡损失的可微分启发式方法，通过选择概率对专家输出进行加权，使门控过程可微分，从而能够通过梯度优化门控函数。这种方法随后成为MoE领域的主流研究范式。

论文先为每个专家定义了其相对于一批训练样本的重要性 Importance(X) ，即该专家在这批样本中门控值的总和，在批次中经常选择的专家将具有很高的重要性分数。然后定义了一个额外的损失函数 $L_{importance}(X)$ ，这个额外损失函数被添加到模型的整体损失函数中。这个损失函数等于重要性值集合的CV（coefficient of variation）平方（变异系数，可以度量一组数据的离散程度），乘以一个手动调整的缩放因子 $w_{importance}$ 。这个额外的损失鼓励所有专家在所有批次中具有相等的重要性。

虽然这种损失函数可以确保同等重要性，但专家可能仍然会收到数量截然不同的示例。例如，一位专家可能会收到一些权重较大的示例，而另一位专家可能会收到许多权重较小的示例。这可能会导致分布式硬件上的内存和性能问题。为了解决这个问题（鼓励每个expert拿到相同数量的样本进行计算），论文引入了第二个损失函数 $L_{load}$ 来进一步确保负载均衡。

具体计算公式推导如下图所示。

1.2.4 GShard

对于损失函数的设计，有一个简单的想法：例如有 S 个token，E 个专家，假设 $c_e$ 是第 e 个专家接受的token数量。如果MoE是负载均衡的，那么每个专家收到的token一样多，token比例 $\frac{c_e}{S}$ 应该是相同的。因此GShard把每个专家收到的token的平方和定义为负载均衡损失（见下图标号1），所有专家收到token比例都相等时， $l_{aux}$ 得到最小值。但是 $c_e$ 是从top-k函数中导出，不是可微的。而且，这样的辅助损失函数并不包含Gating函数的参数，无法训练进行梯度更新。于是GShard中引入了一个做法, 把平方项的一个分量 $\frac{c_e}{S}$ 替代成Gating softmax的均值 $m_e$ （见下图标号2），因为 $c_e$ 和 $m_e$ 有一定依赖关系，对 $m_e$ 的调整也会影响 $c_e$ ，从而实现对各专家负载分配的调节。

具体推导过程见下图。

为了进一步防止某些专家超负荷，GShard在训练时又引入以下概念：

专家容量 (Expert Capacity)，约为 $\approx \frac{2N}{E}$ （如果共有 N 个 token，E 个专家）。一旦某个专家被分配的 token 超过了这个容量，就可能丢弃一些 token（或者通过残差连接导入到下一层再处理）。
本地分组 (Local Groups)：不是所有 token 都在全局竞争，而是先进行分组后再分配给专家。这样能缩小混乱程度。

1.2.5 Switch Transformers

为了进一步防止 token 被丢弃，Switch Transformer 引入了简化版的辅助损失（类似 GShard 的辅助损失）来平衡重要性分数并在专家之间执行负载均衡，以希望每个专家从批次中获得的token数量大致相等。具体如下图所示，其中 α 是一个超参数，用于在训练过程中微调此损失的重要性。值过高会影响主要损失函数，而值过低则无法有效进行负载平衡。

该辅助损失函数不再计算变异系数，而是将分配的 token 数量与每个专家的路由概率进行加权比较。该损失相对于 P 是可微分的，并且可以很容易地纳入训练中，它鼓励分配给每个专家的token分数和分配给每个专家的路由概率分数都是 1/N，这意味着每个专家同样重要，并且接收到平衡数量的token。

1.2.6 通用思路

苏剑林大神给出了构建Aux Loss的通用思路：首先基于F构建符合要求的损失，然后在实现时将F替换成P+sg[F−P]。此处F是Expert当前的负载分布，而P则相当于F的一个光滑近似。sg[]是stop gradient算子，特点是保持前向输出不变，但强制梯度为零。假设 Q是均匀分布 $Q = (1/ n, 1/ n, ..., 1/ n)$ ，负载均衡等价于F=Q。下式就是一个比较直观的Aux Loss：
$L_{aux} = \frac{1}{2}||F-Q||^2 = \frac{1}{2}\sum^n_{i=1}(F_i-1/n)^2 \tag 1$
如果F是 $argtop_k$ 的输出，则上式并不是一个能直接用的可导目标，可以通过STE（Straight-Through Estimator）技巧来在在反向传播的时候将F替换成P。

另外，常见辅助负载均衡损失公式如下，其中n是expert个数，p是router输出的概率，f是每个expert在所有token上被topk取到的概率。
$L_{aux} = <f,p> = \sum^n_{i=1}f_ip_i \tag2$
公式(1)和公式(2)的梯度是等价的，这说明公式(2)可以使专家负载均衡化。

1.2.7 小结

下图是各种辅助损失函数及其典型系数配置概述。我们以粗体来标注每种辅助损失的作者，用下划线来表示对原始方案进行修改的优化者。

1.3 专家策略

1.3.1 专家能力

因为GShard和Switch Transformers都提到了专家能力（Expert Capacity，也叫做专家容量），而GShard的实现相对简单，因此我们以Switch Transformers为例来仔细学习下。

Switch Transformers的模型是面向TPU，其要求所有张量形状都是在编译期间内静态固定的。但因为路由是动态的，因此路由到每个专家的张量形状也是动态的。为了解决这一问题，Switch Transformers使用了专家容量（Expert Capacity）。如下图所示，专家容量为每个batch中总 Token 数除以专家数，然后再乘以容量因子（Capacity Factor），即可得到专家容量（每个专家对应的 Token 数）。该变量决定了可以路由到任何一个专家的最大token数量。如果当前专家接收到的token数已经超过了容量，那么它就不再接收token了，此时我们称这些路由到已满容量的专家的token为溢出token。

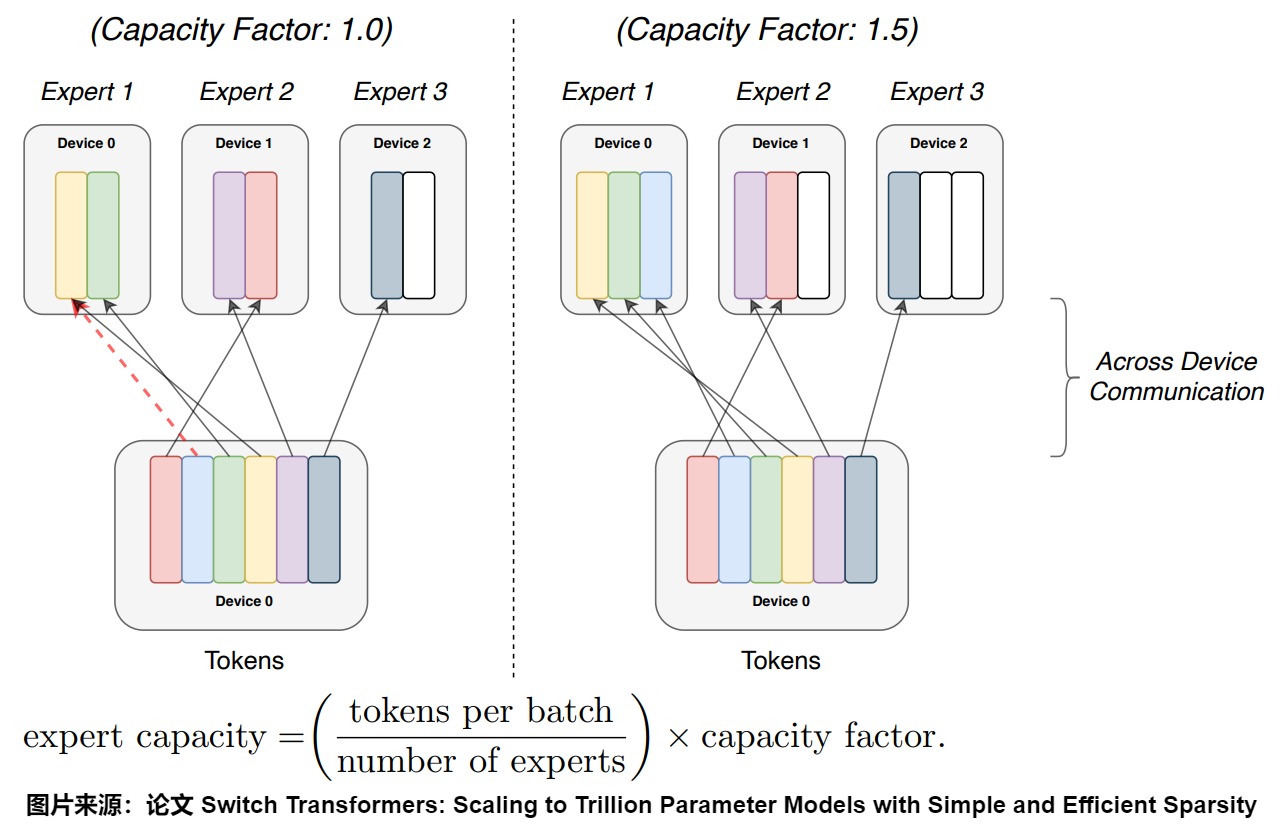
针对专家容量，Switch Transformers也引入了两种处理策略：

Zero padding。因为存在容量，所以Switch Transformers给每个专家设定了一个Expert buffer用来接收在容量范围内的token。如果某些专家的Expert buffer没有填充满，则使用0向量填充，我们称为Zero padding。具体而言，最终每个expert上的输入数据维度为(E, C, M)，其中C表示capacity。这样可以保证每个expert上要处理的输入数据维度是一样的，这有利于硬件层面的后续处理。
Drop tokens。如果向单个专家发送了太多token（即超出专家能力），致使某个专家发生溢出情况，Switch Transformers会跳过这些token的计算。这些token被通过残差连接直接传递到下一层。因为这些token没有经过专家处理，因此是一种信息损失。

Zero padding和Drop tokens是一体两面。缩小容量会减少Zero padding，但是会因为 token 溢出而导致模型性能下降。扩大容量可以缓解Drop tokens，但过大的容量会引起更严重的zero padding问题（影响到矩阵的稀疏程度），无效计算越多，浪费计算资源。另外，负载越不均衡，需要 Padding 的 Token 也就越多，无效计算越多，丢弃的token也可能更多。

从上图也可以看出，容量因子越大，需要 Padding 的 Token 也就越多，无效计算越多；负载越不均衡，需要 Padding 的 Token 也就越多，无效计算越多。为了更好的负载均衡，作者同样添加了 Load Balancing Loss。上图有 6 个 Token，3 个专家，我们分别看看两种不同的专家容量设置情况。

容量因子为 1.0：如上图左侧所示，对应的专家容量为 2：
- Expert 1有 3 个 Token，则需要丢弃一个token，或者把该token通过残差连接直接传到下一层。
- Expert 2 有 2 个 Token，恰好等于专家容量。
- Expert 3只有 1 个 Token，需要填充 1 个空的 Token。
容量因子为 1.5：如上图右侧所示，对应的专家容量为 3：
- Expert 1 有 3 个 Token，恰好等于专家容量。
- Expert 2 只有 2 个 Token，需要填充 1 个空的 Token。
- Expert 3 只有 1 个 Token，需要填充 2 个空的 Token。

对于填充，我们可以使用掩码来进行处理，假设 S = batch_size * seq_len，E代表专家数目，C表示capacity（Expert buffer），则之前的门控网络的输入是：(S, embedding_size)，输出是 (S, E)。含有容量处理的门控网络的输入是(S, embedding_size)，输出是：

combine_weights = (S, E, C)。表示对 S 个token中每个 token 而言，它去到每个专家的概率。而这个概率按照该token在buffer中的位置（C）存放，不是目标位置的地方则用0填充。比如[[[p1, 0, 0]], [0, p2, 0], [0,0,0]]，表示第一个token会去两个专家，去第一个专家的概率是p1，去第二个专家的概率是p2。
dispatch_mask = (S, E, BF)。combine_weights 为0的地方设为False，为1的地方设为True，填充时候会用到mask。

我们用实际例子来看看。假设的输入

• Token 数 S = 3

• Expert 数 E = 4

• Buffer 长度 C = 3（每个专家最多接收 3 个 token）

• Embedding 维度 M = 512

reshape_input (𝑆=3,C=2) ：

Token A → [a1,..., a2]  # token的特征维度是512
Token B → [b1,..., b2]
Token C → [c1,..., c2]

获取top 2之后的prob如下：

combine_weights (S=3, E=4, C=3)：
[
    [[0, 0, 0], [0.57, 0, 0], [0, 0, 0], [0.43, 0, 0]],    # Token A 发给了专家1，3
    [[0, 0, 0], [0.75, 0, 0], [0.25, 0, 0], [0, 0, 0]],    # Token B 发给了专家1，2
    [[0.375, 0, 0], [0, 0, 0], [0.625, 0, 0], [0, 0, 0]]   # Token C 发给了专家0，2
]

mask 如下：

dispatch_mask (S=3, E=4, C=3)：
[
    [[0, 0, 0], [1, 0, 0], [0, 0, 0], [1, 0, 0]],  # Token A 发给了专家1，3
    [[0, 0, 0], [1, 0, 0], [1, 0, 0], [0, 0, 0]],  # Token B 发给了专家1，2
    [[1, 0, 0], [0, 0, 0], [1, 0, 0], [0, 0, 0]]   # Token C 发给了专家0，2
]

mask 会和输入 token 合作，按照专家的 buffer 顺序排列 token，形成 dispatched_expert_input。

dispatched_expert_input (E=4, C=3, m=512)：
[
    [[c1,..., c2], [0, 0], [0, 0]],    # Expert 0 接收到了 token C
    [[a1,..., a2], [b1,..., b2], [0, 0]],  # Expert 1 接收到了 token A 和 B
    [[b1,..., b2], [c1,..., c2], [0, 0]],  # Expert 2 接收到了 token B 和 C
    [[a1,..., a2], [0, 0], [0, 0]]     # Expert 3 接收到了 token A 
]

接下来进行专家计算。

expert_outputs (E=4, K=3, C=2)：
[
    [[c1,..., c2], [0, 0], [0, 0]],      # Expert 0
    [[a1,..., a2], [b1,..., b2], [0, 0]],  # Expert 1
    [[b1,..., b2], [c1,..., c2], [0, 0]],  # Expert 2
    [[a1,..., a2], [0, 0], [0, 0]]       # Expert 3
]

最后使用expert_outputs 和prob进行加权求和。

1.3.2 专家选择

在 MoE 的 Routing 中有两种选择方案，Token-Choice 和 Expert-Choice：

目前大部分主流的MoE模型都是token choice routing（或者直接叫top-k routing），即根据输入token和所有专家的匹配程度计算出affinity matrix，然后对affinity matrix应用 Softmax 计算，选择匹配度最高的k个专家进行处理，最后以加权和作为对应token的输出。这种方案有几个缺陷：

负载不平衡：我们无法控制每个专家接收的 token 数量，会造成token分配不均。部分专家被分配的token过少导致训练、利用得不够充分；部分专家被分配的token过多，但由于内存限制只能选择一定数量的token使用，导致token资源的浪费。负载不平衡也会损害步长延迟，从而影响推理时间，因为步长延迟可以由负载最大的专家确定。很多方法在负载平衡上增加了辅助损失，以缓解这个问题。然而，这种辅助损失并不能保证负载的平衡，尤其是在训练的重要早期阶段。
冗余专业化/专业化不足（Under Specialization）：每个MoE层都使用一个门控网络来学习令牌与专家的亲和力。理想情况下，学习的门控网络应该产生亲和力，以便将相似或相关的令牌路由到同一个专家。然而，如果门控网络是次优策略，则可能会产生冗余的专家和/或不够专业的专家。
Same Compute for Every Token。在令牌选择策略中，每个令牌恰好接收k个专家，因此占用相同的计算量。然而这并不一定是正确的。token的重要性是不同的，MoE模型应该根据输入的复杂性灵活分配其计算资源。

expert choice routing（EC）与token choice routing相反，是让每个expert选择当前所有输入token（比如一个batch）中和自身匹配度最高的k个token来处理。下图是从Expert-Choice论文中摘录出来的，左边蓝色两个是Conventional MoE，右面是expert choice MoE。

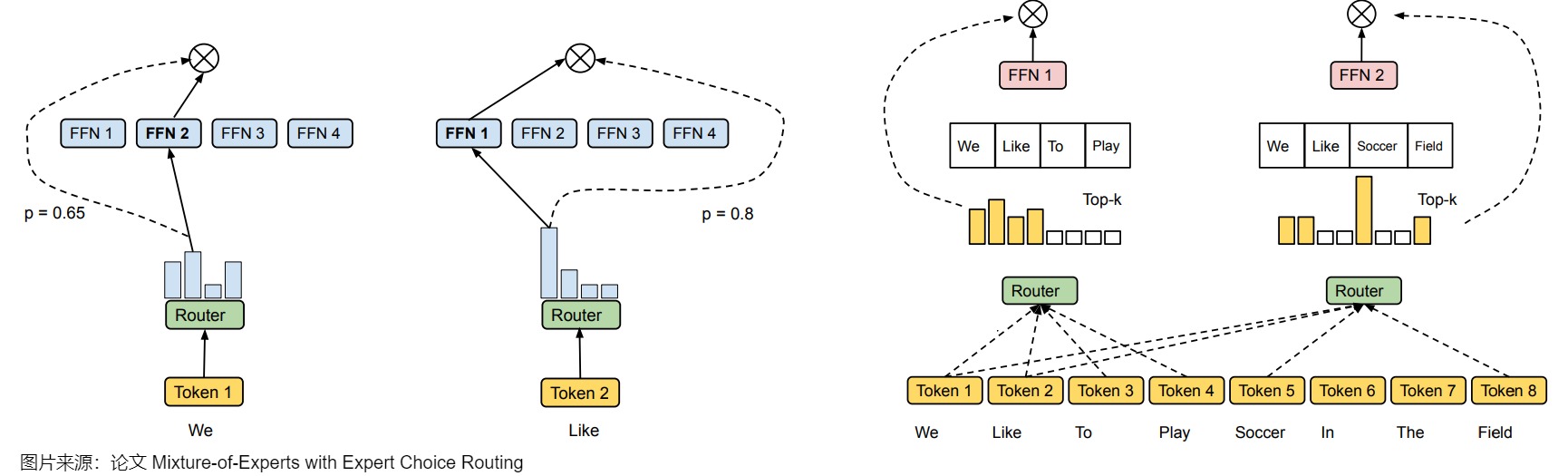
下图会更加清晰。

Token-Choice：如左图所示，每个 Token 都来选择要经过哪些专家，这种方式会存在负载不均衡的问题，因为可能出现多个 Token 都选择了一个专家，超过容量限制，不得不丢弃，而与此同时有些专家的 Token 很少，可能还需要 Padding。
Expert-Choice：如右图所示，每个专家都来选择要使用该专家的 Token，这样每个专家通过的 Token 数都是相同的，但是可能出现某些 Token 使用了多个专家，而有些 Token 只使用了很少甚至 0 个专家的情况。

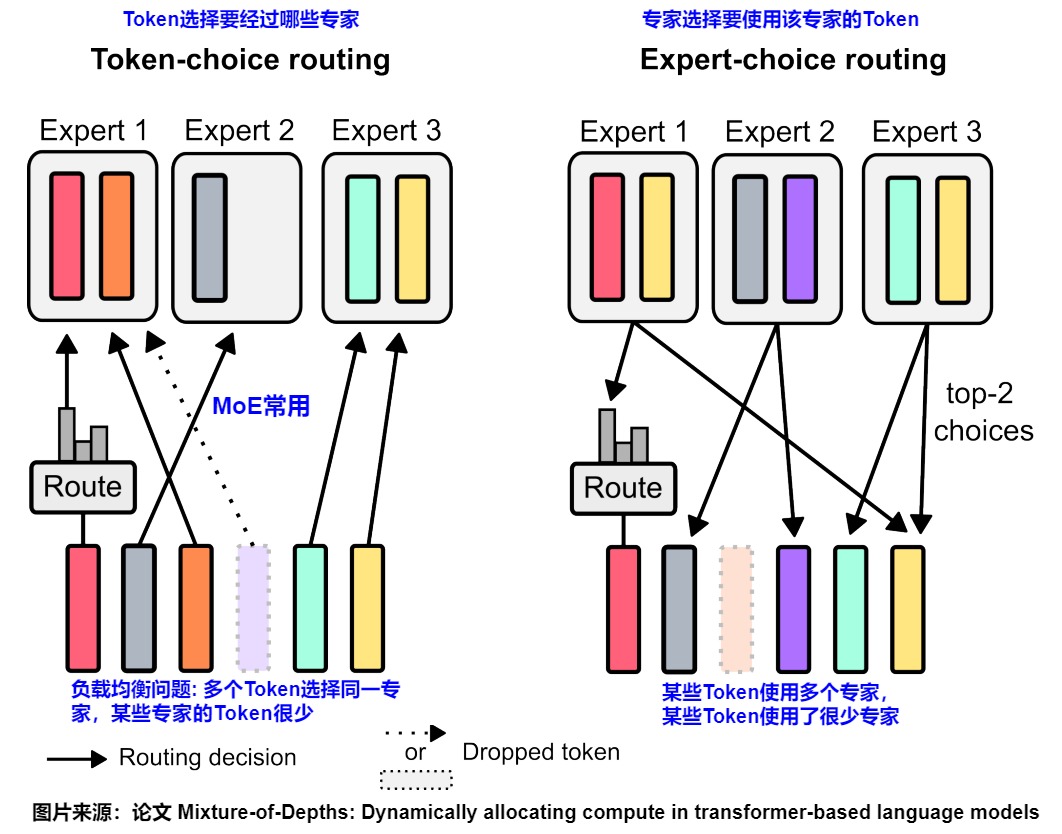
算法和推导如下图所示。

Expert Choice 这种方法也存在局限 —— 未来 token 泄露问题。由于每个专家需要先查看所有 token 的路由分数才能决定处理哪些 token，这违反了因果关系（causality）。

0x02 DeepSeek V1

2.1 背景&动机

尽管MoE架构有着很大潜力，但现有的MoE架构可能存在知识混杂（Knowledge Hybridity）和知识冗余（Knowledge Redundancy）的问题，限制了专家的专业化，具体如下：

知识混杂。分配给特定专家的token可能会涵盖不同知识，因此，指定的专家将倾向于在其参数中汇集不同类型的知识，这些知识很难同时利用。知识混合问题出现在专家数量有限的场景下，在这种情况下，每个专家需要处理过于广泛的知识领域，这就产生了知识混合性，从而阻碍了专家们在特定领域进行深入，导致很多 expert 不是真正的专家，而是杂糅了各种知识的混合体，不能发挥 expert 的专业作用。
知识冗余。当 MoE 模型中的不同专家学习到相似的知识时，就会出现知识冗余，这与模型设计初衷相违背。这是因为，分配给不同专家的token可能需要一些共同知识来进行处理，因此，多个专家可能会在训练中将各自的某些参数收敛到一些共享知识，从而导致专家参数中的冗余。而模型整体容量有限，冗余就造成 MoE 模型整体性能下降。
分裂。MoE架构潜的潜力其实依赖于“专家”的专精度，每个专家应该获得不同领域的非重叠且集中的知识。如果不能在内部世界模型上做到对齐和互换，MoE其输出将是一个人格分裂的结果。此处的内部世界模型指的是麻省理工学者（“Platonic Representation Hypothesis”）讲的“现实的共享统计模型”，也等同“以概率为表征的丰富范畴”，模型越大越丰富越准确。

其实，这就是Knowledge Specialization和Knowledge Sharing之间如何权衡的问题。

Knowledge Specialization意思是每个专家能够获取不重叠且聚焦的知识。
Knowledge Sharing意思是通过门控网络与协同机制，使不同专家在独立处理特定任务的同时，仍能共享底层知识或通用特征，从而提升模型的整体性能和效率。

追求通才可能牺牲技能深度，追求专精又无法舍弃通用知识，因为我们很难界定MoE中，每个专家的专精程度及他们掌握的通用知识范围的边界。这个问题共同阻碍了现有MoE实践中的专家专业化，使其无法达到MoE 模型的理论上限性能。

2.2 解决方案

为了解决上述问题，DeepSeek-MoE 引入了“细粒度/垂类专家”和“共享专家”的概念。

“细粒度/垂类专家” 是通过细粒度专家切分 (Fine-Grained Expert Segmentation) 之后得到的专家。在保持整体参数量不变的情况下，DeepSeek-MoE将一个 FFN 再切分成更细的粒度，构建更多的专家。该技术的想法非常简单：如果有更多专家被激活，那么处理某个 token 所需的知识就更有可能被分解并由不同专家获取。通过增加专家数量和减少专家的参数量，可以降低每个专家负责的主题数量，使得每个专家更专注于其领域，从而提高模型在各个领域的专业性和准确性，应对更广泛和复杂的主题。此外，增加专家数量也会增加可能的专家组合数量，从而提高了模型对不同输入的适应能力和泛化能力。
“共享专家（shared expert）”是掌握更加泛化或公共知识的专家。尽管增加专家数量可以提高模型的专业性，但过于专业化的专家可能无法涵盖足够广泛的主题，从而限制了模型的应用范围。引入共享专家就可以解决过度专业化的问题，通过将共享知识压缩到选出的共享专家中，将减少每个细粒度专家中的知识冗余，确保每个路由专家通过聚焦于特定领域保持专精。共享专家的数量是固定的且总是处于被激活的状态，无论路由器模块如何计算，每个token都将分配给这些共享专家。这样模型可以在保持广泛知识的同时，确保在每个预测中都能涉及到适当的专业领域。

回到前面招聘程序员的例子，“细粒度/垂类专家” 就是把前台和后台的工作做进一步细化，比如后台分为：若干服务器开发程序员，若干大数据处理程序员等。“共享专家”就是专门设置DBA角色，统一为服务器开发同学提供数据库支持。

下图来自 deepseekMoE 论文，图上 (a) 展示了一个具有传统 top-2 路由策略的 MoE 层。子图 (b) 说明了细粒度专家分割策略，k=4。随后，子图 © 是DeepSeekMoE架构中带有共享专家隔离策略的路由方案。这里，“k”位专家是固定的，也就是说他们始终会针对每个预测运行。这些“共享专家”或专家掌握广泛的知识，而超专业专家（对于此特定模型最多可达 64 位）掌握更细粒度的知识。

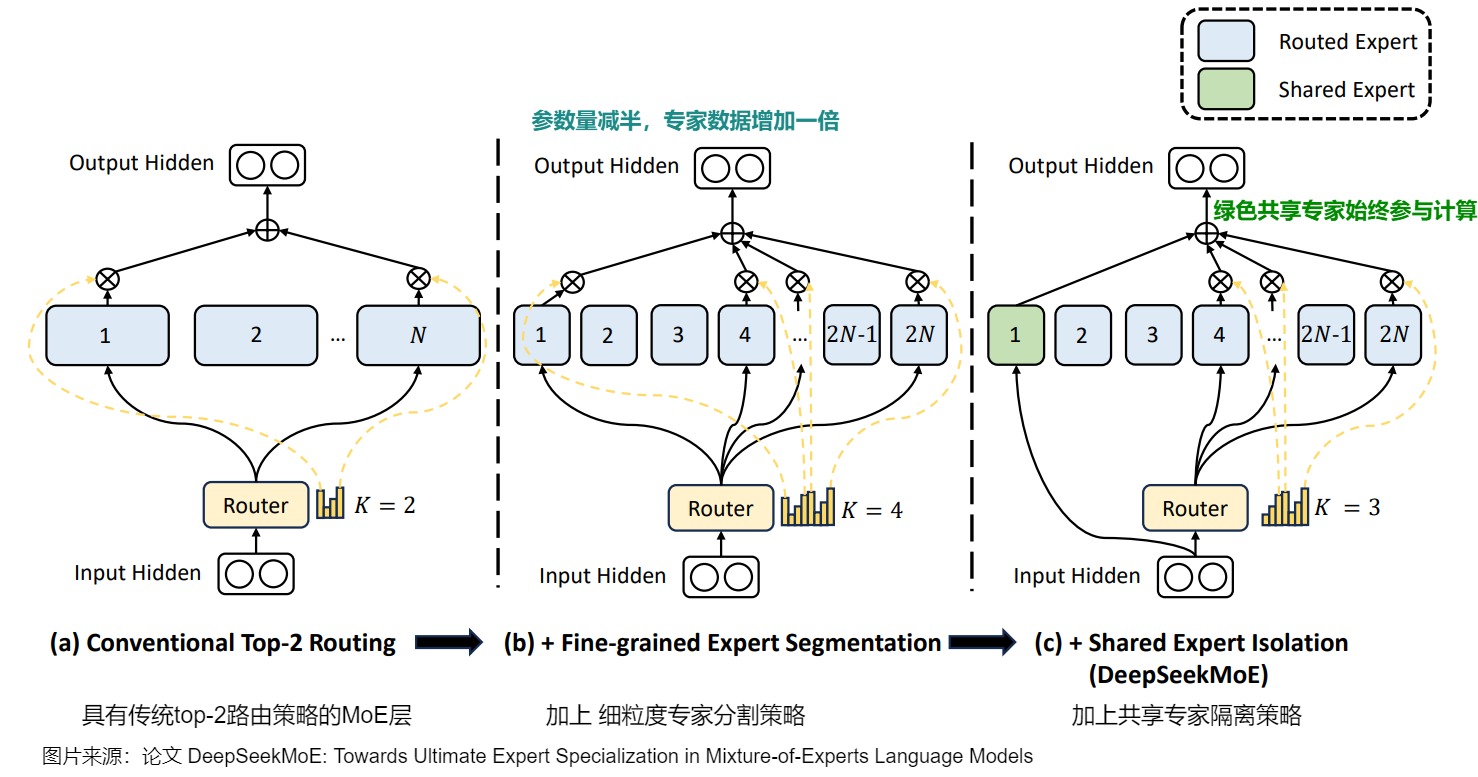
下图给出了DeepSeekMoE架构的公式形式，以及和vanilla Transformer，native MoE的对比。其中，

mN 表示所有子专家（细粒度专家）的总数。相当于通过将FFN中间隐藏层的维度减少到原来的1/m，来把 expert 的个数从 N 个提升为 mN 个，同时激活的专家数量也从 k 个提升为 mk 个。
$g_{i,t}$ 是针对第个专家在第个 token 上的门控权值。
$FFN_i$ 表示 N 个专家中的第 i 个专家。
$u^l_t$ 和 $h^l_t$ 是第 l 个Transformer层中第 t 个Token的输入隐藏状态和输出的隐藏状态。
$e^l_i$ 通常被称为第i个专家的质心，其计算方式是通过聚合历史上被路由到该专家的所有输入token来得到一个平均值。 $u^l_t$ 与 $e^l_i$ 之间的内积衡量了当前输入token与历史上被路由到第i个专家的平均输入token的相似程度。直观上，若第i个专家处理过大量与当前token相似的输入，则它应更擅长处理当前token。
$s_{i,t}$ 是token和专家之间的亲和度（affinity），即第 t 个 token 在第 i 个专家上的打分。相似度通过Softmax函数将该内积转换为概率分布。由于存在N个专家，因此每个token会对应N个 $s_{i,t}$ ，表示该token对各专家的亲和度或者倾向程度。该机制通过可学习的路由参数动态分配token到专家，并与模型整体联合训练。

路由机制会从所有细粒度专家中为每个 token 选出前 mK 个得分最高的专家。

2.3 负载均衡

自动学习的路由策略可能会遇到负载不平衡的问题，这会导致两个显著的缺陷：

路由崩溃的风险，即模型始终选择少数几个专家，其他专家缺乏充分训练；
如果专家分布在多个设备上，负载不平衡会加剧计算瓶颈。

因此，DeepSeek 引入了两个损失函数，具体见下图。 $f_i$ 表示路由到专家的 token 占比， $P_i$ 表示专家的平均路由概率（gating probability）。 $\alpha_1$ 是损失系数。D 表示设备数， $f'_i$ 与 $P'_i$ 分别表示设备上所占的平均 token 比例和平均路由概率。 $\alpha_2$ 则是另一层的损失系数。这种损失相对于 P 是可微分的，并且可以很容易地纳入训练中，它鼓励分配给每个 EA 的标记分数和分配给每个 EA 的路由器概率分数为 1/N，这意味着 EA 同样重要，并且接收到平衡数量的标记。通过这种双重均衡损失设计，DeepSeekMoE 能在保证专家内部细粒度专长化的同时，尽量避免某些专家或某些设备被过度使用，进而减小路由不均带来的计算瓶颈。

2.3.1 专家级负载损失（Expert-Level Balance Loss）

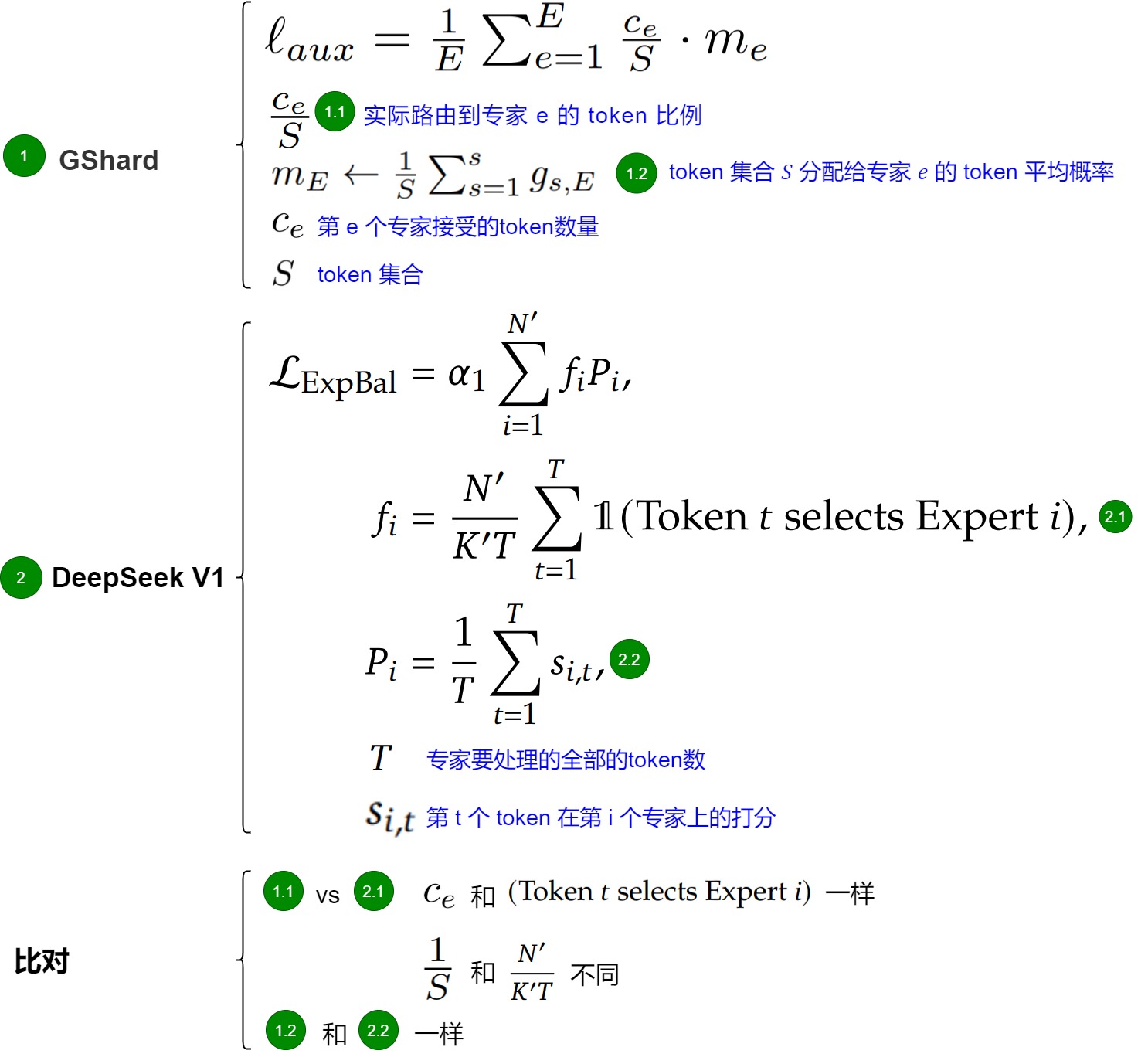
引入专家级负载损失的目的是：保证在专家之间分配的均衡性，保持计算损失的恒定，让损失不随专家数量的变化而变化。下图把GShard和 DeepSeek V1的损失函数进行比对，可以发现图上：

标号1.1 和 2.1 中，只有 $\frac{1}{S}$ 和 $\frac{N'}{K'T}$ 不同。
标号1.2 和 2.2 相同。

因此我们看看，标号2.1中，为何分子多乘了个路由专家数（N′ )，分母上多除了个激活路由专家数（K′ ）。

理想状态下，如果token是均匀分配，每个token激活 K′ 个专家。共 TK′ 个token 会平均分配给了 N′ 个专家。每个专家被分配的token数为 TK′/N′ 。则：

$f_i$ 是专家 i 被分配的 token 数量比率（fraction of tokens sent to expert i），在这种情况下应该是 K′/N′ 。
𝑃i 是门控函数分配给专家 i 的门控分数的比率（fraction of router probability allocated to expert i），在这种情况下应该是 1/N′。

把这两个带入到 $L_{ExpBal}$ 中，得到最终loss里面有个 K′/N′ 项，该项是随着路由专家数（ N′ ）和激活路由专家数（ K′ ）动态变化而变化的，这就是问题所在。为了去掉这个动态变化的项，让Loss维持一个恒定的量级，V1版本对辅助loss整体乘以 N′/K′ ，以保持loss计算是不随专家数变化而变化的。这样可能是为了调参和做比对更加简单。

2.3.2 设备级负载损失（Device-Level Balance Loss）

DeepSeek 会将专家分成 D 组，每组专家放在一个设备上。设备级负载损失用来确保在不同 GPU 或设备之间的计算负载也是均衡的。在损失超参数 $\alpha_1,\alpha_2$ 设计上, 专家负载均衡损失参数设置的较小，而设备负载均衡损失的超参数设置较大，设备级负载loss 比专家级粒度更大，相当于在多组专家间做负载均衡，这样可以更好地平衡不同设备的计算负载。

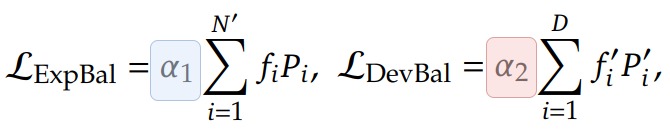
2.4 实现

模型结构如下。

(mlp): DeepseekMoE(
  (experts): ModuleList(
    (0-159): 160 x DeepseekMLP(
      (gate_proj): Linear(in_features=5120, out_features=1536, bias=False)
      (up_proj): Linear(in_features=5120, out_features=1536, bias=False)
      (down_proj): Linear(in_features=1536, out_features=5120, bias=False)
      (act_fn): SiLU()
    )
  )
  (gate): MoEGate()
  (shared_experts): DeepseekMLP(
    (gate_proj): Linear(in_features=5120, out_features=3072, bias=False)
    (up_proj): Linear(in_features=5120, out_features=3072, bias=False)
    (down_proj): Linear(in_features=3072, out_features=5120, bias=False)
    (act_fn): SiLU()
  )
)

关键代码如下。从源码中看，MoEGate函数的实现和论文是有一些差异的，是对针对一个batch内的所有token进行负载均衡损失计算，即 T 就是一个Batch的总token量。torch.topk()函数会返回输入张量中指定维度上的前 k 个最大元素以及其对应的索引。

class MoEGate(nn.Module):
    def forward(self, hidden_states):
        bsz, seq_len, h = hidden_states.shape        
        # 公式里的T，是一个Batch数据的全部token做计算，每个Batch会重新计算
        hidden_states = hidden_states.view(-1, h)
        
        logits = F.linear(hidden_states, self.weight, None)
        scores_for_aux = logits.softmax(dim=-1)
        
        topk_weight, topk_idx = torch.topk(scores_for_aux, k=self.top_k, dim=-1, sorted=False)
        topk_idx_for_aux_loss = topk_idx.view(bsz, -1)
        # 对选定的专家进行独热编码以创建专家掩码，将用于索引哪个专家将被调用
        mask_ce = F.one_hot(topk_idx_for_aux_loss.view(-1), num_classes=self.n_routed_experts)
        ce = mask_ce.float().mean(0)
        # 计算Pi，fi 和 aux_loss。这里的计算并没有跨Batch累积，每个Batch单独计算    
        Pi = scores_for_aux.mean(0)
        fi = ce * self.n_routed_experts
        aux_loss = (Pi * fi).sum() * self.alpha

0x03 DeepSeek V2

DeepSeek-V2进一步扩大了细粒度专家选择，采用了路由专家160选6，加上2个共享专家的做法，同时新增了一个路由机制和两个负载均衡方法。

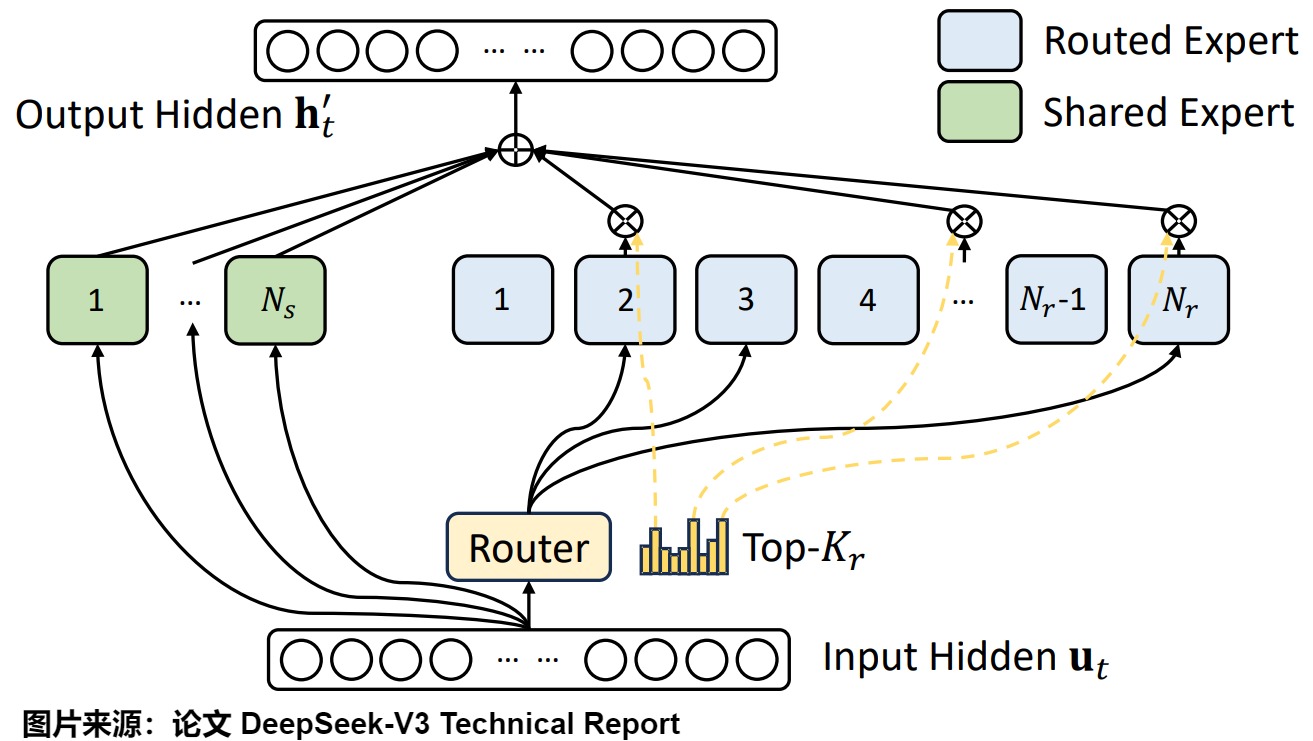
3.1 负载均衡

相对于DeepSeek-V1-MoE，对MoE模块主要在负载均衡上做了三方面升级。

设备受限的专家路由机制（Device-Limited Routing）

在专家并行时，MoE层的多个专家将被分配在多个设备上来并行训练。由于DeepSeek的MoE是做了细粒度专家的设计，通常专家会很多（V2模型的路由专家数有160个，激活专家6个）。如果专家是随机分布在不同的设备上，那么对每一个 token 有可能激活的专家会涉及大多数的设备，MoE的通信成本会非常高。

为了解决这个问题，DeepSeekV2 引入了设备受限的专家路由机制。具体说就是要求每个Token最多只能被路由到 M（M 小于 TopK）个设备上，以此来控制通信成本。具体做法分2步：

对于每个token，首先选择门控分数 $s_{i,t}$ 最高的专家所在的 M 个设备。
然后在这 M 个设备上的所有专家中选择 topK 个专家。

DeepSeek实际验证出，当 M≥3 的时候，这种受限的选 TopK 的操作，与不受限的全局选 TopK 的操作，模型效果上是大致相当的。所以在V2模型上，DeepSeek选择的 TopK=6，M=3 。

通信负载均衡损失（Communication Balance Loss ）

通过上面设备受限的路由机制可以减轻从输入侧将数据分发到多设备，减少多扇出的通讯量。但是在设备接收侧可能还是会出现集中几个设备的专家被激活的问题（即，单个设备接受的token比其它设备多），导致通信拥堵的问题。所以相对于V1，V2版模型增加了通信负载均衡的loss。

其中， Ei 表示第 i 个设备的一组专家，D 是设备数，M 是受限路由的设备数，T 是一个Batch的token数， $\alpha3$ 是该辅助loss的超参。对于 $f_i^{''}$ 的计算，乘以 D 和除以 M 也是为了保证loss不受到设备数量或者路由配置的影响。

设备受限的专家路由机制和通信负载均衡loss，都是为了解决通信负载平衡的方法。不同的是：设备受限的专家路由机制是在通信分发端确保分发的一个上限；而通信负载均衡loss是在通信接收端确保接收的平衡，鼓励每个设备接收等量的token。所以通过这两种方法，可以确保设备输入、输出的通信负载均衡。

设备级Token丢弃策略（Token-Dropping Strategy）

虽然多个负载均衡的loss（包括专家，设备，通信）能引导模型做通信和计算的平衡，但并不能严格做到负载均衡，接收设备侧还是可能出现集中到几个专家激活，导致通信阻塞的情况。为了进一步做计算的负载均衡。引入了设备级的Token丢弃策略。具体做法：

首先对于一个Batch输入token，算出每个设备的平均接收的token量，用这个数字作为设备的容量上限 C。
对于每个设备实际分配的token量 Td ，按照路由分数降序排列。
如果 Td>C 则将超过容量 C 的尾部token丢弃掉，对于超过容量的部分不进行MoE的Expert专家网络计算，直接送入上层Transformer网络，参与上层的计算。即在本层只有残差部分的结果，在另外一些层可能会参与专家计算。

作者为了保持推理和训练的一致性，在训练阶段也保持有10%的样本是不做Token丢弃的，来保证在推理阶段不做token丢弃的效果。

3.2 实现

V2版本的代码如下。

class DeepseekV2MoE(nn.Module):
    """
    A mixed expert module containing shared experts.
    """

    def __init__(self, config):
        super().__init__()
        self.config = config
        self.num_experts_per_tok = config.num_experts_per_tok

        if hasattr(config, "ep_size") and config.ep_size > 1:
            assert config.ep_size == dist.get_world_size()
            self.ep_size = config.ep_size
            self.experts_per_rank = config.n_routed_experts // config.ep_size
            self.ep_rank = dist.get_rank()
            self.experts = nn.ModuleList(
                [
                    (
                        DeepseekV2MLP(
                            config, intermediate_size=config.moe_intermediate_size
                        )
                        if i >= self.ep_rank * self.experts_per_rank
                        and i < (self.ep_rank + 1) * self.experts_per_rank
                        else None
                    )
                    for i in range(config.n_routed_experts)
                ]
            )
        else:
            self.ep_size = 1
            self.experts_per_rank = config.n_routed_experts
            self.ep_rank = 0
            self.experts = nn.ModuleList(
                [
                    DeepseekV2MLP(config, intermediate_size=config.moe_intermediate_size)
                    for i in range(config.n_routed_experts)
                ]
            )
        self.gate = MoEGate(config)
        if config.n_shared_experts is not None:
            intermediate_size = config.moe_intermediate_size * config.n_shared_experts
            self.shared_experts = DeepseekV2MLP(
                config=config, intermediate_size=intermediate_size
            )

    def forward(self, hidden_states):
        identity = hidden_states
        orig_shape = hidden_states.shape
        topk_idx, topk_weight, aux_loss = self.gate(hidden_states)
        hidden_states = hidden_states.view(-1, hidden_states.shape[-1])
        flat_topk_idx = topk_idx.view(-1)
        if self.training:
            hidden_states = hidden_states.repeat_interleave(
                self.num_experts_per_tok, dim=0
            )
            y = torch.empty_like(hidden_states)
            for i, expert in enumerate(self.experts):
                # 遍历模型中的所有可用专家并在每个专家上执行计算
                y[flat_topk_idx == i] = expert(hidden_states[flat_topk_idx == i])
            y = (y.view(*topk_weight.shape, -1) * topk_weight.unsqueeze(-1)).sum(dim=1)
            y = y.view(*orig_shape)
            y = AddAuxiliaryLoss.apply(y, aux_loss)
        else:
            y = self.moe_infer(hidden_states, topk_idx, topk_weight).view(*orig_shape)
        if self.config.n_shared_experts is not None:
            y = y + self.shared_experts(identity)
        return y

    @torch.no_grad()
    def moe_infer(self, x, topk_ids, topk_weight):
        cnts = topk_ids.new_zeros((topk_ids.shape[0], len(self.experts)))
        # scatter_()是原地操作函数，依据给定的索引，把源张量中的元素分散到目标张量的指定位置，第一个参数 1 代表在行上操作，操作是把第三个参数 1 赋值到第二个参数 topk_ids 指向的位置上
        cnts.scatter_(1, topk_ids, 1)
        tokens_per_expert = cnts.sum(dim=0)
        idxs = topk_ids.view(-1).argsort()
        sorted_tokens = x[idxs // topk_ids.shape[1]]
        sorted_tokens_shape = sorted_tokens.shape
        if self.ep_size > 1:
            tokens_per_ep_rank = tokens_per_expert.view(self.ep_size, -1).sum(dim=1)
            tokens_per_expert_group = tokens_per_expert.new_empty(
                tokens_per_expert.shape[0]
            )
            dist.all_to_all_single(tokens_per_expert_group, tokens_per_expert)
            output_splits = (
                tokens_per_expert_group.view(self.ep_size, -1)
                .sum(1)
                .cpu()
                .numpy()
                .tolist()
            )
            gathered_tokens = sorted_tokens.new_empty(
                tokens_per_expert_group.sum(dim=0).cpu().item(), sorted_tokens.shape[1]
            )
            input_split_sizes = tokens_per_ep_rank.cpu().numpy().tolist()
            dist.all_to_all(
                list(gathered_tokens.split(output_splits)),
                list(sorted_tokens.split(input_split_sizes)),
            )
            tokens_per_expert_post_gather = tokens_per_expert_group.view(
                self.ep_size, self.experts_per_rank
            ).sum(dim=0)
            gatherd_idxs = np.zeros(shape=(gathered_tokens.shape[0],), dtype=np.int32)
            s = 0
            for i, k in enumerate(tokens_per_expert_group.cpu().numpy()):
                gatherd_idxs[s : s + k] = i % self.experts_per_rank
                s += k
            gatherd_idxs = gatherd_idxs.argsort()
            sorted_tokens = gathered_tokens[gatherd_idxs]
            tokens_per_expert = tokens_per_expert_post_gather
        tokens_per_expert = tokens_per_expert.cpu().numpy()

        outputs = []
        start_idx = 0
        for i, num_tokens in enumerate(tokens_per_expert):
            end_idx = start_idx + num_tokens
            if num_tokens == 0:
                continue
            expert = self.experts[i + self.ep_rank * self.experts_per_rank]
            tokens_for_this_expert = sorted_tokens[start_idx:end_idx]
            expert_out = expert(tokens_for_this_expert)
            outputs.append(expert_out)
            start_idx = end_idx

        outs = torch.cat(outputs, dim=0) if len(outputs) else sorted_tokens.new_empty(0)
        if self.ep_size > 1:
            new_x = torch.empty_like(outs)
            new_x[gatherd_idxs] = outs
            gathered_tokens = new_x.new_empty(*sorted_tokens_shape)
            dist.all_to_all(
                list(gathered_tokens.split(input_split_sizes)),
                list(new_x.split(output_splits)),
            )
            outs = gathered_tokens

        new_x = torch.empty_like(outs)
        new_x[idxs] = outs
        final_out = (
            new_x.view(*topk_ids.shape, -1)
            .type(topk_weight.dtype)
            .mul_(topk_weight.unsqueeze(dim=-1))
            .sum(dim=1)
            .type(new_x.dtype)
        )
        return final_out

DeepseekV2MLP类的代码如下。

class DeepseekV2MLP(nn.Module):
    def __init__(self, config, hidden_size=None, intermediate_size=None):
        super().__init__()
        self.config = config
        self.hidden_size = config.hidden_size if hidden_size is None else hidden_size
        self.intermediate_size = (
            config.intermediate_size if intermediate_size is None else intermediate_size
        )

        self.gate_proj = nn.Linear(self.hidden_size, self.intermediate_size, bias=False)
        self.up_proj = nn.Linear(self.hidden_size, self.intermediate_size, bias=False)
        self.down_proj = nn.Linear(self.intermediate_size, self.hidden_size, bias=False)
        self.act_fn = ACT2FN[config.hidden_act]

    def forward(self, x):
        down_proj = self.down_proj(self.act_fn(self.gate_proj(x)) * self.up_proj(x))
        return down_proj

Gating函数的计算和以往没有区别，还是以整个Batch来算softmax，但是计算精度上采用了FP32。此外，在做TopK和归一化选择前，进行了MoE Group的计算，总共分成了8个Group。topk选择的group为3个。然后对每个Group求最大的Softmax作为Group的scores，再从这里面选择出来 M 个Group。

class MoEGate(nn.Module):
    def __init__(self, config):
        super().__init__()
        self.config = config
        self.top_k = config.num_experts_per_tok
        self.n_routed_experts = config.n_routed_experts
        self.routed_scaling_factor = config.routed_scaling_factor
        self.scoring_func = config.scoring_func
        self.alpha = config.aux_loss_alpha
        self.seq_aux = config.seq_aux
        self.topk_method = config.topk_method
        self.n_group = config.n_group
        self.topk_group = config.topk_group

        # topk selection algorithm
        self.norm_topk_prob = config.norm_topk_prob
        self.gating_dim = config.hidden_size
        self.weight = nn.Parameter(
            torch.empty((self.n_routed_experts, self.gating_dim))
        )
        self.reset_parameters()

    def reset_parameters(self) -> None:
        import torch.nn.init as init

        init.kaiming_uniform_(self.weight, a=math.sqrt(5))

    def forward(self, hidden_states):
        # 以整个batch计算
        bsz, seq_len, h = hidden_states.shape
        ### compute gating score
        hidden_states = hidden_states.view(-1, h)
        logits = F.linear(
            hidden_states.type(torch.float32), self.weight.type(torch.float32), None
        )
        # 计算精度采用了FP32
        if self.scoring_func == "softmax":
            scores = logits.softmax(dim=-1, dtype=torch.float32)
        else:
            raise NotImplementedError(
                f"insupportable scoring function for MoE gating: {self.scoring_func}"
            )

        ### select top-k experts
        if self.topk_method == "gready":
            topk_weight, topk_idx = torch.topk(
                scores, k=self.top_k, dim=-1, sorted=False
            )
        elif self.topk_method == "group_limited_greedy":
            # 基于每个Token分组组内最大的softmax作为Group scores
            group_scores = (
                scores.view(bsz * seq_len, self.n_group, -1).max(dim=-1).values
            )  # [n, n_group]
            # 选择M个Group
            group_idx = torch.topk(
                group_scores, k=self.topk_group, dim=-1, sorted=False
            )[
                1
            ]  # [n, top_k_group]
            # 然后构建Groupmask, mask后再选择TopK
            group_mask = torch.zeros_like(group_scores)  # [n, n_group]
            group_mask.scatter_(1, group_idx, 1)  # [n, n_group]
            score_mask = (
                group_mask.unsqueeze(-1)
                .expand(
                    bsz * seq_len, self.n_group, self.n_routed_experts // self.n_group
                )
                .reshape(bsz * seq_len, -1)
            )  # [n, e]
            tmp_scores = scores.masked_fill(~score_mask.bool(), 0.0)  # [n, e]
            # 在前面基础之上执行topK
            topk_weight, topk_idx = torch.topk(
                tmp_scores, k=self.top_k, dim=-1, sorted=False
            )

        ### norm gate to sum 1
        if self.top_k > 1 and self.norm_topk_prob:
            denominator = topk_weight.sum(dim=-1, keepdim=True) + 1e-20
            topk_weight = topk_weight / denominator
        else:
            topk_weight = topk_weight * self.routed_scaling_factor
        ### expert-level computation auxiliary loss
        if self.training and self.alpha > 0.0:
            scores_for_aux = scores
            aux_topk = self.top_k
            # always compute aux loss based on the naive greedy topk method
            topk_idx_for_aux_loss = topk_idx.view(bsz, -1)
            if self.seq_aux:
                scores_for_seq_aux = scores_for_aux.view(bsz, seq_len, -1)
                ce = torch.zeros(
                    bsz, self.n_routed_experts, device=hidden_states.device
                )
                ce.scatter_add_(
                    1,
                    topk_idx_for_aux_loss,
                    torch.ones(bsz, seq_len * aux_topk, device=hidden_states.device),
                ).div_(seq_len * aux_topk / self.n_routed_experts)
                aux_loss = (ce * scores_for_seq_aux.mean(dim=1)).sum(
                    dim=1
                ).mean() * self.alpha
            else:
                mask_ce = F.one_hot(
                    topk_idx_for_aux_loss.view(-1), num_classes=self.n_routed_experts
                )
                ce = mask_ce.float().mean(0)
                Pi = scores_for_aux.mean(0)
                fi = ce * self.n_routed_experts
                aux_loss = (Pi * fi).sum() * self.alpha
        else:
            aux_loss = None
        return topk_idx, topk_weight, aux_loss

AddAuxiliaryLoss是辅助损失，具体代码如下。

class AddAuxiliaryLoss(torch.autograd.Function):
    """
    The trick function of adding auxiliary (aux) loss,
    which includes the gradient of the aux loss during backpropagation.
    """

    @staticmethod
    def forward(ctx, x, loss):
        assert loss.numel() == 1
        ctx.dtype = loss.dtype
        ctx.required_aux_loss = loss.requires_grad
        return x

    @staticmethod
    def backward(ctx, grad_output):
        grad_loss = None
        if ctx.required_aux_loss:
            grad_loss = torch.ones(1, dtype=ctx.dtype, device=grad_output.device)
        return grad_output, grad_loss

0x04 DeepSeek V3

V3 在基本的MoE框架上，延续了细粒度专家（finer-grained experts）和共享专家（Shared Expert Isolation）的设计。在门控网络和负载均衡方面都做了些改进。

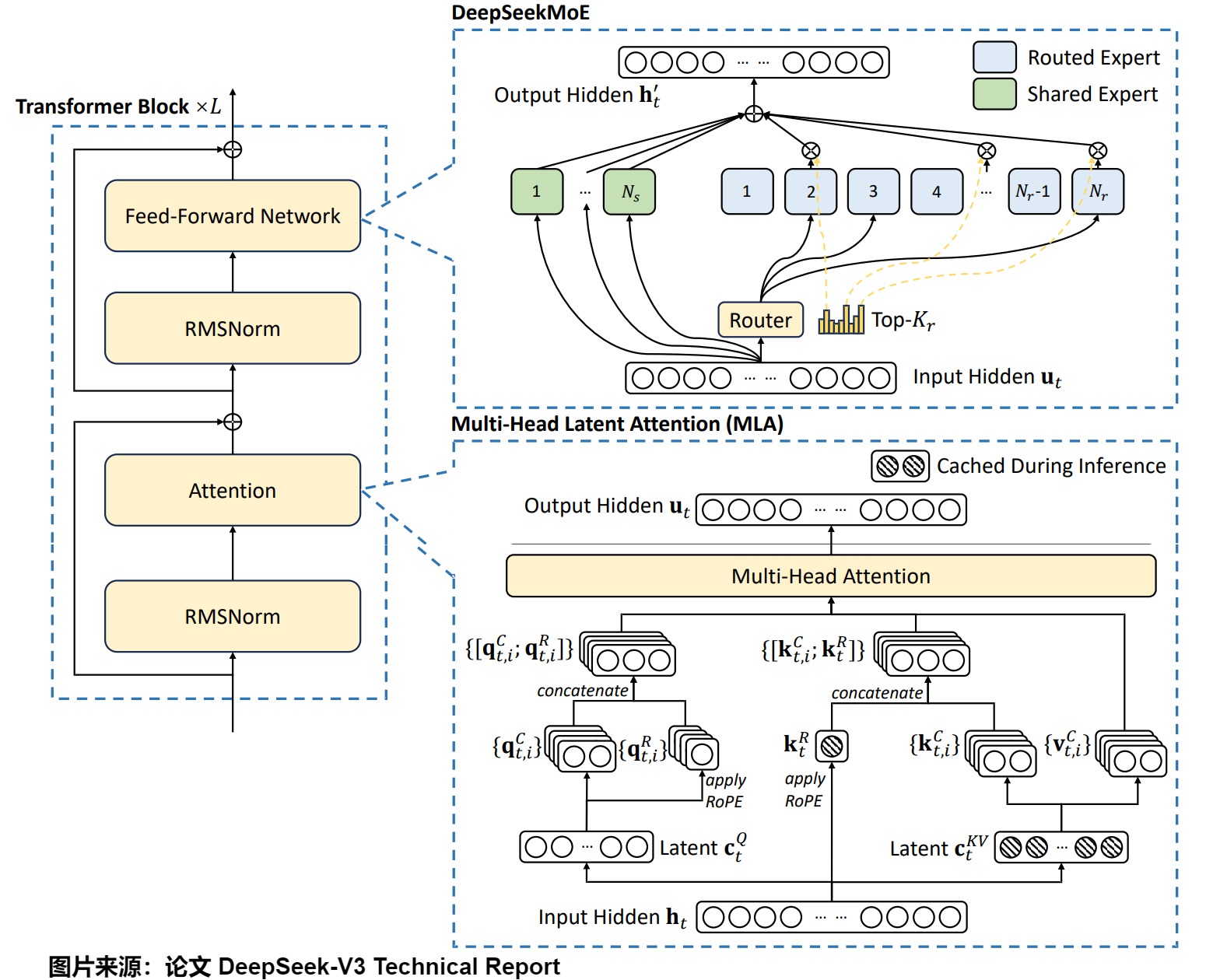
4.1 架构

下图是架构演进。可以看到，相对于前两版的计算框架，V3的主要修改还是门控网络的激活函数从 softmax 修改为 Sigmoid。另外，在Gating上还增加了bias。

4.1.1 Sigmoid

概念

Sigmoid函数的数学形式如下，其与累积分布函数（CDF）有相似之处。

$\sigma(x) = \frac{1}{1 + e^{-x}}$

其关键性质是：

输出范围：Sigmoid函数的输出值在0到1之间，可以看作是一个概率值。
平滑性：Sigmoid函数是一个平滑的、连续的函数，具有良好的导数性质。
非线性：Sigmoid函数是一种非线性函数，可以引入非线性变换，增加神经网络的表达能力。

对比

从实现门控的效果上看，Softmax和Sigmoid都能做实现筛选TopK的功能，也能做概率分布的归一化处理。但V3版的MoE为什么要做从Softmax到Sigmoid的升级？我们看看V3版相对于V2版的专家设置发生了哪些变化。

V2版。路由专家数：每个 MoE Layer 包含 162 个专家，其中 2 个是共享专家，160 个是路由专家，每个 Token 激活 2+6=8 个专家。共 236B 参数量，每个 Token 激活 21B 参数。
V3版。路由专家数： 256，激活专家数：8个，模型总参数671B，激活参数37B

可能原因如下：因为V3相对于V2的路由专家数增加了近100个，门控函数面对一个更大维度的操作。

当面对更多专家时，softmax函数会导致Gating Scores的区分度降低、计算误差加大，使得专家选择的误差很大。softmax要在内部对所有维度的值做归一化处理。因为所有维度加和要等于1，所以维度越大，每个维度值理论上分配的值就越小。而且DeepSeek-V2时已经采用了FP32的精度。这样在选取 TopK 个最大值时，对更小的小数位会更敏感，导致数据区分度不高，维度越大，问题越严重。
Sigmoid函数的值域更宽，更适合高维度操作。Sigmoid函数的是对每个专家分别计算一个 [0,1] 的打分，它并是不随专家维度变化而变化，理论上计算的打分值域更宽，区分度更高。
较大的 logits 值在 softmax 激活函数中会导致较大的梯度，这可能会引起训练不稳定。

另外，我们也可以从两个函数的梯度角度进行分析。

常见的负载均衡函数为：
$L_{aux} = <f,p> = \sum^n_{i=1}f_ip_i$
假设 $x_i$ 是logit， $p_i$ 是softmax的概率，则公式拓展为：
$L_{aux} = <f,p> = \sum^n_{i=1}f_ip_i = \sum^n_{i=1}f_i \cdot \frac{e^{x_i}}{\sum_j e^{x_j}}$
其梯度为：
$\frac{\partial L}{\partial x_k} = p_k(f_k - \sum_i f_ip_i)$
从梯度公式可以发现其特点：

如果 $p_k$ 为0，则梯度为0，就会停止更新梯度。
$ \sum_i f_ip_i$可以理解为按概率 𝑝 加权平均的 $f_i$ 。如果 $f_k$ 超过了平均值，那么 $x_k$ 会拿到一个正梯度，通过梯度下降会慢慢趋近于平均值，反之亦然。随着优化的深入， $f_k$ 的所有项都会逐渐趋于平均，也就满足了负载均衡。
softmax的加权平均结果是非常接近最大值的，导致次优值可能会拿到相反的梯度，这会带来一定的问题。

如果采用sigmoid并归一化，则有：
$p_i = \frac{\sigma(x_i)}{\sum_i \sigma(x_i)}$
按这个概率求出来的梯度形式为：
$\frac{\partial L}{\partial x_k} = p_k(1-\sigma_k)(f_k - \sum_i f_ip_i)$
其特点如下：

不仅是概率接近0，现在某个sigmoid接近1时，梯度也会消失。
括号内的部分，由于改成了sigmoid函数，不再有只拉低最高项的缺点了。

4.1.2 专家分组

DeepSeek-V3采用了专家分组，但是和Device-Limited Routing不同，V3主要是用于NVLINK和IB的带宽3.2x配比上。

4.2 负载均衡

下图给出了损失函数变化。

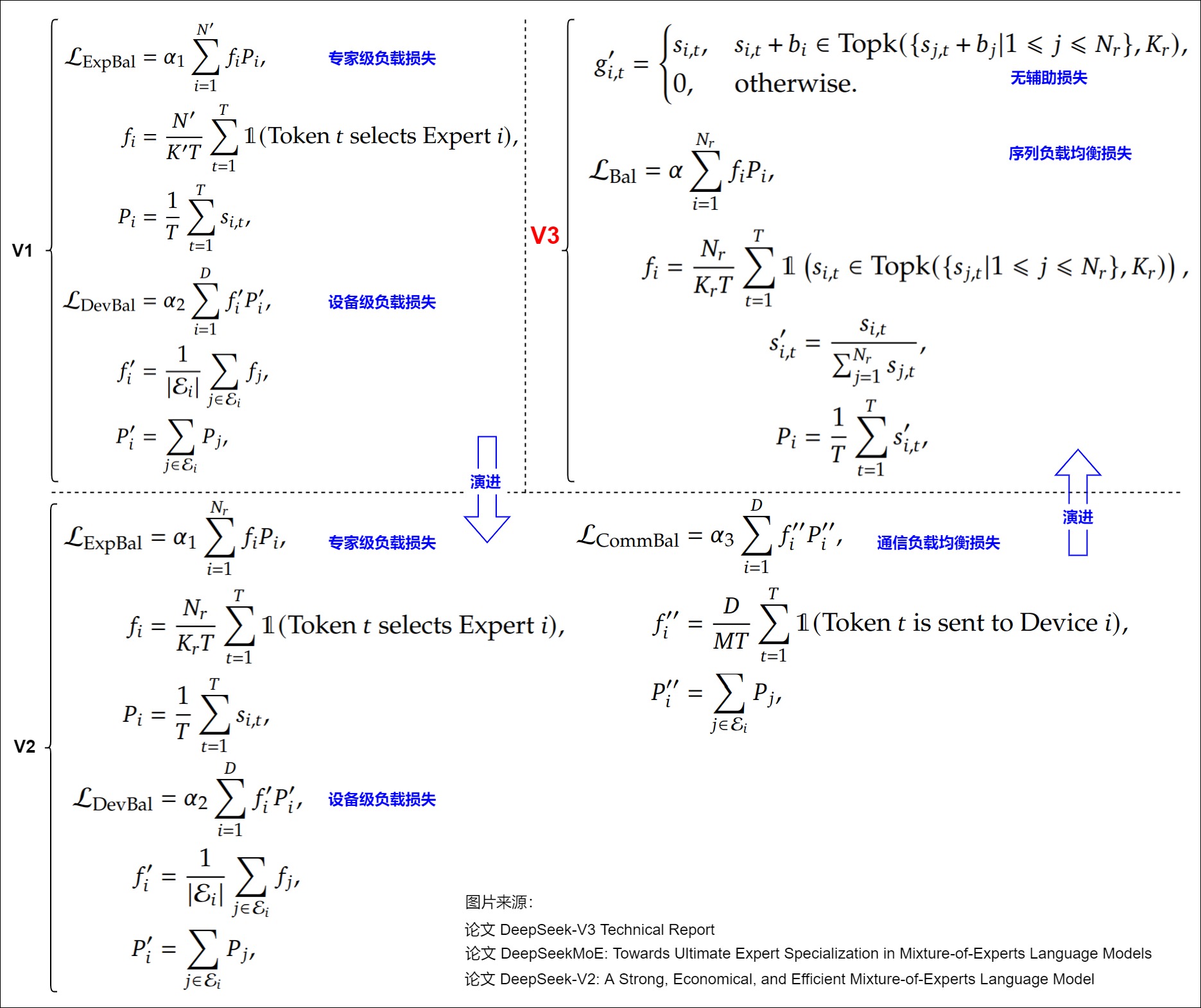
4.2.1 无辅助损失负载均衡

面对负载不均衡，Aux Loss的应对思路是通过额外的损失引导Router给出均衡的打分，而Auxiliary-Loss-Free Load Balancing的想法则是换个新的分配思路，即不改变Router现有打分结果，而是改变 $argtop_k\ p$ 这个分配方式。

DeepSeek在V1，V2版MoE模型中，增加了专家级，设备级和设备通信级等平衡负载辅助loss。这些辅助loss有几个问题：

只是为了做计算、通讯的负载均衡，对模型的效果调优并没有帮助。
难以调节权重，调低了无法促进均衡，调高了容易损害LM Loss。
甚至这些辅助loss增加过多，loss太大会对主模型造成影响，导致主模型的效果有损。

为了在负载均衡和模型性能之间实现更好的权衡，V3 采用了一种非常巧妙的无辅助损失的负载均衡策略（Auxiliary-Loss-Free Load Balancing），即把之前的各种辅助损失都去除，通过在Gating score中为每个专家增加了一个可动态调节的Bias项来做到负载均衡（这个偏置量仅仅用于topk筛选，不加入后续的权重计算）。

Bias方法具体如下。Bias仅用于路由计算，最终的weight还是采用原始的sigmoid(代码中的Original_score)。V2版选择专家是通过专家的门控权重 $𝑠_{i,𝑡}$ 来取 TopK ，V3版对每个专家维护一个可动态调节的bias。用专家的得分加上一个 bias 项来选择 Topk。向门控分数添加偏置项在概念上类似于直接对门控分数应用梯度更新，而不依赖于通过损失函数的反向传播。

bias的调节是通过一个偏置更新速度的超参数 𝛾 来完成。在训练过程中会持续监控每个batch的负载均衡情况。在每一个step结束时，会做如下操作。

如果某个专家负载过高，会将其对应的偏置项减少 𝛾，来降低门控权重，从而减少路由到该专家的token量。
如果某个专家负载不足，则会将其对应的偏置项增加 𝛾，来提升专家门控权重，从而增加路由到该专家的token量。

无辅助损失负载均衡如下图所示。使用辅助损失其实最终也是通过调整 $s_{i,t}$ 来最小化 $P_i$ 。如果我们可以直接调整 $s_{i,t}$ ，理论上我们应该能够实现与应用辅助损失类似的效果。

具体代码如下。首先获取分配给各专家的 token 数量平均值及所有专家的理论全局均值，然后计算给各专家分配的 token 数量与理论全局均值的差值，偏置项由该差值（或误差）的符号乘以固定更新率（fixed update rate）决定（该更新率为可调超参数）。

通过这种动态调整，DeepSeek-V3 在训练过程中保持了均衡的专家负载，并且相比仅通过纯辅助损失来促进负载均衡的模型，取得了更好的性能。

4.2.2 sequence粒度的负均衡损失

DeepSeek V3也增加了一个sequence粒度的负载均衡损失（Complementary Sequence-Wise Auxiliary Loss），为了防止单个序列内出现极端的不平衡，来平衡单个sequence的token分配给每个专家。

在上图中，T 是输入序列的总长度， $s'_{i,t}$ 代表归一化的输入序列和各个专家的亲和力， $P_i$ 代表第i个专家和序列内的每一个token的亲合度均值，代表了该专家和序列的整体亲合度， $f_i$ 代表第i个专家在该序列预测过程中的选中频率， $\alpha$ 为较小的常数超参数。可以看到， $f_iP_i$ 代表了第i个专家的负载强度，当部分专家反复在topk中被选中的时候， $L_{Bal}$ 会增大，即体现了对负载不均衡的惩罚。

与V1版的专家级辅助损失(Expert-Level Balance Loss)相比，Sequence-Wise的作用粒度不一样，Sequence-Wise的粒度是单条样本粒度的token做计算。Expert-Level Balance是一个Batch的多Sequence的token做计算。公式的计算形式并没有什么差异。

DeepSeekV3也强调，通过上面的策略，能达到一个非常好的负载均衡效果，所以在V3版并没有token-dropping策略。

4.2.3 路由

最后，在通信方面，DeepSeek-V3 使用限制路由机制来限制训练期间的通信成本，即每个token最多被发送到个算力节点，这些节点是根据分布在每个节点上的专家的最高 $\frac{K_r}{M}$ 个亲和力分数之和来选择的。在此约束下，deepseek v3的 MoE 训练框架几乎可以实现完全的计算-通信重叠。

4.3 vs Llama 4

我们来和 Llama 4 做一下比较。

在路由专家和共享专家上。Llama 4 Marverick MoE层使用128个路由专家和一个共享专家。每个token都会被发送到共享专家以及128个路由专家中的一个。

在部署位置上。

Llama 4 Scout 是MoE和MLP交替出现。实际上Google Switch Transformer，其论文中有提到“with experts at every other feed-forward layer”。另外，Google GLaM也是类似操作（每隔若干层有一个MoE）。Google ST-MoE 提供了更多的选择，比如：只有前几层是 MoE；只有中间几层是 MoE；Dense Transformer Layer 中交替插入 MoE；只有最后几层是 MoE。这或者是对训练稳定性与计算效率的一种妥协。
DeepSeek-V3 是前3层Dense MLP，后续全部为MoE。为何如何设置？在论文“DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models”中提到：第一层的负载均衡状态收敛很慢，因此保留第一层为 Dense Layer。这样的原因可能是：前几层更多关注低级且通用的特征，这些特征不太需要复杂的 MoE 机制，或者 MoE 中很难保持负载均衡。

Llama 4 的代码如下：

class MoEArgs(BaseModel):
    num_experts: int = -1
    capacity_factor: float = 1.0  # capacity factor determines how many tokens each expert can choose
    auto_scale_F: bool = (  # noqa: N815
        True  # if true, rescales hidden_dim such that number of activated params is same as equivalent dense layer
    )
    top_k: int = 1
    interleave_moe_layer_step: int = 1 # 表示每多少层有一个 MoE 层。

class TransformerBlock(nn.Module):
    def __init__(self, layer_id: int, args: ModelArgs):
        super().__init__()
        self.n_heads = args.n_heads
        self.dim = args.dim
        self.head_dim = args.dim // args.n_heads if args.head_dim is None else args.head_dim

        self.is_nope_layer = args.nope_layer_interval is not None and (layer_id + 1) % args.nope_layer_interval == 0

        use_rope = not self.is_nope_layer
        use_qk_norm = args.use_qk_norm and not self.is_nope_layer

        self.attention = Attention(args, use_rope=use_rope, use_qk_norm=use_qk_norm)

        if args.moe_args and (layer_id + 1) % args.moe_args.interleave_moe_layer_step == 0:
            self.feed_forward = MoE( # 设置MoE
                dim=args.dim,
                hidden_dim=int(args.ffn_exp * args.dim),
                ffn_dim_multiplier=args.ffn_dim_multiplier,
                multiple_of=args.multiple_of,
                moe_args=args.moe_args,
            )
        else:
            hidden_dim = int(4 * args.dim)
            hidden_dim = int(2 * hidden_dim / 3)
            if args.ffn_dim_multiplier is not None:
                hidden_dim = int(args.ffn_dim_multiplier * hidden_dim)
            hidden_dim = args.multiple_of * ((hidden_dim + args.multiple_of - 1) // args.multiple_of)

            self.feed_forward = FeedForward(
                dim=args.dim,
                hidden_dim=hidden_dim,
            )
        self.layer_id = layer_id
        self.attention_norm = RMSNorm(args.dim, eps=args.norm_eps)
        self.ffn_norm = RMSNorm(args.dim, eps=args.norm_eps)

        self._register_load_state_dict_pre_hook(self.load_hook)

4.4 实现

671B模型的相关配置如下

{
    "vocab_size": 129280,
    "dim": 7168,
    "inter_dim": 18432,
    "moe_inter_dim": 2048,
    "n_layers": 61,
    "n_dense_layers": 3,
    "n_heads": 128,
    "n_routed_experts": 256,
    "n_shared_experts": 1,
    "n_activated_experts": 8,
    "n_expert_groups": 8,
    "n_limited_groups": 4,
    "route_scale": 2.5,
    "score_func": "sigmoid",
    "q_lora_rank": 1536,
    "kv_lora_rank": 512,
    "qk_nope_head_dim": 128,
    "qk_rope_head_dim": 64,
    "v_head_dim": 128,
    "dtype": "fp8"
}

模型结构如下：

DeepseekV2MoE(
  (experts): ModuleList(
    (0-63): 64 x DeepseekV2MLP(
      (gate_proj): Linear(in_features=2048, out_features=1408, bias=False)
      (up_proj): Linear(in_features=2048, out_features=1408, bias=False)
      (down_proj): Linear(in_features=1408, out_features=2048, bias=False)
      (act_fn): SiLU()
    )
  )
  (gate): MoEGate()
  (shared_experts): DeepseekV2MLP(
    (gate_proj): Linear(in_features=2048, out_features=2816, bias=False)
    (up_proj): Linear(in_features=2048, out_features=2816, bias=False)
    (down_proj): Linear(in_features=2816, out_features=2048, bias=False)
    (act_fn): SiLU()
  )
)

MoE的代码如下：

class MoE(nn.Module):
    def __init__(self, args: ModelArgs):
        super().__init__()
        self.dim = args.dim
        assert args.n_routed_experts % world_size == 0
        self.n_routed_experts = args.n_routed_experts # 路由专家个数
        self.n_local_experts = args.n_routed_experts // world_size
        self.n_activated_experts = args.n_activated_experts # 激活专家个数
        # 计算本地所要创建的Expert
        self.experts_start_idx = rank * self.n_local_experts
        self.experts_end_idx = self.experts_start_idx + self.n_local_experts
        self.gate = Gate(args) # 门控函数
        # 本地专家只创建根据world size和Rank计算出来的一个区间
        self.experts = nn.ModuleList([Expert(args.dim, args.moe_inter_dim) if self.experts_start_idx <= i < self.experts_end_idx else None
                                      for i in range(self.n_routed_experts)])
        # 共享专家列表其实就是一个MLP，MLP的维度依据共享专家的个数来进行扩大
        self.shared_experts = MLP(args.dim, args.n_shared_experts * args.moe_inter_dim)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        shape = x.size()
        # 将一个Batch的输入全部展平
        x = x.view(-1, self.dim)
        weights, indices = self.gate(x) # 选取哪些专家以其权重
        y = torch.zeros_like(x) # 初始化结果矩阵
        # bincount()函数统计非负整数张量中每个值出现的次数，这里是统计在所有batch中每个专家被选中了多少次
        counts = torch.bincount(indices.flatten(), minlength=self.n_routed_experts).tolist()
        # 仅计算了Local Expert, 应该是推理阶段的代码, 训练dispatch没有实现。循环的维度是专家
        for i in range(self.experts_start_idx, self.experts_end_idx):
            if counts[i] == 0:
                continue # 在所有batch的数据中，这个专家都没有被选择，就跳过
            expert = self.experts[i]
            # where()函数会依据给定的条件对张量元素进行选择性操作，返回满足条件元素的索引（行和列）。这里i是专家的id，所以是得到在分发给这个专家的所有token的索引
            idx, top = torch.where(indices == i)
            y[idx] += expert(x[idx]) * weights[idx, top, None]
        # 共享专家的输出直接添加到y中
        z = self.shared_experts(x)
        # 结果是会combine做allreduce的
        if world_size > 1:
            dist.all_reduce(y)
        return (y + z).view(shape)

门控函数的实现如下。

class Gate(nn.Module):
    def __init__(self, args: ModelArgs):
        super().__init__()
        self.dim = args.dim
        self.topk = args.n_activated_experts
        self.n_groups = args.n_expert_groups # 一共几组
        self.topk_groups = args.n_limited_groups # 选择几组
        self.score_func = args.score_func
        self.route_scale = args.route_scale # 增加了一个route-scale=2.5放大系数
        self.weight = nn.Parameter(torch.empty(args.n_routed_experts, args.dim))
        # 671B模型的维度是7168, 增加了Bias项
        # 把每个专家的 bias 设置成了一个可学习的参数。跟论文中描述的增加和减少固定的 𝛾 量不一样。
        self.bias = nn.Parameter(torch.empty(args.n_routed_experts)) if self.dim == 7168 else None

    def forward(self, x: torch.Tensor) -> Tuple[torch.Tensor, torch.Tensor]:
        # 计算分数，使用输入张量与权重参数进行线性变换，以便选择topk
        scores = linear(x, self.weight)
        # 根据评分函数选择，应用softmax或sigmoid对分数进行归一化处理。
        if self.score_func == "softmax":
            scores = scores.softmax(dim=-1, dtype=torch.float32)
        else:
            scores = scores.sigmoid()
        # 保留了一份score用于Weight计算的不带Bias
        original_scores = scores
        # 如果存在偏置项，将其加到分数上
        if self.bias is not None:
            # 在671B模型中还添加了Bias, 这个和负载均衡相关
            scores = scores + self.bias
        if self.n_groups > 1:
            scores = scores.view(x.size(0), self.n_groups, -1) # 将分数进行分组
            if self.bias is None:
                group_scores = scores.amax(dim=-1)
            else:
                group_scores = scores.topk(2, dim=-1)[0].sum(dim=-1) # 每组选择最大两个得分进行求和，作为每组的代表得分
            # 找到前k组得分的索引，得到分数最高的topk_groups组
            indices = group_scores.topk(self.topk_groups, dim=-1)[1]
            # 没有选择的组被屏蔽
            mask = torch.zeros_like(scores[..., 0]).scatter_(1, indices, True)
            scores = (scores * mask.unsqueeze(-1)).flatten(1)
        # 从剩下的专家中，在每个输入上选择topk个专家的索引    
        indices = torch.topk(scores, self.topk, dim=-1)[1]
        # 从原始分数中依据索引indices来获取相应选中专家的权重, bias仅用于路由选择
        weights = original_scores.gather(1, indices)
        # 对weight归一化处理并增加了一个route-scale=2.5放大系数
        if self.score_func == "sigmoid":
            weights /= weights.sum(dim=-1, keepdim=True)
        # 使用权重缩放因子    
        weights *= self.route_scale
        return weights.type_as(x), indices

专家的实现如下。

class Expert(nn.Module):
    def __init__(self, dim: int, inter_dim: int):
        super().__init__()
        self.w1 = Linear(dim, inter_dim)
        self.w2 = Linear(inter_dim, dim)
        self.w3 = Linear(dim, inter_dim)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        return self.w2(F.silu(self.w1(x)) * self.w3(x))

0x05 其它探索

下面我们介绍一些与MoE有关联的探索。

5.1 MOA

尽管MoE研究主要集中在Transformer架构中的FFN层，也有研究人员提出了将 Attention Head 作为专家，相应的称为 Mixtrue of Attention Head（MoA）。其核心思想和 MoE 一样，原始的 Transformer 中每个 Token 都会经过所有的 Attention Head，而 MoA 在 Attention Head 之前添加一个 Top-K Router，每个 Token 只用经过部分 Token 即可。通过将多头注意力层与MoE结合，可以进一步提高性能并限制计算成本。

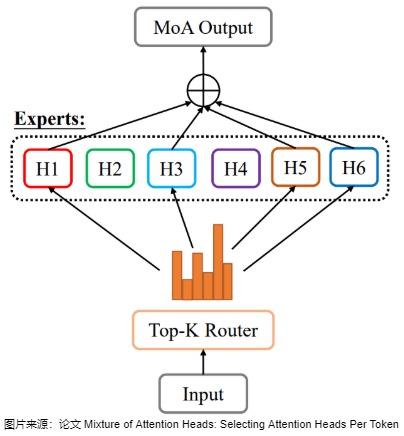
如下图所示，MoA采用两组专家，一组用于查询投影，另一组用于输出投影，它们通过一个共同的门控网络选择相同的专家索引。为了降低计算复杂度，MoA在注意力专家之间共享 $W_k$ 和 $W_v$ 投影权重，专家仅通过各自的查询 $q_t W_q$ 和输出 $o_iW_o$ 投影权重进行区分，从而允许预先计算 $KW_k$ 和 $VW_v$ 序列。

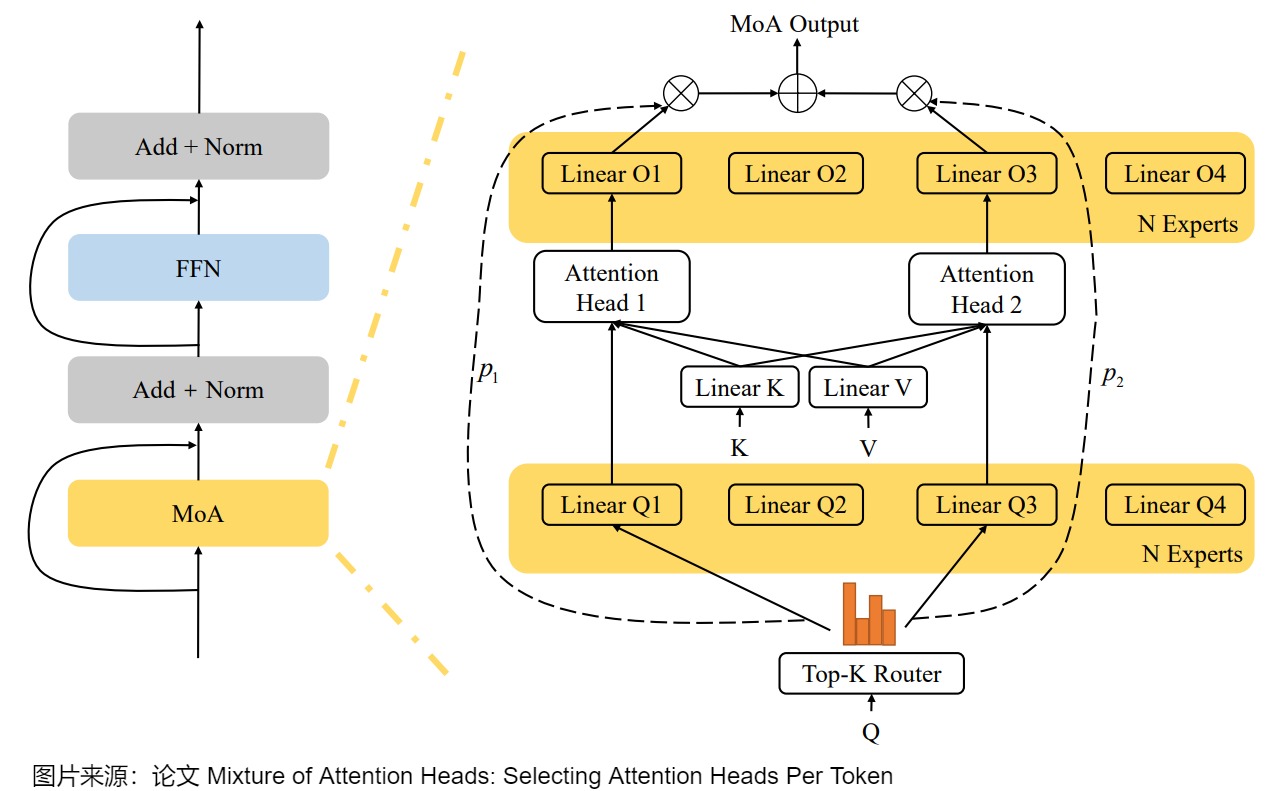
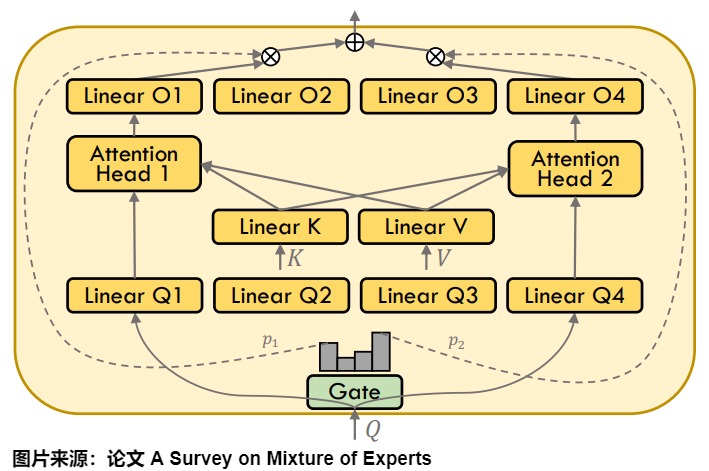
此外，MoA 和如下图所示的 MQA（Multi Query Attention）和 GQA（Grouped Query Attention）是兼容的。

5.2 MoD

5.2.1 概要

深度混合（MoD）是一种非常新的条件计算方法。MoD不是划分模型的深度，而是专注于让模型有能力决定每个输入的专用计算。它与 MoE 正交，因为它们不是互相替代，而是互补的技术，可以实现更高效和可扩展的推理。

在基于 Transformer 的语言模型中，模型为序列中的 Token 分配了几乎相同的计算 FLOP。在 LLM 的处理中，序列中的 Token 其实是有难易之分的，有些 Token 需要使用比较多的计算资源，而有些 Token 比较简单，实际并不需要同样的计算资源，这也就导致存在计算浪费。

MoD作者提出了在模型中的不同位置动态分配 FLOP 的方案。具体来说，在一个 Transformer Block 中，使用一个 Router 模块来控制该层参与计算的 Token（Top-K），而其他 Token 通过残差连接的方式直接输入到下一个 Transformer Block 中。由于 Top-K 超参是先验确定的，因此可以保证该过程中的张量大小都是确定的，也就是静态计算图，相应的总的计算 Budget 也是完全可预测的，与此同时，Token 维度又是动态的，并且是上下文相关的。基于该方法训练的模型可以与等效 FLOPS 和训练时间的基线模型性能相当，而在推理时获得 50% 以上的速度提升。

5.2.2 思路

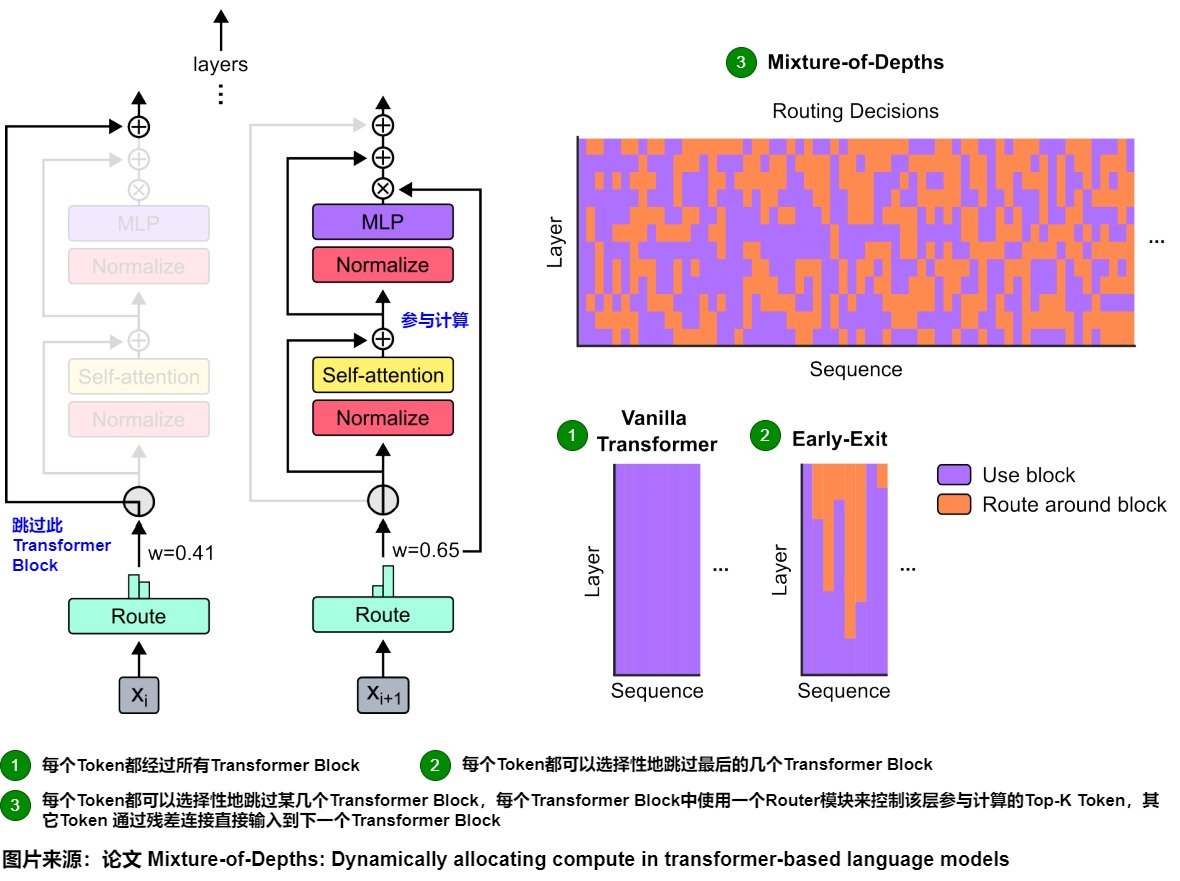
下图右侧给出了三种策略的区别。

Vanilla Transformer：每个 Token 都要经过所有的 Transformer Block。
Early-Exit：每个 Token 都可以选择性地跳过最后的几个连续的串行 Transformer Block。
Mixture-of-Depths：每个 Token 都可以选择性地跳过某几个（稀疏） Transformer Block。

下图左侧给出了MoD的思路。在每个 Transformer Block 前有一个 Router 模块来在潜在的计算路径中进行选择。但与MoE Transformer 不同，MoD 中的每个 Token 有两条计算路径，可以是左侧的通过残差连接直接连接到下一层，或者是像原始的 Transformer 一样经过 Self-Attention + MLP。

Router 模块对于每个 Token 都会输出一个标量，比如针对 Xi 输出 w=0.41，表示 Xi不走当前 Block，针对 Xi+1 输出 w=0.65，表示Xi+1要走当前 Block。而在 MoE 中，如果有 N 个专家，则每个 Token 都有 N 个计算路径（忽略丢弃的情况）。如果 MoD 中的 Top-K 大小与最大序列长度相同，则退化为原始的 Transformer，每个 Token 都要经过所有 Block。

5.2.3 Budget

作者同样利用了容量（Capacity）的概念来确定每个前向传递的总计算 Budget，它定义了给定计算输入的总 Token 数（例如，参与 Self-Attention 的 Token 数，MoE 中专家对应的 Token 数等）。

在 MoE 中，每个专家的大小和原始模型的 FFN 的大小相同，如果是 Top-1 Router，则总的计算量和原始 Transformer 模型相当。对于每个 Token 多个专家的情况，计算量会大于原始 Transformer 模型。对于静态图计算而言，一旦容量确定，相应的计算量也就确定。Token 不足则会 Padding，Token 过多则会丢弃，总的计算量不会因为 Router 的改变而变化。

对于 MoD 而言，通过降低容量可以实现比原始 Transformer 更低的计算需求。然而，随意使用较小的计算 Budget 可能导致性能的下降。

5.2.4 路由机制

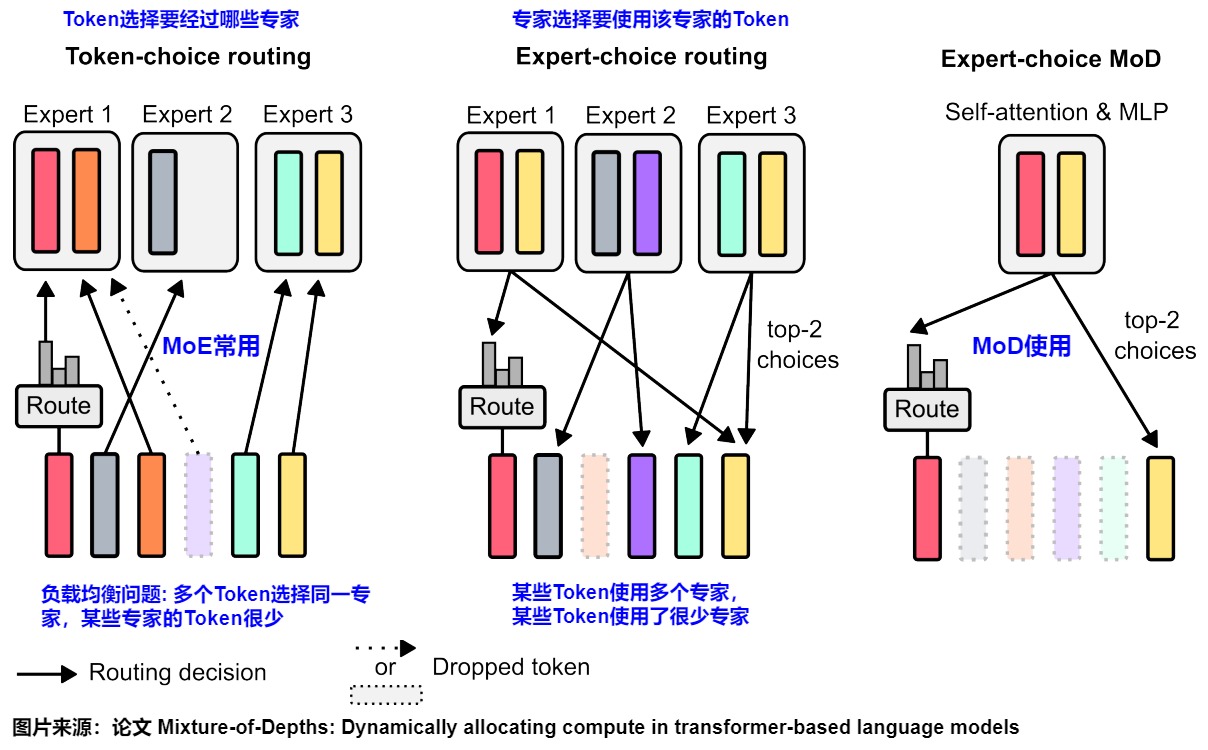
在 MoE 中通常会使用 Token-Choice 的方案，而在本文的 MoD 中作者选择了 Expert-Choice 的方案，如上图右所示，主要有 3 个优势：

不存在负载均衡问题，因此不需要像 Token-Choice 那样还要添加一个负载均衡损失。
MoD 中只有两个计算路径，每个 Token 只会走一个路径，Expert-Choice 的 Top-K 机制可以很容易实现这一点。
Token-Choice 的每个 Token 都是独立计算路由的，也就无法精准的控制 Budget。

5.2.5 采样

使用 Expert-Choice 有很多优势，但也有一个明显不足，Decoder-Only 的 LLM 是因果（Causal）模型，也就是每个 Token 都只依赖之前的 Token，而不依赖之后的 Token。而 Top-K 操作却是非因果的，要从一个序列中选择 Top-K 个 Token 需要知道整个 Token 序列，因此在推理阶段需要去掉 topk 操作（在训练阶段是可以知道整个序列的，因此可以只用 topk 来选择对应的 K 个 Token）。

为了解决这个问题，作者测试了两种方案：

增加二元交叉熵损失：每个 Token 都会输出一个 0-1 之间的标量值，大于 0.5 表示该 Token 在 Top-K 中，小于 0.5 则表示该 Token 不在 Top-K 中，此方案会影响原有的建模目标。该方案中 Router 输出 Logits，topk 操作（比如 torch.topk()）提供 Target。
增加一个小的 MLP 预测器：和 Router 有相同的输入，直接预测某个 Token 是否在 Top-K 中，这里会 Stop Gradient，也就是 MLP 预测器的梯度不会继续传播，因此不会影响建模目标。

需要说明的是，以上两种方法都无法保证选择的 Token 数一定是 Top-K 个，但可以非常接近，作者评估其可以获得 99% 左右的准确率。

5.2.6 路由讨论

我们再来分析下路由机制。

直观地说，一个token可能学会绕过某个计算单元（transformer block），因为在该步骤进行预测比较容易（通过辅助损失或者辅助预测器），但是路由网络学到的不仅仅是这个策略，如果一个token在某个计算单元中不参与自注意力层的计算，那么位于这个token后面的所有其他token也无法通过自注意力观察到这个token。这是因为自注意力机制允许每个token关注序列中的所有其他token，以捕捉这些token之间的依赖关系。但是如果一个token决定跳过某个transformer block的自注意力层的计算，那么位于这个token后面的所有token也无法通过自注意力机制关注这个token了。这也导致了MoD中路由决策的复杂性，因为一个token的路由决定会影响到其他token，所以路由机制需要考虑这些潜在的影响。如果路由网络决定让一个重要的token跳过计算，这可能会阻碍后面的token获取关键信息。因此路由网络需要学习平衡每个token的计算需求和对其他token的潜在影响，这使得路由决策变成了一个复杂的优化问题。

这一见解为MoD变体打开了大门。MoD可以用来解耦自注意力机制中的查询（query）、键（key）和值（value），我们可以设计MoD变体，为查询、键和值独立地机型路由决策。这意味着一个token可能在某个注意力头中被视为一个重要的查询，但在另一个注意力头中却不被是为一个重要的键。这种解耦可以让路由网络做出更细粒度的决策，更好地捕捉每个token在不同角色下的重要性。

作者进一步推测，有些token可能在上下文中具有重要的信息价值，即使它们在当前的查询步骤中并不重要。这些token可能携带了对理解整个序列或者完成任务至关重要的信息，然而在标准的Transformer中，如果这些token距离当前查询位置很远，则很难被有效利用。为了解决这个问题，作者提出可以使用路由机制来识别这些携带长期信息的token，路由网络可以将这些token引入一个特殊的长期记忆缓冲区，然后这个记忆缓冲区可以在未来的计算中被访问，即使那些token在原始序列中已经很远了，这使得模型能够更有效地捕捉和利用长距离的依赖关系。作者指出,这种长期记忆机制的一个优点是,对于每个token是否应该被加入长期记忆,可以在它第一次被处理(即"记忆编码"阶段)时就做出决定。这意味着,模型不需要在每个后续的查询步骤中都重新评估每个token的长期重要性。

这些突出了自适应计算，特别是学习路由在改进语言模型的记忆和上下文处理能力方面的潜力，通过识别和存储携带长期信息的token，路由机制可以成为一种强大的工具，用于扩展模型的有效上下文长度，并更好地捕捉长距离依赖。

5.3 MoE 与大型多模态模型的结合

论文“ MoE-LLaVA: Mixture of Experts for Large Vision-Language Models” 将 MoE 与 LLaVA 结合，实现了效率与性能的平衡。

作者提出了一种新的 LMM 训练策略 MoE-tuning，可以将 MoE 模型引入到 LMM 中，在保持计算成本恒定的情况下，有效解决与多模态学习和模型稀疏性相关的性能下降问题。同时，提出 MoE-LLaVA 模型，将 LLaVA 中的 LLM 替换为 MoE 模型，可以在推理阶段通过 Router 仅激活 topk 个专家。实验表明，MoE-LLaVA 在视觉理解方面有卓越的性能，并可以有效减少幻觉现象。

整个训练分 3 个阶段完成：

第一阶段：只训练 MLP，其他参数保持冻结。
第二阶段：放开除了 Vision Encoder 之外的所有参数。
第三阶段：将 LLM 中的 FFN 扩展为 MoE，也就是将 FFN 扩展为 E 个 FFN 并行排列，然后在之前添加 Router 层。只训练 MoE 和 MLP 层。

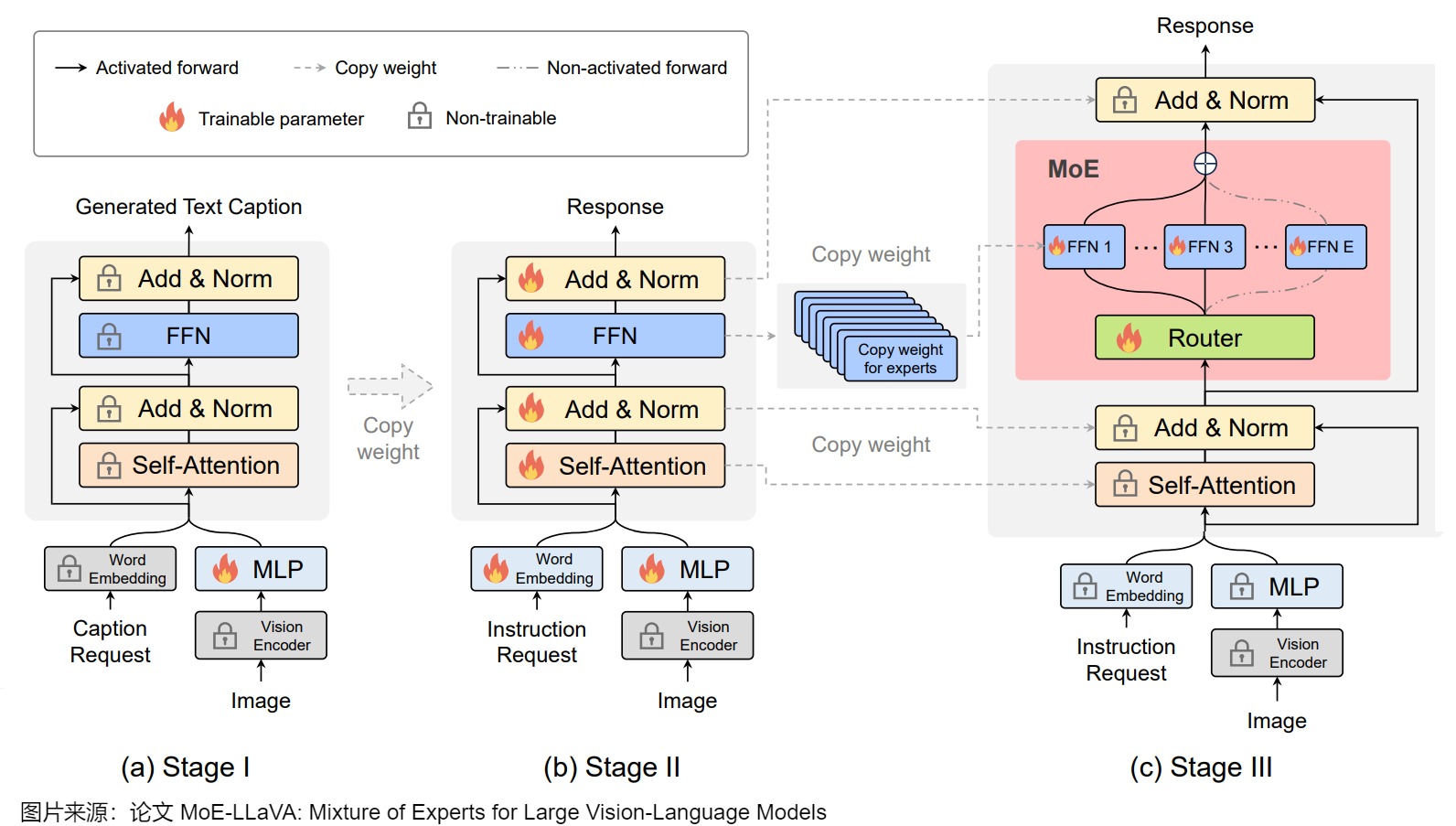
MoE中，Router 作用和传统的 MoE 一致，用于选择 topk 的 Expert（FFN）。除了自回归损失外，作者额外添加了一个 Laux 损失，其主要目的是实现各个 Expert 的负载均衡。

5.4 LoRA 与专家混合

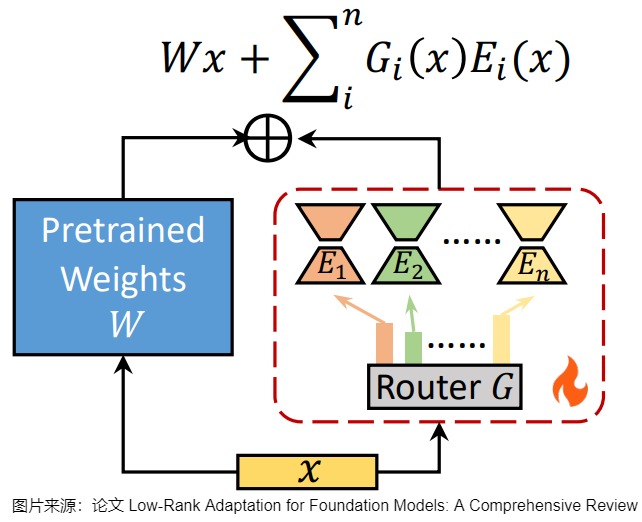
LoRA架构发展的一个重要分支就是将LoRA与MoE结合。该方案可以联合学习混合权重和LoRA插件，其中每个LoRA插件充当一个专家，而路由网络用来根据输入确定专家的权重或选择。在微调期间，预训练的 LLM 权重保持固定，而 LoRA 专家和路由器进行训练。LoRA专家的混合提供了一种机制，允许模型利用在不同任务上学到的知识，通过专家系统的方式进行有效的集成和泛化。

典型的框架如下图所示。

5.4.1 分类

基于 LoRA - MoE 方法的研究可大致分为三类，主要目标分别为：（1）提高性能和参数效率，（2）在微调期间保留知识，（3）适应多任务学习。虽然这些类别突出了不同的重点，但许多方法同时解决了多个目标。

下图给出了一些常见方案的比较。

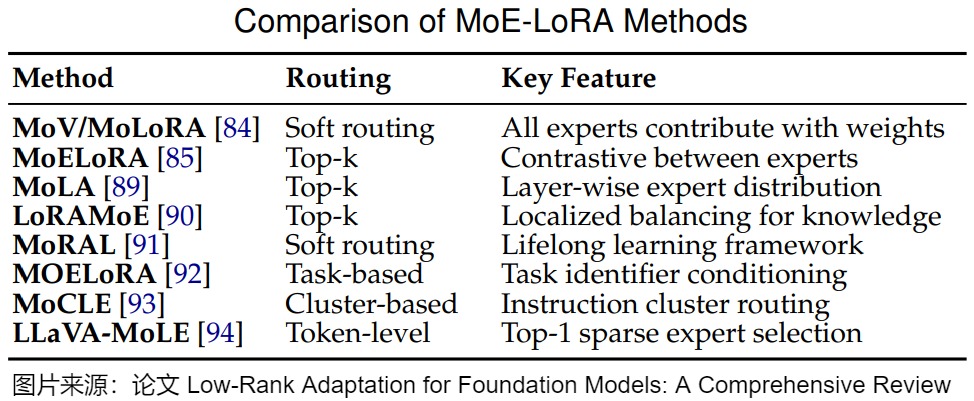
效率导向设计

此类方法旨在以最小的参数开销实现与全量微调相当的性能。

MoV 和 MoLoRA，旨在在更新不到 1%的参数的情况下实现全量微调性能，并提高对未见过任务的泛化能力。MoV 和 MoLoRA 分别使用向量和 LoRA 适配器作为专家，并采用软合并策略，其中所有专家根据路由器概率对输出做出贡献。
MoELoRA，将 LoRA 模块视为 MoE 框架内的专家。MoELoRA 包含多个 LoRA 专家和一个门控网络，用于路由和负载平衡，以防止收敛到有限的专家集。在专家之间应用对比学习缓解了 MoE 模型中常见的随机路由问题。
然而，固定数量的 LoRA 专家（例如 MoELoRA）缺乏灵活性，并且由于表示崩溃或学习到的路由策略过拟合可能会变得冗余。为了解决这个问题，MoLA 提出了一种跨不同 Transformer 层灵活分配 LoRA 专家的层级专家分布方法。MoLA 采用 top - k 路由机制为每个输入选择相关专家。除了提高性能和参数效率外，MoLA 由于其稀疏专家激活而展示出有前途的持续学习能力，使模型能够在适应新领域的同时保留来自先前领域的知识。

基于记忆的适应

这些方法侧重于在适应过程中防止灾难性遗忘，解决了在将 LLM 适应到新任务或领域时知识保留的挑战。

LoRAMoE引入了多个通过路由器网络集成的 LoRA 专家，使用局部平衡约束鼓励一些专家专注于利用世界知识来进行下游任务。它采用 top - k 路由策略，使模型能够在提高多个任务性能的同时保持世界知识。
MoRAL使用来自非结构化文本的问答对，并将 MoE 的多任务处理能力与 LoRA 的参数效率相结合。它采用软路由机制，其中所有专家根据路由器概率对输出做出贡献。MoRAL 在适应新领域的同时保持对先前见过任务的性能，解决了灾难性遗忘问题。

基于任务的集成

这些方法解决了领域特异性和任务干扰挑战。领域特异性出现在基于通用数据训练的模型缺乏特定领域（如医学或金融）所需的专业知识时。任务干扰发生在多个任务及其数据集在训练期间竞争时，导致跨任务性能下降。

为了解决领域特异性问题，研究人员提出了很多方案。
- MOELoRA 可以用于多任务医学应用。MOELoRA 引入了多个 LoRA 专家，每个专家由低秩矩阵组成，具有基于任务身份控制每个专家贡献的任务驱动门控函数。这种方法允许特定任务的学习，同时在任务之间维护共享知识库。F
- MOA 是一种用于多任务学习的端到端参数高效调整方法。MOA 首先为不同任务训练单独的 LoRA 模块，然后使用基于域元数据的序列级路由机制将它们组合起来，允许灵活组合特定领域的 LoRA。
- XLoRA 采用深度层令牌级动态 MoE 策略。从预训练的 LoRA 适配器开始，XLoRA 使用利用隐藏状态的门控策略动态混合适应层。这使模型能够创建新颖的组合来解决任务，在科学应用中表现出强大的性能。
为了解决任务干扰问题，研究人员提出了很多方案。
- MoCLE 解决了视觉语言指令调整中的任务冲突。该方法引入了一种 MoE 架构，根据指令簇激活任务定制参数，采用簇条件路由策略并纳入一个通用专家以提高对新指令的泛化能力。
- LLaVAMoLE 可以减轻多模态 LLM 指令微调中的数据冲突。它引入了一种稀疏 MoE 设计，包含多个 LoRA 专家，并采用令牌级路由策略，其中每个令牌被路由到 top - 1 专家。这允许对来自不同领域的令牌进行自适应选择，有效地解决了数据冲突。
- HydraLoRA 是一种不对称的 LoRA 架构，其挑战了基于 MoE 的方法中的传统对称专家结构。通过实证分析，作者发现，在多任务设置中，来自不同 LoRA 头的矩阵参数趋于收敛，而矩阵参数保持不同。在此观察的基础上，HydraLoRA 引入了一种架构，其中所有任务共享矩阵，并具有多个特定任务的矩阵，采用可训练的 MoE 路由器自动识别训练数据中的内在组件。

通过采用各种路由策略和专家设计，这些方法能够有效地适应多个任务或领域，同时减轻干扰并保持特定任务的性能。LoRA 与 MoE 的集成在提高性能、保留知识和促进跨各种领域的多任务适应方面展示出了有前途的结果。

提升性能

现有方法从初始化、任务关系管理和效率等方面提升LoRA MoE的性能。

在初始化方面，Mixture-of-LoRAs首先分别训练多个LoRAs作为初始化，然后联合优化路由器和LoRAs。MultiLoRA 提出细化初始化以减少参数依赖，从而产生更平衡的单一子空间。
在任务平衡方面，MLoRE 在MoE结构中添加了一个低秩卷积路径以捕捉全局任务关系。MITLoRA 采用任务无关和任务特定的LoRA模块来解决任务冲突。
在效率方面，MoLA 自适应地为Transformer模型的不同层分配不同数量的LoRA专家以节省LoRA模块数量。LLaVA-MoLE 和SiRA利用稀疏计算来降低计算成本。此外，Octavius 通过实例级指令稀疏激活独立的LoRA专家以缓解任务干扰并提高效率。Fast LoRA 允许小批次中的每个样本拥有其独特的低秩适配器，实现高效的批处理。

此外，一些方法虽非明确基于MoE，但遵循MoE的理念。例如，I-LoRA 分别使用两个LoRAs来管理持续学习的长期和短期记忆。

5.4.2 LoRAMoE

我们以LoRMoE作为例子，看看如何将 LoRA 视为 MoE 的 “专家”。LoRAMoE 是通过 MoE-style 的插件集成多个 LoRA 作为专家，其目的是为了缓解大规模微调中的世界知识遗忘问题。

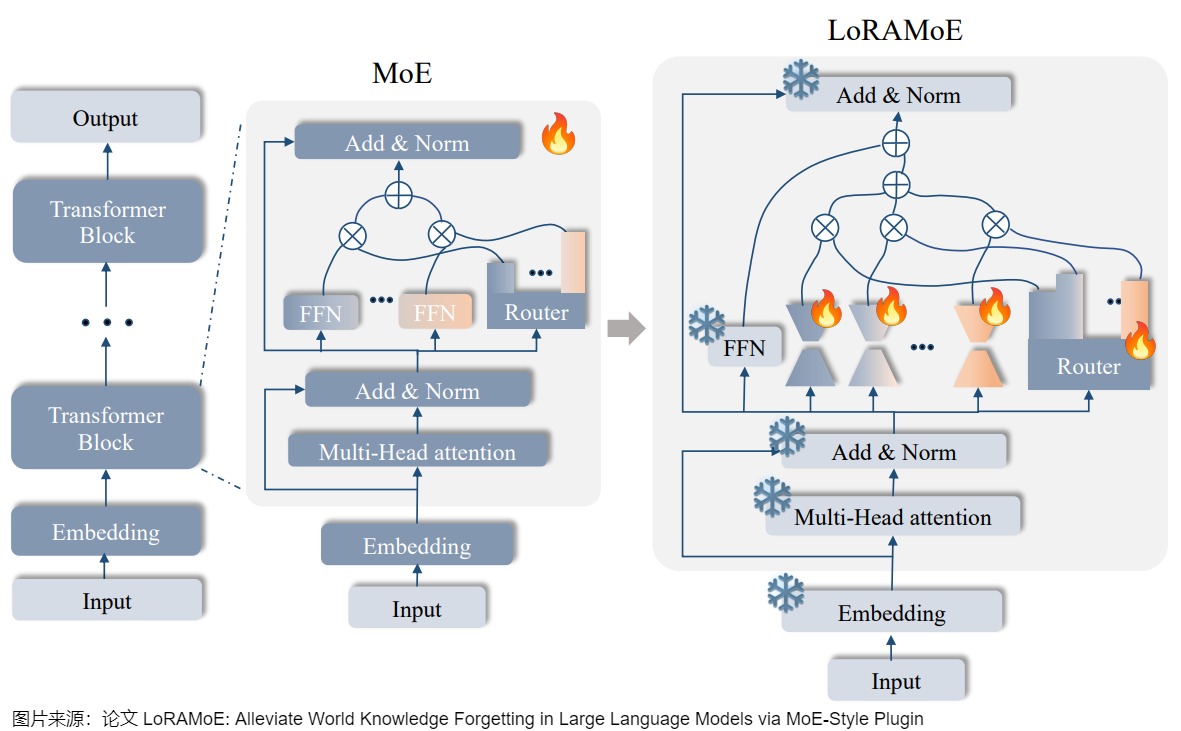
动机

作者发现，随着所用数据量的增长，SFT训练会导致模型参数大幅度偏离预训练参数，预训练阶段学习到的世界知识（world knowledge）逐渐被遗忘，虽然模型的指令跟随能力增强、在常见的测试集上性能增长，但需要这些世界知识的QA任务性能大幅度下降。

方案

作者提出的解决方案是：

数据部分：加入world knowledge的代表性数据集CBQA，减缓模型对世界知识的遗忘；
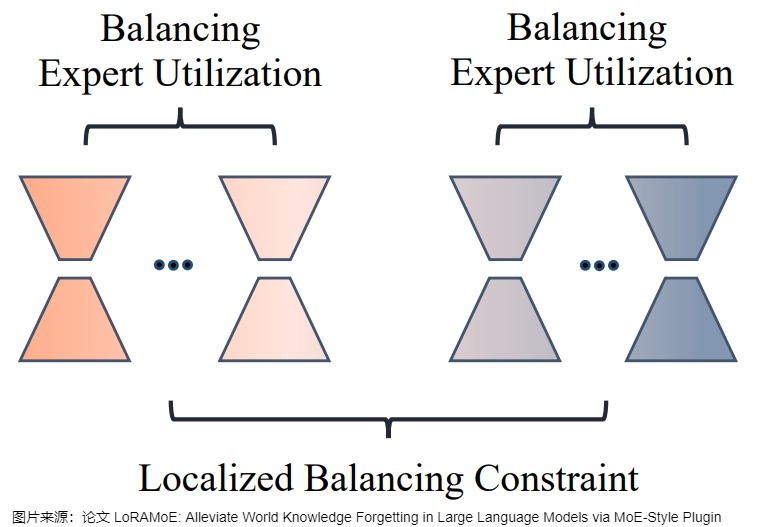
模型部分：以(1)减少模型参数变化；(2)隔离处理世界知识和新任务知识的参数为指导思想，设计了LoRAMoE方法，将LoRA专家们划分为两组，一组用于保留预训练参数就可以处理好的（和世界知识相关的）任务，一组用于学习SFT过程中见到的下游新任务，如下图所示。

训练

为了训练好这样的分组专家，让两组专家在组间各司其职（分别处理两类任务）、在组内均衡负载，作者设计了一种名为localized balancing contraint的负载均衡约束机制。具体地，假设Q为路由模块输出的重要性矩阵， $Q_{n,m}$ 代表第 n 个专家对第 m 个训练样本的权重， I 为作者定义的和 Q 形状相同的矩阵。负载均衡损失 $L_{lbc}$ 的定义为用 I 加权后的重要性矩阵 Z= I ∘ Q 的方差除以均值。

这样设计loss的用意是，对任意一种训练样本，两组LoRA专家组内的 𝐼 值是相等的，优化 $L_{lbc}$ 即降低组内路由权重的方差，使得组内负载均衡；两组专家之间，设专家组A对当前类型的数据更擅长，则其 I 值大于另一组专家B，训练起始阶段的A的激活权重就显著大于B，A对这种数据得到的训练机会更多，路由模块在训练过程中逐渐更倾向对这种数据选择A组的专家。这样一来，即使推理阶段没有数据类型 I 的信息，A对这种数据的路由值 Q 也会显著大于B的相应值，这就实现了两组专家各司其职的目标。

5.4.3 HydraLoRA

我们使用HydraLoRA 为例来进行学习，看看如何将 MoE 专家参数通过低秩分解进行压缩或者更好的优化。HydraLoRA 是一种新的参数高效微调架构，能够自动识别数据中的 “内在组件”—— 即子领域或不同任务，这些组件可能难以被领域专家明确界定。

HydraLoRA 的核心思想是通过共享的 A 矩阵和独立的 B 矩阵，最大限度地减少任务间的相互干扰，对每个内在组件进行优化调整。HydraLoRA 自主分配不同的 B 矩阵来捕捉特定任务的特性，而共享的 A 矩阵负责全局信息的整合，从而实现了高效的参数利用和性能提升。在复杂的多任务环境中，HydraLoRA 展现出了卓越的适应性，能够灵活处理各个内在组件，减少任务间的干扰并提高性能，显著提升模型的准确性和效率，同时优化了资源消耗。

动机

大型语言模型（LLMs）虽然在适应新任务方面取得了长足进步，但它们仍面临着巨大的计算资源消耗，尤其在复杂领域的表现往往不尽如人意。为了缓解这一问题，业界提出了多种参数高效微调（PEFT）方法，例如 LoRA。然而，LoRA 在面对复杂数据集时，总是难以与全参数微调的表现相媲美，尤其在处理更多样化或异质的训练语料库时，这一差距会进一步扩大。语料库的异质性意味着数据集的多样性，由于内容和风格各异，往往会引入干扰。PEFT 方法对此尤为敏感，在异构情况下性能损失更为严重。

为了突破这一瓶颈，来自澳门大学、德克萨斯大学奥斯汀分校以及剑桥大学的研究者联合提出了一种全新的非对称 LoRA 架构 —— HydraLoRA。与传统 LoRA 需要对所有任务使用相同的参数结构不同，HydraLoRA 引入了共享的 A 矩阵和多个独立的 B 矩阵，分别处理不同的任务，从而避免任务间的干扰。九头蛇（Hydra）的每个头就像 LoRA 中的 B 矩阵一样，专注于各自的特定任务，而共享的 A 矩阵则像九头蛇的身体，统一管理和协调，确保高效和一致性。无需额外工具或人为干预，HydraLoRA 能够自主识别数据中的隐含特性，极大提升了任务适应性与性能表现。借助这种多头灵活应对的机制，HydraLoRA 实现了参数效率与模型性能的双重突破。

观察

LoRA 的分析观察 1：在参数数量相同的情况下，与其对整个域数据集使用单个 LoRA，不如部署多个较小的 LoRA 模块，每个模块专注于特定的下游任务。此外，研究团队认为这种干扰并不限于显式的多任务训练场景。在任何训练设置中，这种干扰都有可能发生，因为所有数据集本质上都包含多个隐含的内在组件，例如子领域或域内的任务，这些组件甚至连领域专家也未必能够明确区分。
LoRA 的分析观察 2：当多个 LoRA 模块在不同数据上独立训练时，不同头的矩阵 A 参数高度相似，趋于一致，而矩阵 B 的参数则明显不同，易于区分。研究团队认为这种不对称现象主要源于 A 矩阵和 B 矩阵的初始化方式不同。A 矩阵倾向于捕捉跨领域的共性，而 B 矩阵则适应领域特定的差异。A 和 B 矩阵之间的区别为提升参数效率和有效性提供了重要见解。从效率角度来看，该研究假设 A 矩阵的参数可以在多个头部之间共享，从而减少冗余。就有效性而言，由于不同头部的 B 矩阵参数分散，说明使用单一头部来适应多个领域的效果可能不如为每个领域使用独立头部更为有效，因为这能最大程度地减少领域之间的干扰。

方案

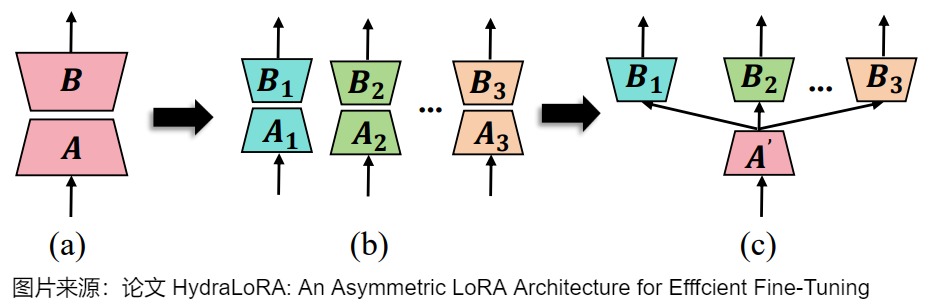
下图展示了HydraLoRA中LoRA架构变化。此图中仅显示了可调参数。

(a) 是LoRA架构，其中矩阵a用于实现低秩，矩阵B用于恢复。
(b) 在相同的参数计数下，单片LoRA被拆分为多个较小的a和b矩阵，以避免训练干扰。
© 基于(b) 进行演化，HydraLoRA具有共享a矩阵和多个b矩阵的不对称结构。通过引入多个 B 矩阵，HydraLoRA 能够有效区分数据中的内在组件，避免不同任务间的干扰。共享的 A 矩阵捕捉任务间的共性，不同的 B 矩阵处理任务的多样性，从而在多样化任务中实现更佳性能。显著提升了参数的使用效率。这种架构通过减少冗余，提升了计算和存储效率，尤其在大模型微调场景中表现突出。

训练&推理

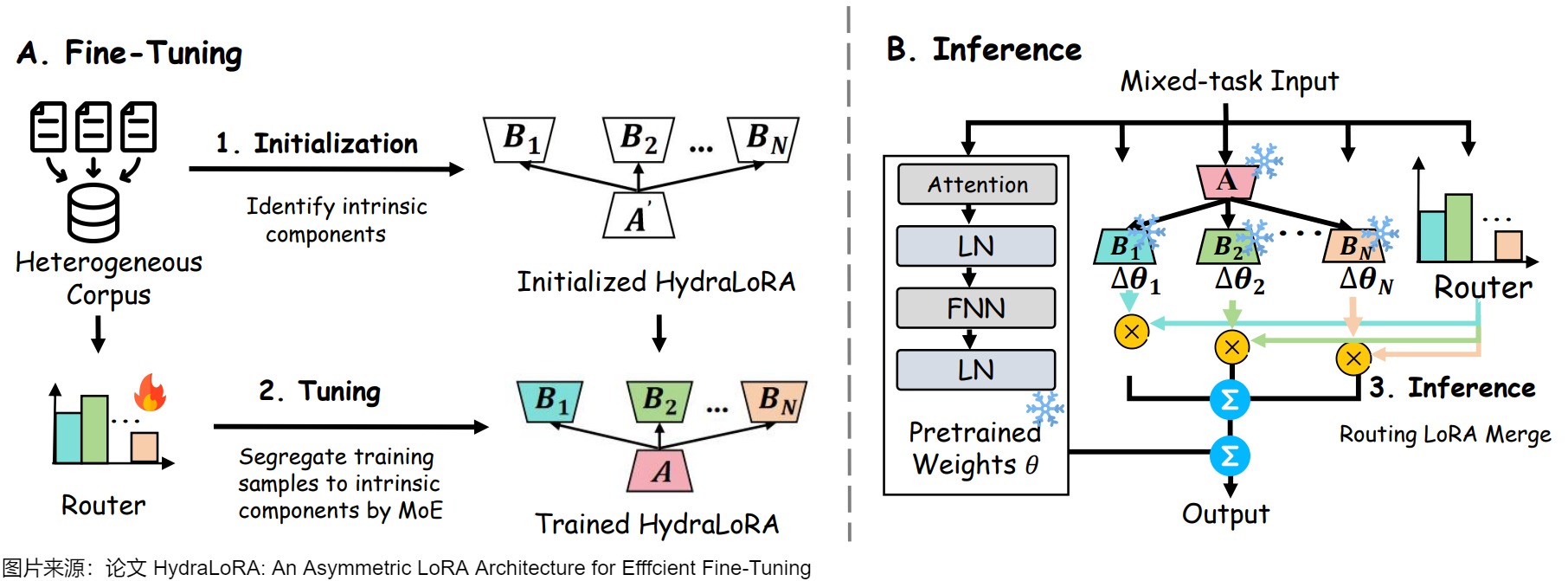
下图给出了训练和推理。

微调阶段：HydraLoRA 无需特定的领域知识即可自适应地识别并初始化 N 个内在组件。然后，它利用一个可训练的 MoE（Mixture of Experts）路由器，将每个内在组件视为专家，自动将训练样本划分到对应的组件进行微调。
推理阶段：HydraLoRA 通过训练完成的路由器，灵活且动态地合并多个 B 矩阵，以满足不同任务和数据的需求。这样的设计使得模型能够高效地适应多样化的应用场景，提升了整体性能和资源利用效率。

5.5 高效微调

我们来介绍下幻方 AI 最近发布的针对 MoE 模型的高效微调方案 ESFT。该论文是“Let the Expert Stick to His Last: Expert-Specialized Fine-Tuning for Sparse Architectural Large Language Models”。论文探索了基于 MoE LLM 的 PEFT 方法，研究内容主要包括 3 个方面：

研究特定任务中激活专家的离散度，并发现特定任务的路由分布高度集中，而激活专家在不同任务中又存在显著差异。
提出专家特化微调（Expert-Specialized Fine-Tuning，ESFT），该方面提高了微调效率，并且与全参数微调的性能相当甚至超过。
进一步分析了 MoE 架构对 ESFT 的影响。结果表明，具有细粒度专家的 MoE 模型在选择与下游任务最相关的专家组合方面更有利，从而提高了训练效率和训练效果。

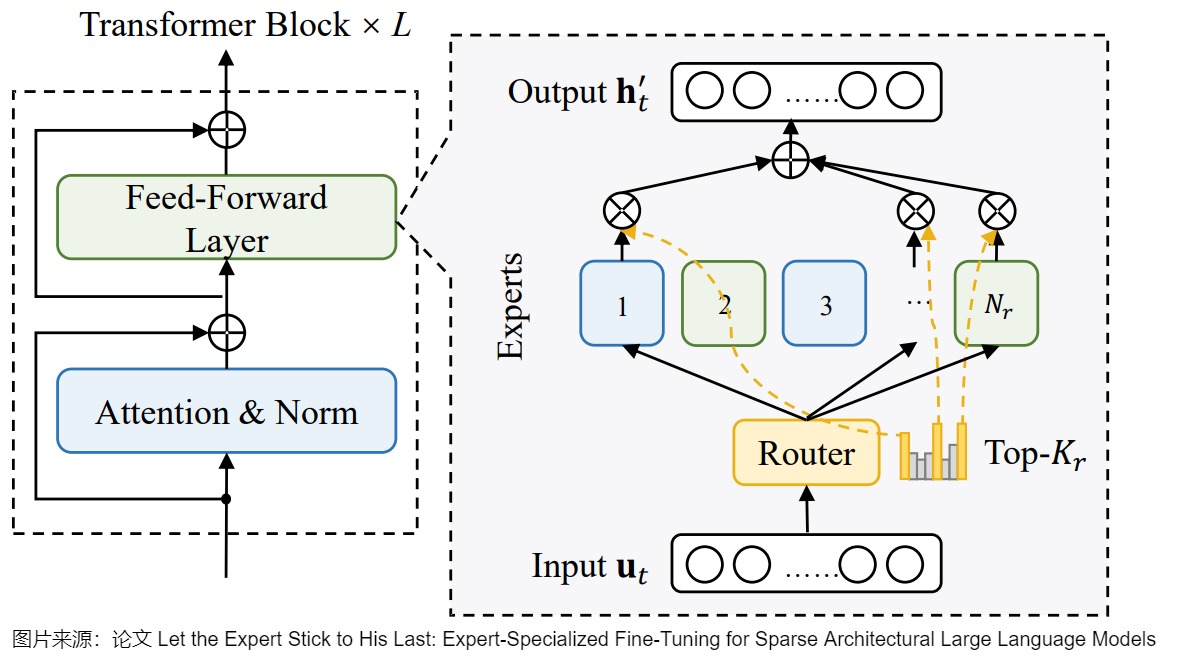
ESFT的核心思路如下图所示，在每个任务微调的时候都冻结大部分参数，比如 Attention 参数以及 MoE 中不相关的专家（蓝色），而只微调最相关的专家（绿色），并且这些专家都来自非共享专家。由于每个任务中最相关的专家比较少（不是固定数量，不同的任务数量不同），比如只有 6 个，因此整体可训练的参数也很少。

PS：需要说明的是，这里只微调最相关的专家并不意味着 Router 只会选择这些专家，其他专家依然会被路由到，只是说冻结的专家不会再进行梯度计算和参数更新，因此可以减少计算量。

论文没有用LoRA是因为作者想develop一种和MoE直接相关的方法。ESFT分为两个步骤：

任务分类：Task for Model Enhancement（Math/Code），能否通过专家微调的方式对它进行特殊优化；Task for Model Adaptation（比如一些客服的对话数据转换成summarization）。
确定专家：把任务输入进去后，看哪些专家被激活的最多，它就是我这个任务最需要的专家。在选择专家的时候，我们设计了Top-P：我们把每个模型的分数加起来，将概率归一化得到每个专家重要性的分布。如果选前K个专家，可以使得归一化之后的专家达到一个P值。选完专家之后，剩下的专家还要继续用（参与梯度传播，不参与梯度下降，也就是说不会被更新），不然模型的能力会大大降低。

ESFT中，我们发现专家存在分化的情况，不同的任务激活的专家是非常集中的。ESFT的优势在于可以在计算资源有限的情况下，提升模型的能力和泛化性。为什么ESFT比LoRA好？因为在LoRA中，每一个专家都会被训练。有时候专家不适应这个下游任务，为了满足loss，不擅长这个任务的专家也会被拿去做训练，这样在训练完之后反过来处理general任务的时候效果就会不好。但是ESFT本身就是先去选择专家，因此相比LoRA会有更强的泛化能力——让专业的人做专业的事。

大模型从Dense模型变成Sparse模型之后，如何微调那么多的参数？我们会找到一些适应这些任务的专家，微调这些专家而不是微调整个模型，这就需要在专家的角度做一些思考。

保持微调的专家是在训练之前就选择好的，并不是在训练中才去选择。具体来说，首选从任务数据集中选择 32 个 Sample，每个 Sample 的长度为 4096 个 Token，使用这 32 个 Sample 来挑选专家。

选择最相关的专家也有两种方式：

ESFT-Gate（Average Gate Score）：每个 Token 经过 Router 后都有对应 64 个专家的 Gate Score，将 2^17 个 Token 的 Gate Score 平均，然后挑选出分数最高的几个专家。
ESFT-Token（Token Selection Ratio）：使用每个专家被选中的 Token 的比例来选择最相关的专家。也就是将 2^17 个 Token 按 Router 分布在 64 个专家上，然后选择 Token 最多的几个专家。

0xEE 个人信息

★★★★★★关于生活和技术的思考★★★★★★

微信公众账号：罗西的思考

如果您想及时得到个人撰写文章的消息推送，或者想看看个人推荐的技术资料，敬请关注。

在这里插入图片描述

0xFF 参考

Noam Shazeer, Azalia Mirhoseini, Krzysztof Maziarz, Andy Davis, Quoc Le, Geoffrey Hinton, and Jeff Dean. 2017. Outrageously large neural networks: The sparsely-gated mixture-of-experts layer. arXiv preprint arXiv:1701.06538 (2017).

[1701.06538] Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer

[2006.16668] GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding

[2101.03961] Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity

[2103.13262] FastMoE: A Fast Mixture-of-Expert Training System

[2206.03382] Tutel: Adaptive Mixture-of-Experts at Scale

[2211.15841] MegaBlocks: Efficient Sparse Training with Mixture-of-Experts

[2305.13245] GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints

[2404.02258] Mixture-of-Depths: Dynamically allocating compute in transformer-based language models

A Survey on Inference Optimization Techniques for Mixture of Experts Models

A Survey on Mixture of Experts WEILIN CAI

Adaptive Mixtures of Local Experts

DeepEP Dispatch/Combine 图示 Marlene

「DeepSeek-V3 技术解析」：无辅助损失函数的负载均衡 Baihai IDP

「DeepSeek-V3 技术解析」：DeepSeekMoE Baihai IDP

Deepseek-MOE架构图解（V1->V2->V3）假如给我一只AI

DeepSeek-R1模型架构深度解读（三）弄懂DeepSeekMoE [AI算法之道](javascript:void(0)😉

DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model

DeepSeek-V3 Technical Report

DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models

DeepSeekV2之MLA(Multi-head Latent Attention)详解一滴水的使命

deepseek技术解读(3)-MoE的演进之路姜富春

Deepseek的MoE架构演变陈小小

DeepSpeed Inference全栈优化，延迟降低7.3倍，吞吐提升1.5倍 MLSys2024

DeepSpeed: Advancing MoE inference and training to power next-generation AI scale By DeepSpeed Team Andrey Proskurin , Corporate Vice President of Engineering

Googel最新MoD：动态计算资源分配，推理加速 50% AI闲谈

GPT-6的关键：混合体、混合专家和更高的数据质量 Tim在路上

GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding

HunYuan MoE：聊一聊 LLM 参数量、计算量和 MFU 等 AI闲谈稀疏层（Sparse Layers）

LLM MOE的进化之路，从普通简化 MOE，到 sparse moe，再到 deepseek 使用的 share_expert sparse moe chaofa用代码打点酱油

LLM 学习笔记-Deepspeed-MoE 论文 marsggbo

Mistral&LLama MoE:混合专家模型初探 JMXGODLZ

Mixtral 8x7B 详解异灵术好兄弟庞统

Mixtral of Experts

Mixtral of Experts笔记 Shane

Mixture of Parrots: Experts improve memorization more than reasoning

Mixture-of-Experts (MoE) 经典论文一览蝈蝈

MoE LLM对AI芯片通信的影响 TANG

MoE 系列论文解读：Gshard、FastMoE、Tutel、MegaBlocks 等 AI闲谈

MoE 训练到底是开 TP 还是 EP？ xffxff

MoE-LLaVA：MoE 与大型多模态模型的结合 AI闲谈 [AI闲谈](javascript:void(0)😉

MoEfication: Transformer Feed-forward Layers are Mixtures of Experts Zhengyan Zhang, Yankai Lin, Zhiyuan Liu, Peng Li, Maosong Sun, Jie Zhou

MOE介绍及其LLM方案整理假如给我一只AI

Moe已成为现阶段LLM的新标准 Tim在路上

MoE架构的“破局之路”：如何解决深度学习中的五大痛点 Alex [算法狗]

MoE模型的前世今生 Linsight

Moe模型的对比：Mixtral, Qwen2-MoE, DeepSeek-v3 Alex [算法狗]

OpenMoE笔记 Shane

OUTRAGEOUSLY LARGE NEURAL NETWORKS:THE SPARSELY-GATED MIXTURE-OF-EXPERTS LAYER

SwitchHead：使用专家混合模型注意力加速 Transformer

Z Tech｜前DeepSeek科学家万字大揭秘，RL与MoE如何点燃大模型革命 Z Potentials [Z Potentials](javascript:void(0)😉

【手撕LLM-sMoE】离GPT4又近了一步小冬瓜AIGC

【论文】混合专家模型（MoE）综述常华Andy [Andy730](javascript:void(0)😉

一文通透DeepSeek-V2(改造Transformer的中文模型)：详解MoE、GRPO、MLA v_JULY_v

专家混合模型（MOE）推理优化技术全景：从模型到硬件的深度解析北方的郎

从 GShard 到 DeepSeek-V3：回顾 MoE 大模型负载均衡策略演进小天狼星不来客

从条件计算到MoE：MoE的源起与发展（上篇）是海潮音

从条件计算到MoE：MoE的源起与发展（下篇）是海潮音

从零实现一个MOE（专家混合模型） KaiH

图解大模型训练系列之：DeepSpeed-Megatron MoE并行训练（原理篇）猛猿

图解大模型训练系列之：DeepSpeed-Megatron MoE并行训练（源码解读篇）猛猿

大模型KV Cache节省神器MLA学习笔记（包含推理时的矩阵吸收分析） BBuf

大模型LLM之混合专家模型MoE（下-实现篇）爱吃牛油果的璐璐

大模型中的MoE从入门到熟悉【分享】 Alex [算法狗]

大模型时代的数学基础(4) 扎波特的橡皮擦 [zartbot]

大模型时代的数学基础(5)-谈谈MoE和Mixtral 8x7B 扎波特的橡皮擦 [zartbot]@微信

大模型：混合专家模型（MoE）概述 [AI大模型前沿]

幻方AI ESFT：针对 MoE 的高效微调方案，媲美全参微调 AI闲谈 [AI闲谈](javascript:void(0)😉

浅读 DeepSeek-V2 技术报告 AGI 梦工厂

混合专家（MoE）的路由（Deepspeed ）杨歆

王文广揭秘MoE架构，万字长文解析GPT-4一直被模仿，从未被超越之谜——《秒懂大模型》走向未来 [走向未来](javascript:void(0)😉

用PyTorch从零开始编写DeepSeek-V2 Deephub

简单理解DeepSpeed-MoE专家模型和all2all通讯 voodoo

继续谈谈MLA以及DeepSeek-MoE和SnowFlake Dense-MoE 扎波特的橡皮擦 [zartbot](javascript:void(0)😉

详细谈谈DeepSeek MoE相关的技术发展渣B [zartbot](javascript:void(0)😉

香港科技大学发表的混合专家系统(MoE)综述无影寺

Adaptive Mixtures of Experts: https://www.cs.toronto.edu/~hinton/absps/jjnh91.pdf,

Adaptive Mixtures of Local Experts https://www.cs.toronto.edu/~hinton/absps/h91.pdf
Bertsekas, D.P. Auction algorithms for network flow problems: A tutorial introduction. Comput Optim Applic 1, 7–66 (.
https://doi.org/10.1007/BF00247653

Clark, Aidan, et al. “Unified scaling laws for routed language models.” International Conference on Machine Learning. PMLR, 2022.

Deepseek-V1 MoE: https://huggingface.co/deepseek-ai/deepseek-moe-16b-base/blob/main/modeling_deepseek.py

DeepSeek-V2 MoE: https://huggingface.co/deepseek-ai/DeepSeek-V2/blob/main/modeling_deepseek.py

DeepSeek-V3 MoE: https://github.com/deepseek-ai/DeepSeek-V3/blob/main/inference/model.py

DeepSeekMoE: Towards Ultimate Expert Specialization in Mixture-of-Experts Language Models https://arxiv.org/abs/1.06066

Eigen, David, Marc’Aurelio Ranzato, and Ilya Sutskever. “Learning factored representations in a deep mixture of experts.” v preprint arXiv:1312.4314 (2013).

Fedus, William, Barret Zoph, and Noam Shazeer. “Switch transformers: Scaling to trillion parameter models with simple and efficient sparsity.” The Journal of Machine Learning Research 23.1 (2022): 5232-5270.

Fuzhao Xue, Zian Zheng, Yao Fu, Jinjie Ni, Zangwei Zheng, Wangchunshu Zhou, and Yang You. 2024. Openmoe: An early effort on open mixture-of-experts language models. arXiv preprint arXiv:2402.01739 (2024).

GLaM: Efficient Scaling of Language Models with Mixture-of-Experts https://arxiv.org/abs/2.06905

GShard: Scaling Giant Models with Conditional Computation and Automatic Sharding: https://arxiv.org/pdf/2006.16668.pdf,
Hoffmann, Jordan, et al. “Training compute-optimal large language models.” arXiv preprint arXiv:2203.15556 (2022).

https://arxiv.org/pdf/2209.01667

https://github.com/withinmiaov/A-Survey-on-Mixture-of-Experts

https://huggingface.co/docs/transformers/v4.32.0/en/model_doc/switch_transformers

https://mp.weixin.qq.com/s/hI7q4_-ZMtFIQ-ckhM9_YQ

https://zhuanlan.zhihu.com/p/658007181

Introducing DBRX: A New State-of-the-Art Open LLM https://www.databricks.com/blog/roducing-dbrx-new-state-art-open-llm

Janus: A Unified Distributed Training Framework for Sparse Mixture-of-Experts Models: https://dl.acm.org/doi/pdf/10.1145/3269.3604869

Korthikanti, Vijay Anand, et al. “Reducing activation recomputation in large transformer models.” Proceedings of Machine ning and Systems 5 (2023).

Lepikhin, Dmitry, et al. “Gshard: Scaling giant models with conditional computation and automatic sharding.” arXiv int arXiv:2006.16668 (2020).

Lewis, Mike, et al. “Base layers: Simplifying training of large, sparse models.” International Conference on Machine ing. PMLR, 2021.

MegaBlocks: Efficient Sparse Training with Mixture-of-Experts: https://arxiv.org/abs/2211.15841,

Narayanan, Deepak, et al. “Efficient large-scale language model training on gpu clusters using megatron-lm.” Proceedings he International Conference for High Performance Computing, Networking, Storage and Analysis. 2021.

Outrageously large neural networks: The sparsely-gated mixture-of-experts layer: https://arxiv.org/pdf/1701.06538.pdf,
Pathways: Asynchronous Distributed Dataflow for ML: https://arxiv.org/abs/2203.12533,

Qwen1.5-MoE: Matching 7B Model Performance with 1/3 Activated Parameters https://qwenlm.github.io/zh/blog/qwen-moe/

R. A. Jacobs, M. I. Jordan, S. J. Nowlan and G. E. Hinton, “Adaptive Mixtures of Local Experts,” in Neural Computation, 3, no. 1, pp. 79-87, March 1991, doi: 10.1162/neco.1991.3.1.79.

Roller, Stephen, Sainbayar Sukhbaatar, and Jason Weston. “Hash layers for large sparse models.” Advances in Neural mation Processing Systems 34 (2021): 17555-17566.

Sepp Hochreiter and Jürgen Schmidhuber. 1997. Long Short-Term Memory. Neural Comput. 9, 8 (November 15, 1997), 1735–1780. s://doi.org/10.1162/neco.1997.9.8.1735

Shazeer, Noam, et al. “Outrageously large neural networks: The sparsely-gated mixture-of-experts layer.” arXiv preprint v:1701.06538 (2017).

ST-MoE: Designing Stable and Transferable Sparse Expert Models https://arxiv.org/abs/2.08906

Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity https://arxiv.org/abs/1.03961

Tutel: Adaptive Mixture-of-Experts at Scale: https://arxiv.org/abs/2206.03382,

Vaswani, Ashish, et al. “Attention is all you need.” Advances in neural information processing systems 30 (2017).

Mixture-of-Experts with Expert Choice Routing（https://arxiv.org/abs/2202.09368）

MoE路由–expert choice routing Linsight

Auxiliary-Loss-Free Load Balancing Strategy for Mixture-of-Experts（https://arxiv.org/abs/2408.15664）

NeurIPS 2024 Oral | 小参数，大作为！揭秘非对称 LoRA 架构的高效性能机器之心

HydraLoRA: An Asymmetric LoRA Architecture for Efficient Fine-Tuning

https://arxiv.org/pdf/2501.00365

谈谈Llama4 和DeepSeek GRM zartbot