Deepseek Math （GRPO）论文解读

• 论文： https://arxiv.org/abs/2402.03300 （2024.02.05）
• 代码： https://github.com/deepseek-ai/DeepSeek-Math
• web： https://www.deepseek.com/

论文总结

DeepSeekMath 通过大规模数学预训练和高效强化学习（GRPO）算法，显著提升了开源模型的数学推理能力，在 MATH 基准上首次突破 50% 准确率，接近闭源模型水平。其方法论为开源社区提供了重要参考，未来在数据质量和算法效率上仍有优化空间。

1. 引言

1. 大型语言模型（LLM）的数学推理进展
   LLM在定量推理（如MATH基准）和几何推理任务中取得显著进步，同时辅助人类解决复杂数学问题。但闭源模型（如GPT-4、Gemini-Ultra）未公开，开源模型性能仍显著落后。

2. DeepSeekMath的目标与贡献
   提出DeepSeekMath，通过构建大规模数学语料库和优化算法，提升开源模型的数学推理能力，使其接近闭源模型水平。具体包括：

   • 开发DeepSeekMath Corpus（120B数学tokens），通过迭代筛选和去污染处理确保高质量；
   • 引入Group Relative Policy Optimization（GRPO），在减少训练资源消耗的同时提升数学推理能力；
   • 验证代码训练对数学推理的促进作用，并发现arXiv数据对基准任务无显著增益。

3. 模型优化流程
   DeepSeekMath-Base基于DeepSeek-Coder-Base-v1.5 7B初始化，通过数学预训练、监督微调和强化学习逐步优化，最终在MATH基准上达到51.7%准确率（GRPO优化后），超越所有开源模型。

2.Math Pre-Training

1. 数据收集与去污染
   • 迭代筛选管道：如 Figure2 所示，通过fastText分类器从Common Crawl筛选数学内容，结合人工标注优化模型，经过4轮迭代最终获得35.5M网页（120B tokens）。
   • 去污染处理：过滤包含基准数据（如GSM8K、MATH）的网页，确保训练数据不包含评估内容。

2. DeepSeekMath语料库特性
   • 高质量：如 Table 1 和 Figure 3 所示，在8个数学基准上，基于该语料库训练的模型性能显著优于MathPile、OpenWebMath等现有语料库。
   • 多语言覆盖：包含中英双语数学内容，提升中文数学任务表现（如CMATH准确率41.5%）。
   • 大规模：规模是Minerva所用数学网页的7倍，学习曲线更陡峭且持续提升。

3. 预训练模型训练与评估

   • 训练配置：基于DeepSeek-Coder-Base-v1.5 7B初始化，混合56%数学语料、20%代码、10%自然语言等数据，训练500B tokens。
   • 数学推理能力：如 Tabel 2所示，在MATH基准上达36.2%准确率，超越Minerva 540B（33.6%）及所有开源模型；工具使用场景下GSM8K+Python准确率66.9%。
   • 跨任务泛化：提升MMLU/BBH等语言理解任务表现，同时保持代码能力（HumanEval Pass@1达40.9%）。

4. 关键发现

   • 代码训练优势：代码预训练显著提升数学推理（尤其工具使用场景），验证代码对逻辑能力的促进作用。
   • arXiv无效性：单独使用arXiv数据对数学基准无显著增益，可能因内容结构差异导致。

3. Supervised Fine-Tuning

1. SFT数据构建

   • 构建776K数学指令数据集，涵盖中英双语问题，包含链上思维（CoT）、程序思维（PoT）和工具集成推理格式。
   • 英语数据来源包括GSM8K、MATH、MathInstruct等，覆盖代数、概率、几何等领域；中文数据覆盖K-12数学问题（76个子主题）。

2. 模型训练

   • DeepSeekMath-Instruct 7B基于DeepSeekMath-Base进行监督微调，使用4K上下文长度，训练500步，学习率5e-5，批量大小256。

3. 评估结果

   • 无工具推理：在MATH基准上准确率46.8%，超越所有开源模型（如WizardMath-7B的33.0%）及部分闭源模型（如Inflection-2、Gemini Pro）。
   • 工具集成推理：MATH准确率接近60%，超过10倍参数规模的DeepSeek-LLM-Chat 67B，展示小模型高效优化潜力。
   • 跨语言表现：在中文基准CMATH上达73.2%准确率，验证多语言数据有效性。

4. 关键结论

   • 监督微调显著提升模型的数学推理能力，尤其在复杂问题（如MATH）中表现突出，且工具集成进一步增强实用性。
   • 模型性能已接近闭源模型（如Gemini Ultra、GPT-4）水平，但仍有差距，需结合强化学习进一步优化。

4. Reinforcement Learning

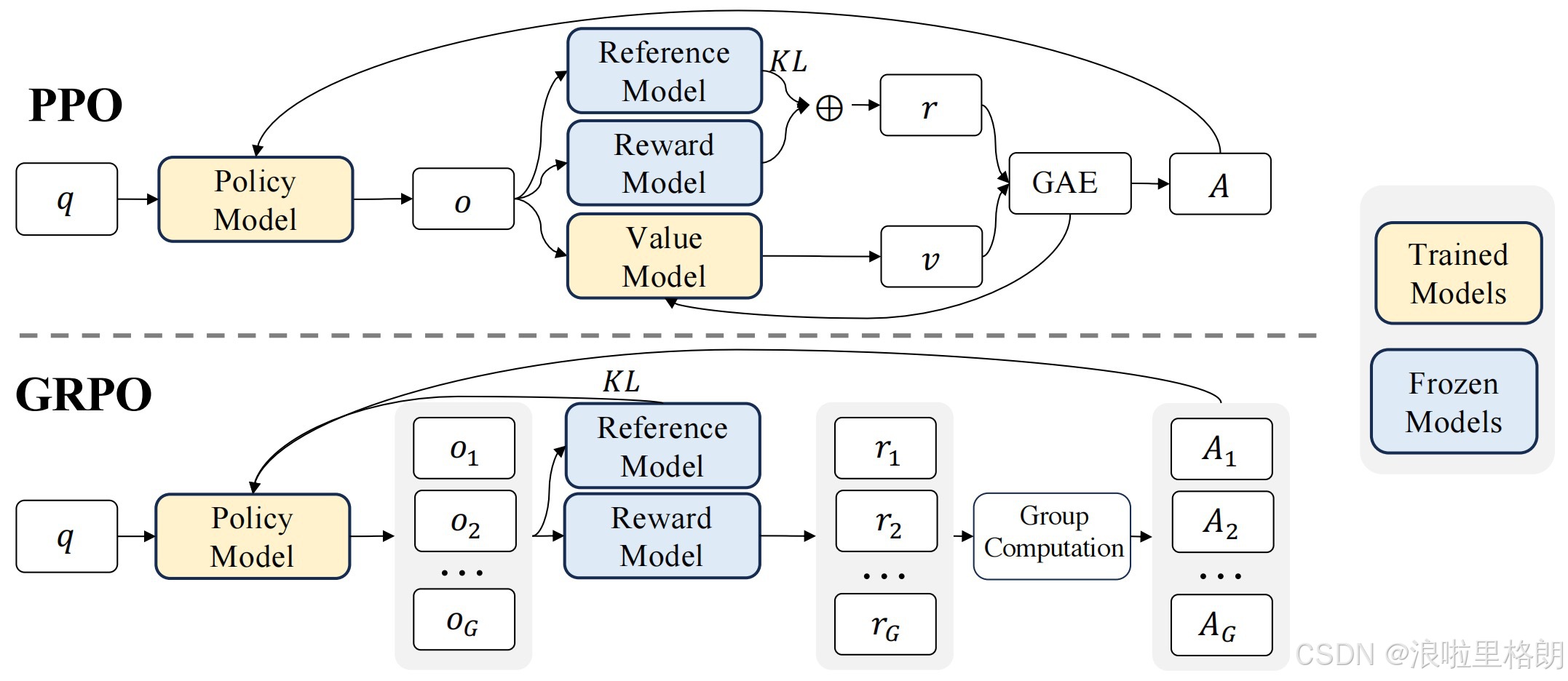
4.0 Proximal Policy Optimization (PPO)

核心思想：通过限制策略更新步长，平衡策略改进与稳定性。

关键组件：

1. 价值函数：估计状态价值 $V_{\psi }(q,o_{\le t})$，用于计算优势值。
2. 优势估计：
   $$A_t=r_{\ge t}-V_{\psi }(q,o_{\le t})$$
3. 奖励调整：
   $$r_t=r_{\phi }(q,o_{\le t})-\beta \log \frac{{\pi }_{\theta }(o_t)}{{\pi }_{\text{ref}}(o_t)}$$
   其中 $\beta$ 为KL惩罚系数。

目标函数：
$${\mathcal{J}}_{\text{PPO}}(\theta )=\mathbb{E}\left[q\sim P(Q),o\sim {\pi }_{{\theta }_{\text{old}}}(O|q)\right]\frac{1}{|o|}\sum _{t=1}^{|o|}\min \left(\frac{{\pi }_{\theta }(o_t)}{{\pi }_{{\theta }_{\text{old}}}(o_t)}{A}_t,\text{clip}(\cdot )\cdot A_t\right)$$

然而，PPO 的优势函数 $A_t$ 通常依赖于 Critic 模型（价值模型）估算状态值 $V(s_t)$，这带来了额外的计算开销。如果想要训练一个好的用于评价Actor模型的 Critic 模型，那么 Critic 模型必然不会比 Actor模型 小多少。

4.1 Group Relative Policy Optimization (GRPO)

核心目标：在减少训练资源消耗的同时，通过强化学习进一步提升模型的数学推理能力。

关键创新：

1. 省去价值函数：用组内奖励平均值作为基线，替代PPO中的价值函数。
2. 组相对优势估计：通过组内奖励标准化计算优势值，提升训练稳定性。
3. KL散度正则化：直接添加KL散度项，避免复杂奖励调整。

4.1.1 GRPO与PPO的对比

对比项	PPO	GRPO
基线估计	使用价值函数 $V_{\psi }$ 估计基线	使用组内奖励平均值 $\text{mean}(r)$ 作为基线
优势计算	$A_t=r_{\ge t}-V_{\psi }(q,o_{\le t})$	${\hat{A}}_{i,t}=\frac{r_i-\text{mean}(r)}{\text{std}(r)}$（结果监督）
奖励调整	奖励包含KL惩罚项 $r_t=r_{\phi }-\beta \log \frac{\pi }{{\pi }_{\text{ref}}}$	直接添加KL散度项到损失函数中
训练资源	需要训练价值函数（额外内存/计算）	仅需策略模型，资源消耗显著降低

4.1.2 GRPO数学公式

目标函数：
J GRPO ( θ ) = E [ q ∼ P ( Q ) , { o i } i = 1 G ∼ π θ old ( O ∣ q ) ] [ 1 G ∑ i = 1 G 1 ∣ o i ∣ ∑ t = 1 ∣ o i ∣ ( clip ( ⋅ ) ⋅ A ^ i , t − β D KL ) ] \mathcal{J}_{\text{GRPO}}(\theta) = \mathbb{E}\left[ q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(O|q) \right] \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left( \text{clip}(\cdot) \cdot \hat{A}_{i,t} - \beta \mathcal{D}_{\text{KL}} \right) \right] JGRPO​(θ)=E[q∼P(Q),{oi​}i=1G​∼πθold​​(O∣q)] ​G1​i=1∑G​∣oi​∣1​t=1∑∣oi​∣​(clip(⋅)⋅A^i,t​−βDKL​) ​
其中：

• ${\hat{A}}_{i,t}=\frac{r_i-\text{mean}(r)}{\text{std}(r)}$（结果监督）或 ${\sum }_{j\ge t}\frac{r_j^{\text{step}}-\text{mean}(R)}{\text{std}(R)}$（过程监督）。
• ${\mathcal{D}}_{\text{KL}}=\frac{{\pi }_{\text{ref}}(o_t)}{{\pi }_{\theta }(o_t)}-\log \frac{{\pi }_{\text{ref}}(o_t)}{{\pi }_{\theta }(o_t)}-1$（KL散度正则化）。

4.1.3 算法流程

1. 数据生成：

   • 对每个问题 $q$，从旧策略 ${\pi }_{{\theta }_{\text{old}}}$ 采样 $G$ 个输出 { o i } \{o_i\} {oi​}。
   • 使用奖励模型$r_{\phi }$ 为每个输出评分。

2. 优势计算：

   • 标准化奖励：${\tilde{r}}_i=\frac{r_i-\text{mean}(r)}{\text{std}(r)}$。
   • 优势值分配：所有token的优势值为 ${\hat{A}}_{i,t}={\tilde{r}}_i$（结果监督）。

3. 策略更新：

   • 最大化目标函数 ${\mathcal{J}}_{\text{GRPO}}(\theta )$，通过梯度下降优化策略模型 ${\pi }_{\theta }$。

4.1.4 关键实验结果

1. 结果监督 vs 过程监督：

   • 过程监督（逐步骤奖励）在MATH基准上提升更显著（51.7% vs 49.2%），但需要更多标注成本。

2. 迭代RL效果：

   • 两轮迭代后，MATH准确率从49.2%提升至51.7%（图6）。

3. 与其他方法对比：

   • GRPO在MATH上超越PPO、DPO等方法，且训练资源消耗更少（图5）。

4.2 统一范式分析

所有RL方法可统一表示为：
$${\nabla }_{\theta }\mathcal{J}=\mathbb{E}\left[(q,o)\sim \mathcal{D}\right]\left(\frac{1}{|o|}\sum _{t=1}^{|o|}{\text{GC}}_{\mathcal{A}}\cdot {\nabla }_{\theta }\log {\pi }_{\theta }(o_t|q,o_{<t})\right)$$
其中：

• GC（梯度系数）决定奖励信号的影响方式。
• 数据源（$\mathcal{D}$）分为离线（SFT数据）和在线（实时策略采样）。

方法	数据源	奖励类型	梯度系数（GC）
SFT	离线SFT数据	无	$1$（仅监督学习）
RFT	离线SFT采样	规则（正确/错误）	$\mathbb{I}(o)$（仅正确输出）
GRPO	在线策略采样	模型奖励	${\hat{A}}_{i,t}+\beta \left(\frac{{\pi }_{\text{ref}}}{{\pi }_{\theta }}-1\right)$

4.3 实验验证

1. 性能提升：

   • DeepSeekMath-RL 7B在MATH上达51.7%准确率，超越所有开源模型（包括70B参数模型），接近GPT-4（图1）。
   • 在CMATH中文基准上，准确率从73.2%提升至79.6%。

2. Maj@K vs Pass@K：

   • RL提升了Maj@K（多数投票准确率），但未显著提升Pass@K（单次正确概率），表明RL增强了输出分布的鲁棒性而非基础能力（图7）。

总结

GRPO通过组相对优势估计和KL散度正则化，在减少训练资源的同时显著提升数学推理能力。其在线训练和迭代优化机制为高效RL提供了新思路，未来可结合更复杂采样策略和抗噪声奖励模型进一步优化。

5. Discussion

5.1 Lessons Learnt in Pre-Training

1. 代码训练对数学推理的促进作用

   • 两阶段训练：先代码训练（400B tokens）再数学训练（150B tokens），显著提升工具使用场景下的数学推理能力（如GSM8K+Python准确率从12.4%提升至17.4%）。
   • 混合训练：同时包含代码和数学数据的单阶段训练，缓解灾难性遗忘问题，协同提升编程和数学能力（HumanEval Pass@1达29.3%）。

2. arXiv数据的无效性

   • 单独使用arXiv数据（MathPile或ArXiv-RedPajama）对数学基准无显著增益，甚至可能导致性能下降（如MATH准确率从3.0%降至2.2%）。
   • 推测原因：arXiv内容以学术论文为主，与基准任务的结构化数学问题不匹配。

5.2 Insights of Reinforcement Learning

1. 统一范式分析

   • 所有RL方法可统一表示为：
     $${\nabla }_{\theta }\mathcal{J}=\mathbb{E}\left[(q,o)\sim \mathcal{D}\right]\left(\frac{1}{|o|}\sum _{t=1}^{|o|}\text{GC}\cdot {\nabla }_{\theta }\log {\pi }_{\theta }(o_t|q,o_{<t})\right)$$
     其中关键组件包括：数据源（离线/在线）、奖励函数（规则/模型）、梯度系数（GC）。

2. 在线训练的优势

   • 在线RFT优于离线RFT（如MATH准确率提升2.5%），因实时策略采样能捕捉更复杂的数据分布差异。

3. GRPO的有效性

   • 通过组相对优势估计和KL散度正则化，GRPO在MATH上超越PPO（51.7% vs 49.2%），且训练资源消耗更少。

4. RL的作用机制

   • RL提升了Maj@K（多数投票准确率），但未显著提升Pass@K（单次正确概率），表明其增强了输出分布的鲁棒性而非基础能力（图7）。

5.3 Future Directions

1. 数据优化

   • 探索外部分布问题和树搜索解码策略，提升数据多样性。

2. 算法改进

   • 开发抗噪声奖励信号的RL算法（如Weak-to-Strong方法）。

3. 奖励函数优化

   • 增强奖励模型的泛化能力、不确定性建模及细粒度过程监督（如PRM800K数据集）。

关键结论

• 代码训练是提升数学推理的有效途径，但需合理设计训练策略。
• GRPO通过在线训练和组相对优势估计，在数学推理任务中实现高效优化。
• 未来需结合数据多样性、算法鲁棒性和奖励模型改进，进一步突破LLM的数学推理极限。